Posted on 9/02/2017

Resumo

Nesse estudo vamos mostrar a efetividade de uma rede neural para estimar a demanda por aluguel de bicicletas. Nós nos inspiramos livremente no experimento feito pelo time AzureML, onde os autores mostram a efetividade de engenhar novas variáveis para alavancar o poder preditivo de algoritmos de Aprendizado de Máquina Clássico. No nosso estudo, propomos uma alternativa com modelos de aprendizado de representações, no qual dispensamos completamente qualquer forma de engenharia de variáveis a mão e delegamos essa etapa do aprendizado à máquina.

Dados

Utilizaremos dados da companhia Capital Bikeshare, que opera serviços de aluguel de bicicletas na cidade de Washington DC, EUA. Os dados são públicos e podem ser encontrados aqui. Particularmente, utilizamos uma base de dados já tratada (Fanaee-T, Hadi, and Gama, Joao, 2013), que contém o registro de demanda a cada hora, totalizando 17389 observações ao longo dos anos de 2011 e 2012. Além dos registros de demanda, a base também traz informações meteorológicas do momento do registro e indicadores de dia útil ou feriado.

Trabalhos Relacionados

O presente estudo se baseia livremente no experimento Regression: Demand estimation, disponível na Cortana Intelligence Gallery. Nele, os autores criam um ensemble de Árvores de Decisão Impulsionadas para prever a demanda corrente por aluguel de bicicletas, utilizando a mesma base de dados citada acima. O time da Microsoft optou por utilizar o primeiro ano de registros (2011) como set de treinamento para o modelo, reservando as observações de 2012 para estimar o erro de generalização . Além disso, as variáveis categóricas foram codificadas como dummies. A partir daí, para mostrar a eficácia de engenharia de características, os autores montaram 4 bases de dados diferentes:

• A) A primeira base continha apenas as variáveis originais.

• B) A segunda base continha as variáveis originais mais a quantidade demandada em cada uma das últimas 12 horas.

• C) A terceira base continha as variáveis de A. e B. mais a demanda de cada um dos últimos 12 dias, para a mesma hora.

• D) A quarta base continha as variáveis de A., B. e C. mais a demanda de cada uma das últimas 12 semanas, para a mesma hora e durante o mesmo dia.

O mesmo modelo foi então treinado e testado em cada uma dessas quatro bases.

Métricas de Avaliação

Para avaliação, os autores utilizaram duas métricas de erro. A primeira delas é o erro absoluto médio, que pode ser entendido como a distância média entre o valor previsto e o valor real da demanda. Seja \( \hat{y} \) a demanda prevista e \( y \) a demanda observada, o erro absoluto médio é definido como:

\[EAM = \frac{1}{m} \sum{|\hat{y} - y|}\]

A segunda métrica utilizada foi a raiz quadrada do erro quadrático médio:

\[REQM = \sqrt{\frac{1}{m} \sum{(\hat{y} - y)^2}}\]

Os resultados obtidos foram os seguintes:

Base	EAM	REQM
A	89,7	124,9
B	51,7	88,3
C	47,6	81,1
D	48,3	82,1

O experimento pode ser integralmente conferido aqui.

Proposta

Ao contrário do estudo descrito acima, nossa proposta é dispensar qualquer tipo engenharia de características e ainda assim obter uma boa performance preditiva. Para isso, também vamos treinar um modelo com os dados de 2011 e utilizar os dados de 2012 para avaliação. Nós não realizamos nenhuma forma de engenharia de variáveis, nem sequer a codificação das variáveis categóricas para dummies.

Uma outra diferença notável entre o estudo aqui desenvolvido e o realizado pelo time AzureML é que, nesse último, utilizou-se as variáveis originais de uma hora para prever a demanda nesta mesma hora, ou seja, fez-se uma estimativa da demanda corrente a partir das variáveis correntes (no caso A.) e das variáveis passadas (nos outros casos). Na prática, estamos mais interessados em estimar a demanda futura a partir de variáveis correntes e passadas. Assim, nosso estudo propõe estimativas de demanda para diversas distâncias no futuro: 1 hora à frente, 12 horas à frente e 24 horas (um dia) à frente.

Aprendizado de Representações

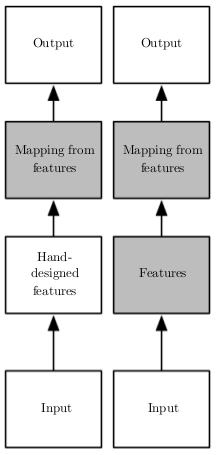
Em Aprendizado de Máquina Clássico, um problema que sempre aparece independente do algoritmo utilizado é que a tarefa mais difícil não é treinar a máquina, mas sim descobrir e engenhar novas variáveis que auxiliem no aprendizado. O estudo Regression: Demand estimation mostra como esse tipo de engenharia melhora o poder preditivo, mas há também que se considerar a enorme quantidade de esforço mental e tempo que geralmente é gasto nesse processo de pré-processamento dos dados.

Os modelos de Deep Learning surgem como forma de contornar esse problema: em vez de necessitarem de alguém para criar variáveis representativas manualmente, faz-se o uso de redes neurais profundas, que são capazes de aprendê-las sozinhas. Em distinção ao Aprendizado de Máquina Clássico, as redes neurais profundas fazem parte de um tipo de Aprendizado de Máquina, que leva o nome de aprendizado de representações. Com essas técnicas, além de aprender um mapeamento entre características representativas e um output desejado, a máquina consegue aprender as próprias características representativas de maneira automática.

Uma rede neural artificial profunda pode ser construída com aninhamentos sucessivos de diversas transformações lineares seguidas por alguma função não linear diferenciável, que é aplicada elemento a elemento da matriz de entrada. Seja \( \phi \) alguma transformação não linear (normalmente a função linear retificada, sigmóide ou tangente hiperbólica), a representação de uma rede neural profunda (com apenas duas camadas de profundidade) pode então ser descrita da seguinte forma:

\[\pmb{y} = \phi(\phi(\pmb{X}\pmb{W}_1)\pmb{W}_2)\pmb{w} + \pmb{\epsilon}\]

A parte \( \phi(\phi(\pmb{X}\pmb{W}_1)\pmb{W}_2) \) da rede neural é responsável por aprender as novas variáveis ou representações, que podemos denotar por \( \pmb{X^*} \). Em seguida, simplesmente utilizamos essas representações em conjunto com algum modelo linear:

\[\pmb{y} = \pmb{X^*}\pmb{w} + \pmb{\epsilon}\]

Uma outra forma de representar as redes neurais profundas é por meio de grafos, em que os dados entram por uma ponta e as previsões saem na outra:

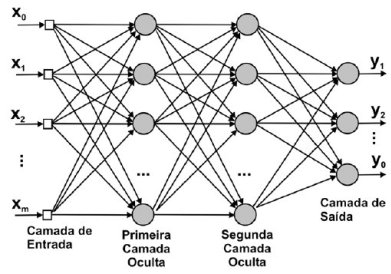
Podemos pensar nas diversas camadas ocultas de uma rede neural como aprendendo níveis de abstrações hierárquicos. Em reconhecimento de imagens, por exemplo, podemos pensar nas camadas mais baixas (próximas aos inputs) como aprendendo a detectar traços e variação de luminosidade, enquanto que as camadas superiores aprendem a juntar esses traços em partes de objeto. Essas partes então podem ser utilizadas por um modelo linear para discriminar entre um ou outro objeto. O tipo de rede neural descrito acima faz parte da classe de redes neurais feedforward densamente conectada. Nesse tipo de rede, todas as conexões são adiante, isto é, não há conexões que vão para a mesma camada ou para uma camada anterior. Além disso, a parte do nome ‘densamente conectada’ indica que cada variável de input à camada está conectada com cada neurônio da camada.

Redes Neurais e informação distribuída no tempo

Com uma arquitetura de redes neurais feedforward, cada observação dos dados flui de maneira independente pela rede. Portanto, não podemos esperar que esse tipo de rede consiga detectar que a demanda observada no passado possa ser um bom indicativo da demanda futura. Em termos mais técnicos, podemos dizer que as redes neurais feedforward densamente conectadas assumem que os dados são independentes e identicamente distribuídos (i.i.d.). Em séries temporais, como no nosso caso de estimação de demanda, isso certamente não é o caso, pois a demanda observada no passado é um ótimo indicador para a demanda observada no futuro. Em termos mais simples, podemos dizer que as redes neurais feedforward não tem nenhum mecanismo de memória.

Existem algumas formas de abordar esse problema e para entendê-las é preciso antes compreender como a informação temporal pode ser representada. Nós podemos pensar nesse tipo de informação como uma grade, na qual as colunas são as diferentes horas (ou períodos de tempo, no geral) e as linhas são as variáveis. O tempo então evolui da esquerda para a direita. Por exemplo, a representação em grade de três dias de informação pode ser vista na imagem a seguir, com cada linha representando uma variável:

Essas grades capturam toda a informação dos últimos 3 dias. Por exemplo, nas duas últimas linhas de cada imagem, vemos a demanda por pessoas cadastradas no sistemas e por usuários casuais, a cada hora. Podemos ver que há picos de demanda e se olharmos para a linha que representa as horas poderemos ver que esses picos acontecem no meio do dia e no fim da tarde, para usuários registrados e em dias úteis. Nós também podemos ver que a demanda de usuários casuais acontece principalmente nos dias de feriado (‘workingday’ marcado com preto) e praticamente desaparece nos dias úteis.

Com isso, nós poderemos agora achatar toda essa grade e alimentá-la como uma observação para a rede neural feedforward. Nós então procedemos normalmente, requerindo que a partir dessa grade de informação seja prevista uma demanda \( y \) em algum período futuro. Essa abordagem é a utilizada pela maioria dos modelos de econometria para séries temporais;  é o que chamamos de modelo autorregressivo,  pois nós utilizamos uma variável passada para prever a mesma variável no futuro, isto é, regredimos uma variável nela mesma.

Fazer uma rede neural autorregressiva faz com que ela capture informações do passado, mas não é uma solução muito elegante. Até porque, nós nos propomos a não realizar engenharia de variáveis e utilizar um modelo autorregressivo envolve criar novas variáveis com observações de diferentes passados. Em outras palavras, nós não estaríamos delegando à rede a tarefa de capturar automaticamente essa informação temporal. Há ainda um problema computacional de armazenagem, uma vez que redes neurais feedforward densas são muito abundante em parâmetros. Como temos 13 variáveis, se quisermos capturar apenas um dia (24 horas) de informação passada e utilizarmos apenas 10 neurônios na primeira camada oculta já teríamos 3120 (24x13x10) parâmetros para aprender; se quisermos utilizar 3 dias de informação e 100 neurônios, essa quantidade de parâmetros já sobe para 93600, apenas para a primeira camada!

Uma outra possibilidade, mais razoável, é utilizar redes neurais convolucionais, um tipo de rede neural feedforward que compartilha parâmetros e ainda induz um conhecimento a priori de que os dados estão organizados em grade. Com essas redes, é possível deslizar uma grade de neurônios (chamada kernel) ao longo da grade temporal. Essa grade de neurônios então observa diferentes locais da grade temporal, podendo detectar padrões de dependência entre um período e outro. Como os neurônios do kernel compartilham parâmetros, isso reduz de maneira drástica a quantidade deles que teremos de armazenar. (Para mais detalhes sobre o funcionamento desse tipo rede, favor verificar esta postagem).

Nós optaremos por uma terceira alternativa, que nós permite observar um hora de cada vez. Assim, em vez de apresentarmos à rede toda a grade de informação temporal, poderemos mostrar cada coluna (cada hora) individualmente. Isso resolve o problema de armazenagem, pois o tamanho do input à rede fica fixo no número de variáveis (no máximo 13 nesse caso), não dependendo mais do tamanho do horizonte temporal que queremos considerar. Além disso, não precisaremos realizar nenhuma engenharia de variáveis, pois bastará apresentar a rede um período temporal por vez e deixar que ela capture sozinha as dependências entre passado e futuro. Mas para isso, precisaremos abandonar a arquitetura feedforward da rede neural.

Redes Neurais Recorrentes

O nosso objetivo é, a partir de observações passadas, prever uma demanda futura. Seria então extremamente útil se pudéssemos ter algum mecanismo de memória na rede neural, de forma que ela consiga utilizar acontecimentos em diferentes níveis de passado para inferir sobre o futuro. Para isso, vamos utilizar uma rede neural recorrente (RNR), isto é, que tenha conexões que saem e levam de volta na mesma camada. Dessa forma, a rede consegue captar acontecimentos em períodos passados e redirecioná-los para o período que esta sendo processado no momento. Uma rede neural recorrente pode ser vista como uma rede neural feedforward muito profunda, que se desenrola no tempo:

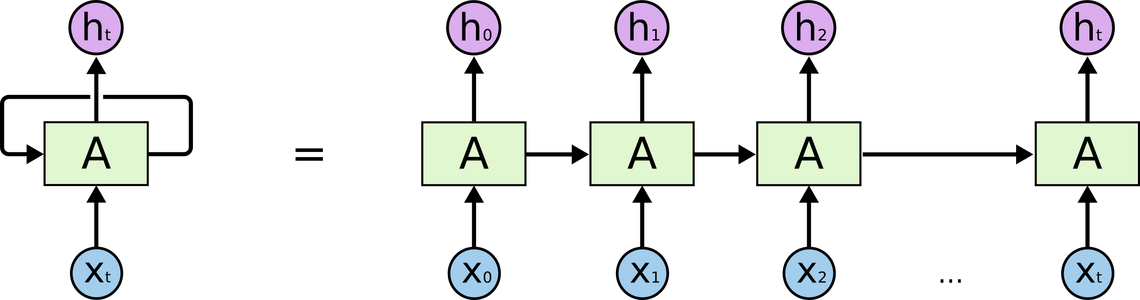
A cada período, a rede capta a informações correntes pelas conexões que levam dos inputs (X) à camada oculta (A). Além disso, por meio das conexões recorrentes, a rede consegue capturar a informação do que aconteceu nos períodos passados. Ao visualizar a RNR desenrolada no tempo, é preciso notar que os parâmetros que conectam passado e presente - os parâmetros da conexão recorrente - são sempre os mesmos. Isto significa que não há aumento de parâmetros a serem aprendidos se utilizarmos uma sequência temporal mais longa.

Redes neurais recorrentes são particularmente difíceis de treinar. Para sequências muito longas, é comum que a atualização dos parâmetros das conexões recorrentes se desvaneça em valores muito pequenos, fazendo com que a rede não consiga aprender informações de dependências mais remotas. Para possibilitar à RNR o aprendizado dessas dependências, é necessário substituir os neurônios tradicionais por alguma célula de memória. No presente estudo, utilizamos a célula LSTM (Long Short-Term Memory), que essencialmente dá a rede neural à possibilidade de escolher quando armazenar informação passada, quando esquecer a informação armazenada e quando utilizá-la para inferência.

O funcionamento dessas células de memória não é trivial, mas podemos dar uma explicação intuitiva de como a RNR funciona com e sem elas. Quando apresentamos uma amostra à rede neural recorrente, ocorre alguma atividade nos seus neurônios; nós podemos pensar nessas atividades como reverberações ou vibrações na camada oculta da rede. Quando então apresentamos a amostra seguinte na sequência, a rede ainda está vibrando com a amostra passada (essa vibração foi passada adiante pela conexão recorrente). Ela então precisa incorporar as vibrações produzidas pela observação atual às reverberações passadas. Sê não colocarmos nenhum mecanismo de memória, as reverberações passadas vão sendo dominadas pelas mais recentes e a rede esquece o que aconteceu num passado mais remoto. Com a utilização de células LSTM, a rede pode controlar quanto das vibrações passadas será levado adiante, quanto das vibrações correntes serão incorporadas à atividade da camada oculta e quanto das vibrações será passado adiante para produzir as previsões. Essa é uma intuição bem simples do que acontece de fato, mas bastará para compreender o funcionamento das RNRs com LSTMs. Para detalhes mais técnicos e precisos sobre o funcionamento de RNR com LSTM, sugerimos este artigo.

Também gostaríamos de enfatizar mais uma vez que redes neurais recorrentes não são modelos autorregressivos. Ao contrário desses modelos, as RNRs observam uma amostra por vez, e não uma sequência temporal inteira. Esse tipo de rede não pondera as diferentes observações passadas para produzir uma previsão para o futuro; elas aprendem a própria dinâmica evolução da sequência ao observar cada período no tempo individualmente e sucessivamente.

O Modelo

Nossa rede neural recorrente para previsão de demanda será o mais simples possível. Assim como na imagem acima, vamos utilizar apenas uma camada oculta entre os inputs e os outputs. O número de células nessa camada oculta será 256. Para agilizar o aprendizado, vamos limitar o tamanho da sequência temporal apresentada à rede para 3 dias (72 horas); após observar 72 horas sucessivas de demanda por aluguel de bicicleta, a rede neural fará uma previsão para a demanda futura. Nós então compararemos essa previsão com valor observado e minimizaremos a distância quadrada entre os dois. Formalmente, o modelo pode ser sintetizado na forma:

\[\pmb{h}_t = tanh(\pmb{W}_h \pmb{x}_t + \pmb{U}_h\pmb{h}_{t-1} + \pmb{b}_h)\] \[\pmb{y}_{t+n}=\pmb{W}_y \pmb{h}_t + \pmb{b}_y\]

• Em que \( \pmb{h}_t \) é o estado corrente da camada oculta;
• \( \pmb{x}_t \) são os inputs que a rede observa no momento;
• \( \pmb{W}_h \) e \( \pmb{b}_h \) são os parâmetros das conexões entre os inputs e a camada oculta;
•  \( \pmb{U}_t \) são os parâmetros das conexões recorrentes;
• \( \pmb{h}_{t-1} \) é o estado da camada oculta no período anterior;
• \( \pmb{W}_y \) e \( \pmb{b}_y \) são os parâmetros das conexões entre a camada oculta e o output.
• \( tanh \) é a função tangente hiperbólica.

Para treinar o modelo, utilizamos backpropagation através do tempo e o otimizador Adam, uma variação do algoritmo de Gradiente Descendente Estocástico, com taxa de aprendizado adaptativa e momento. Para o modelo que prevê a demanda uma hora adiante, foram realizadas 10 mil iterações de treino; para o modelo que prevê a demanda 12 e 24 horas a diante, foram realizadas 35 mil iterações de treino.

Resultados

Os resultados obtidos estão resumidos na tabela abaixo:

Horas à Frente	EAM	REQM
1	44,16	79,4
12	95,43	137,62
24	81,43	125,48

Em primeiro lugar, podemos notar que a performance da RNR para uma hora adiante é 3 pontos melhor do que a obtida pelo time AzureML, mesmo esse sendo um problema mais difícil (prever demanda futura). Isso mostra claramente como as redes neurais podem ser utilizadas em cenários de aprendizado de representações, onde seria preciso realizar engenharia de características caso se optasse por um algoritmo de Aprendizado de Máquina Clássico. Em segundo lugar, podemos notar que a previsão para 24 horas à frente é melhor do que a para 12 horas a frente. Esse comportamento pode nos dar alguma luz sobre o que está atravancando uma melhora da performance da RNR. Nós especulamos que a rede está utilizando principalmente dependências de curto prazo para realizar a previsão. Como a demanda 24 horas a diante acontece no mesmo período do dia da última observação disponível, a rede está conseguindo utilizar a dinâmica temporal da demanda naquele momento do dia para prever como será a demanda no dia seguinte. Quando pedimos para a rede representar uma demanda 12 horas a diante, elá terá de recorrer às dependências no mínimo 12 horas atrás para capturar a dinâmica temporal da demanda naquele período do dia.

Como a performance no set de treinamento é muito mais alta (EAM em torno de 20 em todos os casos), acreditamos que a rede está em um regime de super-ajustamento. Por isso, apenas as dependências recentes são suficientes para um bom resultado de treino, fazendo com que a RNR não aprenda as dependências de longo prazo. Nós não exploramos formas de sair desse regime para não contaminar o set de teste com múltiplas rodadas de avaliação. Além do mais, as redes neurais profundas normalmente precisam de muitos dados para se destacarem como algoritmo de Aprendizado de Máquina, mas temos mesno de 9000 observações de treino. Isso nos leva a pensar que seria extremamente complicado sair de um regime de super-ajustamento apenas com as técnicas de regularização ou diminuindo o tamanho do modelo. A implementação do que foi desenvolvido acima pode ser conferida no meu GitHub.