Posted on 20/02/2017
Conteúdo
Introdução
Utilizando dados do censo, vamos prever quais indivíduos tem renda maior do que 50 mil dólares anuais. No processo, nós vamos mostrar também o poder e a simplicidade de algoritmos lineares, comparando-o com outros algoritmos de aprendizado de máquina mais complexos. Particularmente, nós veremos que o algoritmo de regressão logística, mesmo sendo extremamente simples, consegue um performance igual ou apenas levemente inferior a de algoritmos não lineares e mais complexos.
Atenção! Este trabalho é uma adaptação do segundo projeto do Nanodegree Engenheiro de Machine Learning da Udacity. Se você está fazendo esse Nanodegree, saiba que uma série de sanções lhe podem ser aplicadas por submeter trabalho que não é seu. Assim, eu recomendo fortemente que não leia adiante antes de terminar o seu próprio projeto.
Os Dados
Os dados desse projeto são do censo americano de 1994. A base de dados foi retiradas do UCI Machine Learning Repository e foi compilada por Ronny Kohavi e Barry Becker. Após retirar alguns dados mal formatados ou com entradas ausentes, restaram 45222 observações. A variável que queremos prever é 'income' (renda), que assumo 1 se a renda do indivíduo for maior do que 50 mil dólares anuais e 0 caso contrário. Para informações detalhadas sobre as variáveis independentes utilizadas como preditoras, olhe a referência da base de dados.
Análise Exploratória
Antes de utilizar os modelos preditivos, conduzimos uma série exploração dos dados para melhor entender os padrões e relações neles presentes. Em primeiro lugar, nós descobrimos que apenas 24,78% dos indivíduos tem renda superior aos 50 mil dólares anuais, o que significa um modelo ingênuo que preveja sempre renda menor do que isso conseguirá uma acurácia de 75,22%.
Em seguida, nós procuramos entender a distribuição das variáveis contínuas. Nos nossos dados, existem apenas duas delas, 'capital-gain' (ganhos de capital) e 'capital-loss' (perdas de capital). Nós então montamos os histogramas de cada uma delas.
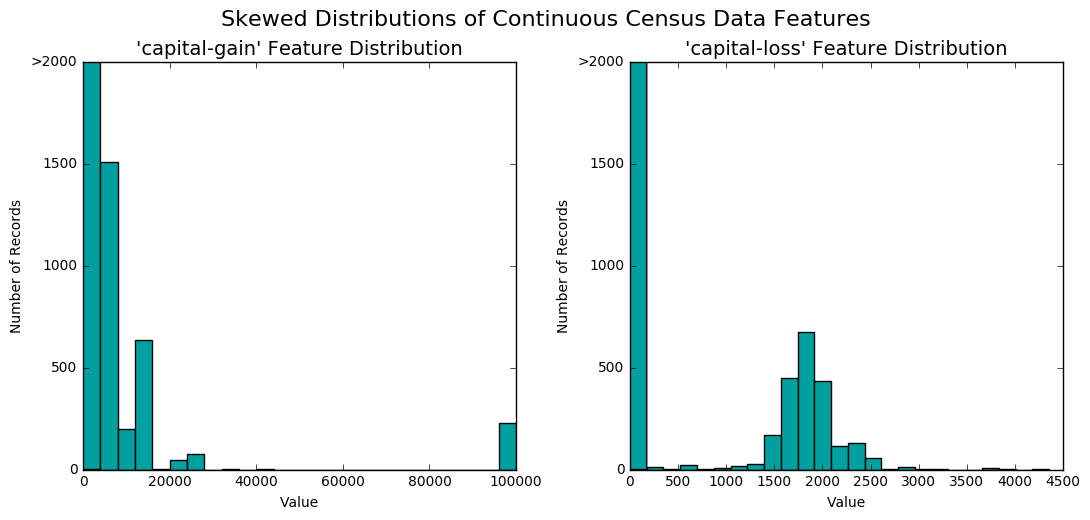
Nós notamos que as distribuições de ambas são bastante assimétricas e que maioria das pessoas não tem fonte de renda advinda de investimentos em capital (pois o valor com maior frequência tanto para ganhos quanto para perdas de capital é zero). Como algoritmos de aprendizado de máquina podem ser sensíveis a esse tipo de distribuição, nós aplicamos a transformação logarítmica nessas duas variáveis. Para evitar logaritmos de zeros (que são indefinidos), nós adicionamos 1 antes de aplicar a transformação. De forma resumida, nós substituímos as variáveis contínuas originais pelas suas versões transformadas da seguinte forma:
\[tranf (x) = log(x + 1)\]Após a transformação, os histogramas dessas variáveis assumiram o seguinte formato:
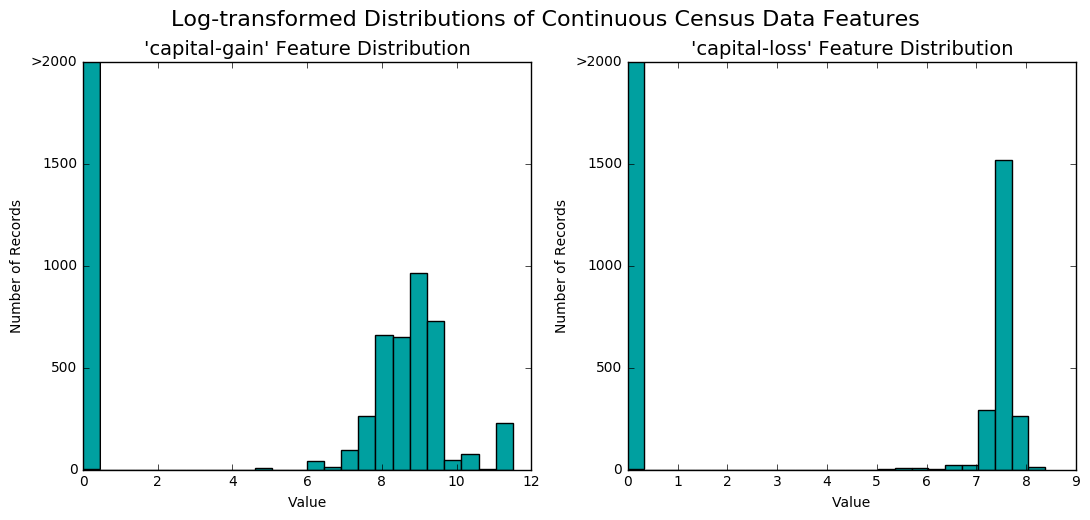
Em seguida, nós aplicamos escalonamento min-max em todas as variáveis numéricas, para que todas elas assumissem a mesma escala de valores, sendo assim tratadas igualmente pelos algoritmos de aprendizado de máquina, no início do treinamento. Por fim, nós codificamos as variáveis categóricas em dummies e separamos aleatoriamente um set de treino com 80% das amostras e o set de teste com o resto delas. Essa codificação final nos deixou com 103 variáveis, mas muitas delas esparsas, devido a codificação one-hot característica da transformação em dummies.</p>
Análise Inferencial
Métricas de Avaliação
Como já discutimos acima, mais de 75% dos indivíduos nos nossos dados recebem menos do que 50 mil dólares anuais. Em outras palavras, podemos dizer que as classes dos nossos dados estão desbalanceadas. Assim, utilizar apenas métrica de acurácia pode resultar em má interpretação da qualidade do modelo, uma vez que simplesmente prever sempre uma renda abaixo de 50 mil resultará em mais do que 75% de acurácia. Assim, nós vamos utilizar também uma outra métrica de avaliação, chamada F-score.
Para entender o F-score precisamos antes entender as métricas de precisão e revocação. A primeira delas nos dirá quanto dos indivíduos que prevemos como tendo renda maior do que 50 mil de fato tem renda maior do que 50 mil; a segunda métrica nos diz quando quanto dos indivíduos com renda superior a 50 mil nós conseguimos identificar como tendo renda superior a 50 mil. Formalmente, nós podemos definir essas métricas como sendo
\[P=\frac{T_p}{T_p + F_p} \quad \quad R=\frac{T_p}{T_p + F_n}\]Em que \( T_p\) são os verdadeiros positivos, \( F_p\) são os falsos positivos e \( F_n\) são os falsos negativos. De maneira intuitiva, a precisão nos penaliza caso classifiquemos muitas pessoas como alta renda, mas que são na verdade de baixa renda. A revocação, por outro lado, nos penaliza caso falhemos em identificar as pessoas de alta renda. Por exemplo, um classificador ingênuo que previsse baixa renda para todos os indivíduos obteria uma acurácia maior do que 75%, mas uma revocação de zero, pois não identificaria nenhuma pessoa de alta renda.
Por fim, o F-score é uma combinação dessas duas medidas e pode ser definido da seguinte maneira:
\[F_\beta = (1+\beta^2) \frac{P * R}{(\beta^2 * P) + R}\]Nesse caso particular, vamos utilizar \( \beta=0,5\) para dar mais ênfase à precisão.
Treinamento e Avaliação dos Modelos
Inicialmente, vamos treinar 3 classes de modelos off-the-shelf (prontos, com hiper-parâmetros padrões). O primeiro tipo de modelo será uma regressão logística, que é simplesmente um modelo linear para classificação. Explicações detalhadas sobre regressão logística e linearidade podem ser encontradas na seção de algoritmos deste site, nesta e nesta postagem, respectivamente. O segundo modelo considerado será uma árvore de decisão impulsionada. Por fim, consideraremos um modelo de k-vizinhos mais próximos. A grande diferença entre a regressão logística e os outros dois modelos considerados é que os últimos não estão restritos a aprender apenas relações lineares entre os dados. Em outras palavras, os dois últimos algoritmos considerados são aproximadores universais de qualquer função, o que significa que eles podem aprender as mais variadas formas de superfícies de separação entre os indivíduos de alta renda e os de baixa renda.
Nós treinamos os três modelos acima propostos e resumimos os resultados na seguinte imagem.

No primeiro quadro (superior, à esquerda), podemos ver o tempo de treinamento de cada modelo e logo notamos que a regressão logística é superior aos outros dois independente da quantidade de dados utilizada. Nos dois quadros seguintes (superior, ao centro e à direita), vemos que o modelo linear é apenas um pouco pior do que os outros, tanto em termos de acurácia quanto em termos de F-score, ambas as métricas medidas no set de treinamento. Nos quadros de baixo, primeiro podemos ver que o tempo para efetivar as previsões é negligenciável, tanto para o modelo de regressão logística quanto para o de árvore de decisão impulsionada. Em se tratando das performances avaliadas no set de teste, podemos ver que o modelo de árvore de decisão impulsionada é apenas marginalmente superior ao modelo linear e que este é, por sua vez, superior ao modelo de k-vizinhos mais próximos.
Resultados
Por fim, nós otimizamos o modelo de regressão logística com respeito ao seu hiper-parâmetro de regularização e os resultados foram resumidos na seguinte tabela.
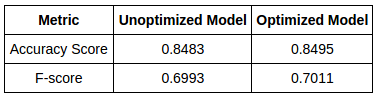
Podemos ver que a otimização resulta em pouca melhora. Isso acontece pelo fato de regressão logística já ser um modelo extremamente simples, no qual não há muito o que ajustar.
Referências
O projeto original pode ser conferido (em inglês) no meu GitHub. Além disso, na documentação do TensorFlow há um tutorial e uma discussão excelente sobre a resolução do mesmo problema abordado aqui.