Posted on 4/03/2017
Conteúdo
Introdução
Nós vamos avaliar cuidadosamente o poder preditivo de um modelo de Aprendizado de Máquina que foi treinado com dados de imóveis dos subúrbios de Boston, Massachusetts. Particularmente, vamos utilizar um modelo para prever o valor monetário do imóvel, mas nossa atenção será mais direcionada à forma como avaliaremos o modelo. Nós vamos trabalhar as noções de capacidade e generalização, abordando os problemas de viés e variância e mostrando a importância de validação cruzada. Para uma introdução a esses assuntos, veja a seção que fiz sobre capacidade e generalização em A. M. Essencial.
Atenção! Este trabalho é uma adaptação do primeiro projeto do Nanodegree Engenheiro de Machine Learning da Udacity. Se você está fazendo esse Nanodegree, saiba que uma série de sanções podem lhe ser aplicadas por submeter trabalho que não é seu. Assim, eu recomendo fortemente que não leia adiante antes de terminar o seu próprio projeto.
Os Dados
Os dados para esse projeto foram retirados do UCI Machine Learning Repository. A base original contém 506 observações agregadas sobre 14 variáveis de casas em diversos subúrbios da cidade de Boston. Os dados são referentes ao ano de 1978. Nesse projeto, foram mantidas apenas 4 variáveis:
- 'RM' é o número médio de cômodos por imóvel;
- 'LSTAT' é o percentual de proprietários na vizinhança considerados de 'classe baixa' (mais pobres);
- 'PTRATIO' é a proporção de estudantes por professores em escolas primárias e secundárias da vizinhança;
- 'MEDV' é o preço médio dos imóveis.
O nosso modelos irá prever 'MEDV' a partir das outras 3 variáveis. Durante o pré-processamento dos dados, 16 observações foram removidas por terem 'MEDV' de 50, indicando que esses dados estão corrompidos de alguma fora; uma observação foi removida por ter um 'RM' de 8,78, sendo assim considerada um outlier; a inflação de 'MEDV' foi corrigida para que os preços reflitam valores atuais, em dólares americanos.
Análise Exploratória
Em primeiro lugar, nós exploramos as estatísticas de 'MEDV' para entender melhor a distribuição da nossa variável alvo. Descobrimos que o valor médio era de US$ 454.342,94, o valor mínimo, US$ 105.000,00, o valor mediano, US$ 438.900,00 e o valor máximo, US$ 1.024.800,00. Além disso, o desvio padrão dos valores era de US$ 165.171,13.
Nós então prosseguimos com uma visualização da correlação entre as variáveis e da distribuição de cada uma delas (diagonal):
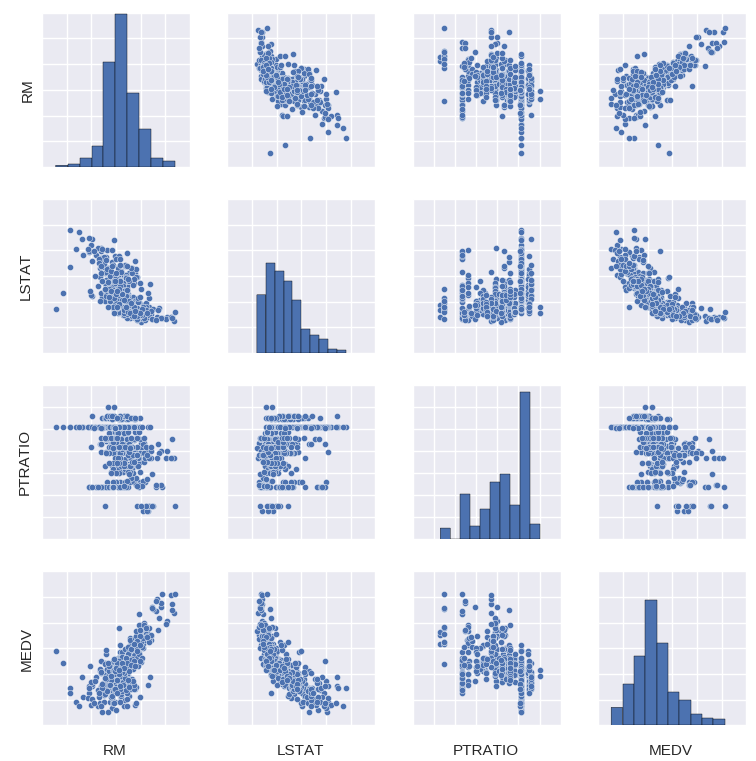
Para mais precisão, nós também produzimos a tabela de correlação entre as variáveis.
| RM | LSTAT | PTRATIO | MEDV | |
|---|---|---|---|---|
| RM | 1 | -0,612033 | -0.304559 | 0,697209 |
| LSTAT | - | 1 | 0,360445 | -0,760670 |
| PTRATIO | - | - | 1 | -0,519034 |
| MEDV | - | - | - | 1 |
Apenas com essas informações, já é possível tirar algumas conclusões interessantes sobre como o valor das casas se relaciona com cada variável. 'RM', por exemplo, pode ser vista como uma proxy para o tamanho das casas e, portanto, do seu custo de produção. Assim, é de se esperar que ela esteja positivamente correlacionada com o valor dos imóveis 'MEDV'. Por outro lado, 'LSTAT' pode ser vista como uma proxy para a pobreza da população. Como prevê a teoria microeconômica, renda e demanda estão negativamente correlacionadas, implicando que os preços de equilíbrio sejam mais baixos em vizinhanças de baixa renda, o que explica o fato de 'LSTAT' e 'MEDV' estarem negativamente correlacionadas. Por fim, podemos ver que 'PTRATIO' e 'MEDV' estão negativamente correlacionada. Isso se justifica se pensarmos em 'PTRATIO' como uma medida de qualidade da educação: quanto mais professores por aluno (menor 'PTRATIO'), melhores serão as escolas da vizinhança. Isso faz com que imóveis nessa vizinhança sejam mais demandados, o que explica o fato de 'PTRATIO' e 'MEDV' se moverem em direções opostas.
Análise Inferencial
Métrica de Avaliação
Como já dissemos, nosso foco aqui será na forma como avaliamos um modelo de Aprendizado de Máquina. Para tanto, é preciso que primeiro deixemos clara a métrica de performance que vamos utilizar. Como o problema que estamos lidando é de regressão (prever uma variável contínua), precisamos de uma métrica que esteja de acordo com esse tipo de problema. Por isso, nós vamos utilizar o coeficiente de determinação, ou \( R^2 \), para quantificar a performance do nosso modelo. O \( R^2 \) varia de o a 1, capturando a porcentagem de correlação entre a nossa previsão \( \hat{y} \) e o valor real \( y \). Um modelo cujo \( R^2 \) é zero é tão ruim quanto apenas prever sempre média de \( y \). Qualquer valor acima de 0 indica a porcentagem que \( \hat{y} \) é explicada pelo nosso modelo.
Formalmente, o \( R^2 \) é definido como:
\[R^2 = \frac{SSE}{SST} = 1-\frac{SSR}{SST}\]Onde
- Sendo \( \bar{y} \) a média de \( y \), \( SSE = \sum (\hat{y} - \bar{y})^2 \) é a soma dos quadrados explicada;
- \( SST = \sum (y - \bar{y})^2 \) é a soma dos quadrados total;
- \( SSR = \sum (\hat{u})^2 \) é a soma dos resíduos quadrados, em que \( \hat{u} = y - \hat{y} \).
Treinando e Avaliando os Modelos
Modelos de Aprendizado de Máquina podem ter uma capacidade arbitrariamente alta (dados recursos computacionais suficientes), o que os torna suscetíveis a aprender ruídos nos dados de treino como se eles fossem regularidades do processo gerador de dados. Como resultado, a performance do modelo medida com os dados utilizados para treiná-lo pode ser arbitrariamente alta. Esses modelos com alta capacidade costumam ter grande variância, pois aprendem padrões nos dados que são apenas resultado de aleatoriedade da amostra. Assim, quanto utilizamos esses modelos para prever dados não observados durante o treinamento, a performance deles cai consideravelmente, pois os padrões aleatórios aprendidos não mais estarão nessa nova amostra. Nós então dizemos que esses modelos não conseguem generalizar o que aprenderam.
Nós geralmente estamos interessados que nosso modelo seja bom em prever com dados não utilizados no treinamento. Em outras palavras, queremos que o nosso modelo tenha um baixo erro de generalização. Para ter uma estimativa do erro de generalização, nós separando os dados em três sets, um para treinar o modelo - o set de treino -, outro para ajustar a capacidade do modelo - o set de validação - e um último para avaliar o modelo - o set de teste. Nós vamos reservar 20% dos dados para estimar o erro de generalização e o resto para treinar o modelo. Como aqui temos poucos dados, vamos utilizar o mesmo set para validação e teste. Note que isso subestima o erro de generalização.
O modelo que vamos utilizar é uma árvore de decisão. Como o foco deste projeto é apenas a forma de avaliação de modelos de AM, não é necessário explicar detalhadamente o funcionamento desse modelo. Basta dizer que um dos hiper-parâmetros que ajusta a sua capacidade é a profundidade máxima da árvore, sendo que quanto maior essa profundidade, maior a capacidade do modelo.
A primeira forma de avaliação que vamos considerar é a curva de complexidade. Nós podemos entender a complexidade do modelo como um sinônimo da sua capacidade. Com uma grande capacidade, o modelo também é mais complexo, conseguindo assim aprender relações complexas nos dados. A curva de complexidade mostra como os erros no set de treino e as estimativas do erro de generalização evoluem com o aumento da capacidade/complexidade do modelo.
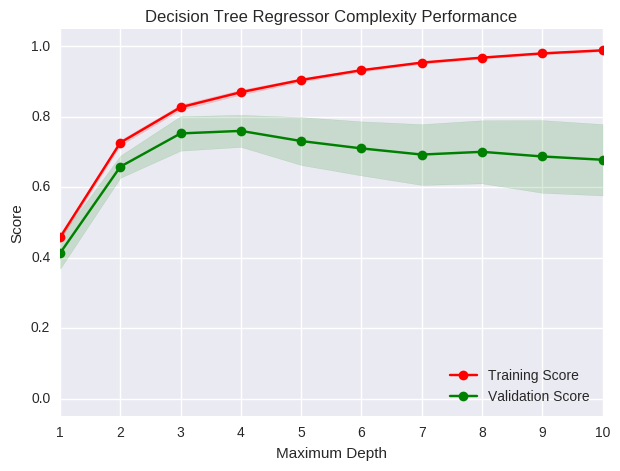
Lembre-se de que a profundidade máxima é um hiper-parâmetro de capacidade. Nós podemos ver que quando ela é muito baixa, o modelo não tem capacidade suficiente para aprender as regularidade nos dados. Nós dizemos que modelos desse tipo sofrem de alto viés e estão sub-ajustados. Por outro lado, quando a capacidade aumenta muito, o modelo começa a aprender ruído nos dados e passa a sofrer com alta variância, passando a ser super-ajustados. Nesse caso, o a performance no set de treino é quase perfeita, mas a estimativa da performance de generalização é baixa. Nós podemos utilizar a curva de complexidade para escolher a complexidade ótima para o nosso modelo: aquela nem tão alta, nem tão baixa, na qual o erro de generalização é menor.
Ao contrário do viés, o erro devido à variância pode ser diminuído com a utilização de mais dados de treinamento. Nós podemos ver isso com as curvas de aprendizado, que mostram como os erros de treino e generalização evoluem conforme utilizamos mais dados de treinamento.

Essas curvas nos dizem se coletar mais dados beneficiaria a performance de generalização do modelo. Quando o erro de treino e generalização estão próximo, coletar mais dados não beneficiaria a performance das nossas previsões; para isso, seria necessário aumentar a capacidade do nosso modelo. Por outro lado, se a performance de treino é mais alta do que a de generalização, recomenda-se coletar mais dados para treinar o modelo, até que o erro de generalização e treino convirjam.
Escolhendo o Melhor Modelo
Vimos que modelos muito complexos tendem a superajustar quando temos poucos dados, ao passo que modelos pouco complexos sofrem de sub-ajustamento. Isso mostra o tradeoff ente capacidade e generalização, um dos maiores desafios de qualquer praticante de Aprendizado de Máquina. Uma forma de confrontar esse tradeoff é utilizar validação cruzada k-fold e busca em grade pelos hiper-parâmetros.
A busca em grade de hiper-parâmetros realiza uma busca exaustiva pela melhor combinação de hiper-parâmetros e retorna aqueles que resultaram no melhor erro de validação. Para cada hiper-parâmetro, nós selecionamos um intervalo para explorar. Fazemos então um produto cartesiano de cada intervalo, para cada hiper-parâmetro e exploramos todos eles.
Nós podemos melhorar a busca em grade ao melhorarmos a técnica de validação cruzada. Na validação cruzada tradicional, quando simplesmente reservamos uma parte dos dados para treino e outra para avaliação, um problema que pode surgir é que a avaliação pode ter muita variância. Isso porque ela pode depender muito de quais observações foram para o set de treino e quais foram para o set de avaliação. Em outras palavras, a avaliação pode ser diferente dependendo de como a divisão dos dados é feita.
Com validação cruzada k-fold, nós primeiro separamos os dados em k sets diferentes e repetimos k experimentos de treino e avaliação, cada vez mantendo um sets diferente para avaliação. Por fim, tiramos a média das performances de validação dos k experimentos para obter uma estimação do erro de generalização. É importante notar que não existe uma estimativa não enviesada para tal erro (Bengio and Grandvalet, 2004), mas a aproximação obtida com validação cruzada k-fold é normalmente suficientemente boa. Outra vantagem dessa técnica é que cada observação será utilizada exatamente uma vez para validação, mitigando assim o tradeoff entre o tamanho do set de treino e de avaliação. Além disso, a variância da estimativa do erro de validação diminui conforme k aumenta (Alpaydın, 2014). Valores comuns de k são algo entre 5 e 10, mas isso é mais uma convenção prática do que uma regra.
Resultados
Utilizando as técnicas descritas acima, nós descobrimos que a complexidade ótima do nosso modelo é uma profundidade máxima de 4. Com esse hiper-parâmetro assim ajustado, conseguimos um \( R^2 \) no set de teste de 0,844, o que indica que nosso modelo explica 84,4% do valor dos imóveis.
Este projeto pode ser conferido (em ingles) no meu GitHub.