Posted on 12/03/2017

Redes neurais convolucionais são uma classe de modelos de Aprendizado de Máquina amplamente utilizada em problemas nos quais os dados estão organizados em grade, como séries temporais, análise de texto e reconhecimento de imagem. Nosso objetivo aqui é construir uma pequena rede neural convolucional para passar em um simples teste de Turing: o teste de Turing público completamente automatizado para diferenciação entre computadores e humanos, ou simplesmente CAPCHA. O texto desenvolvido abaixo é uma versão simplificada da explicação detalhada e bem mais técnica de como implementar este projeto. Essa versão mais detalhada pode ser conferida no meu GitHub.

Conteúdo

• A tarefa de enxergar
• Uma breve introdução às redes neurais
• Uma breve introdução às redes neurais convolucionais
• Uma rede neural convolucional para resolver CAPTCHAs
  • A natureza do problema
  • Os dados (X e y)
  • Considerações computacionais
  • Simulando os CAPTCHAs
  • Construindo o modelo de rede neural convolucional
  • Resultados
• Explorando mais fundo
  • Codificando a informação em abstrações
  • Decodificando as abstrações
• Referências

A tarefa de enxergar

No segundo episódio de Cosmos: A Spacetime Odyssey, Neil deGrasse Tyson nos mostra que o olho humano é tão mais complexo do que qualquer aparelho criado pelo homem, que inclusive já foi utilizado como argumento contra a teoria da evolução: como o acaso evolutivo poderia ter produzido algo tão elaborado? De fato, nós humanos somos tão bons em enxergar que ignoramos a verdadeira complexidade dessa tarefa: ao compreender uma imagem, temos que lidar com variações de luminosidade e ponto de vista, temos que segmentar a imagem em vários objetos e levar em conta a complexidade dos significados de cada um deles; em algumas cenas, precisamos detectar objetos parcialmente ocultos ou deformados, etc.

Para tornar essa tarefa mais fácil, nós humanos conseguimos ter noção de profundidade graças a habilidade de nos mover nas cenas que enxergamos e de termos desenvolvido visão binocular. No entanto, as imagens que gostaríamos que as máquinas reconhecessem são digitais, em 2D, e estáticas, tornando a tarefa ainda mais difícil. Mesmo assim, com a melhora da capacidade computacional e avanços nos algoritmos de inteligência artificial, já é possível treinar redes neurais que são melhores do que humanos em reconhecimento de imagens.

Uma breve introdução às redes neurais

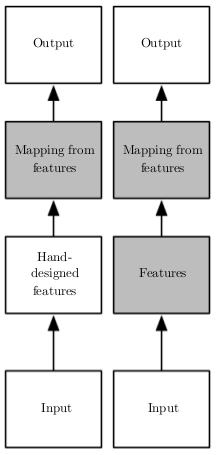
Em Aprendizado de Máquina clássico, um problema que sempre aparece, independente do algoritmo utilizado, é que a tarefa mais difícil não é treinar a máquina, mas sim, engenhar variáveis que auxiliem no aprendizado. Em reconhecimento de imagem, um exemplo de como isso acontece pode ser visto nos inúmeros e nada simples pré-processamentos que a imagem passa antes de ser alimentada a um algoritmo de Aprendizado de Máquina: filtros de ruído, segmentação, aumento de contraste, detecção de contornos, etc. As redes neurais artificiais (RNAs) surgem como forma de resolver esse problema: em vez de necessitarem de alguém para criar variáveis representativas manualmente, as redes neurais são capazes de aprendê-las sozinhas. Em distinção ao Aprendizado de Máquina clássico (imagem ao lado, coluna esquerda), as redes neurais são comumente utilizadas em um novo tipo de Aprendizado de Máquina, que leva o nome de aprendizado de representações ou Deep Learning (imagem ao lado, coluna direita), no qual além de aprender um mapeamento entre características representativas e um output desejado, a máquina consegue aprender as próprias características representativas de maneira automática.

Uma rede neural artificial profunda pode ser construída com aninhamentos sucessivos de diversas transformações lineares seguidas por alguma função não linear diferenciável, que é aplicada elemento a elemento da matriz de entrada. Seja \( \phi \) alguma transformação não linear (normalmente a função linear retificada, sigmóide ou tangente hiperbólica), a representação de uma rede neural profunda (com apenas duas camadas de profundidade) pode então ser descrita da seguinte forma:

\[\pmb{y} = \phi(\phi(\pmb{X}\pmb{W}_1)\pmb{W}_2)\pmb{w} + \pmb{\epsilon}\]

A parte \( \phi(\phi(\pmb{X}\pmb{W}_1)\pmb{W}_2) \) da rede neural é responsável por aprender as novas variáveis ou representações, que podemos denotar por \( \pmb{X^*} \). Em seguida, simplesmente utilizamos essas representações em conjunto com algum modelo linear:

\[\pmb{y} = \pmb{X^*}\pmb{w} + \pmb{\epsilon}\]

Uma outra forma de representar as redes neurais profundas é por meio de grafos, em que os dados entram por uma ponta e as previsões saem na outra:

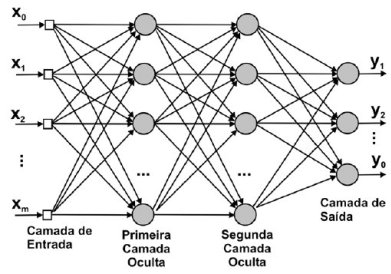
Podemos pensar nas diversas camadas ocultas de uma rede neural como aprendendo níveis de abstrações hierárquicos. Em reconhecimento de imagens, por exemplo, podemos pensar nas camadas mais baixas (próximas aos inputs) como aprendendo a detectar traços e variação de luminosidade, enquanto que as camadas superiores aprendem a juntar esses traços em partes de objetos. Essas partes então podem ser utilizadas por um modelo linear para discriminar entre um ou outro objeto.

É possível treinar uma rede neural da mesma forma que treinamos modelos lineares: contanto que saibamos diferenciar as funções de todas as camadas, poderemos propagar as derivadas de trás para frente com a regra da cadeia e utilizar gradiente descendente para aprender os parâmetros \( \pmb{W_i} \) de cada camada. No entanto, a superfície de custo de uma RNA é muito mais complexa do que a de um modelo linear, tornando o processo de treinamento muito mais demorado de difícil.

Uma breve introdução às redes neurais convolucionais

O modelo de RNA que descrevemos acima é chamado de totalmente conectado, ou denso, pois os neurônios de uma camada são conectados com todos os neurônios da camada seguinte. Esse tipo de rede neural é extremamente abundante em parâmetros, podendo gerar problemas de armazenamento na memória do computador. Por exemplo, considere o caso em que a matriz de entrada \( \pmb{X} \) contém imagens coloridas (RGB), com altura de 40 e largura de 140 px. Nesse caso, as colunas de \( \pmb{X} \) somariam 16800 dimensões (3x140x40). Se conectarmos à entrada uma pequena camada oculta, com apenas 10 neurônios, teríamos 168000 parâmetros \( \hat{w} \) para aprender, apenas na primeira camada!

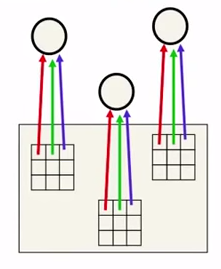
Ao fazer com que vários neurônios compartilhem o mesmo parâmetro \( \hat{w} \), as redes neurais convolucionais (RNC) se propõe a resolver esse tipo de problema. Além de diminuir o número de parâmetros, as RNC os estruturam de forma a induzir um conhecimento a priori de que os dados estão em formato de grade, como é o caso de imagens.

Na imagem ao lado, o compartilhamento dos mesmos parâmetros é demonstrado pela cor da seta, sendo ela a mesma para parâmetros compartilhados. Nós chamamos o quadriculado com os parâmetros de filtro, ou kernel da convolução. Podemos imaginar o kernel como um quadriculado que vai deslizando pela imagem, produzindo um output filtrado para a próxima camada. O output de cada local por onde o kernel passa forma um pixel do mapa representativo da imagem, que é então passado à próxima camada. Essa operação de deslizar uma grade de parâmetros pela imagem é chamada de convolução.

É comum utilizar após a convolução uma camada de agrupamento (pooling) dos pixeis, normalmente com um agrupamento de média ou máximo. A camada agrupamento também tem um kernel quadriculado, que passa pela imagem computando a função de agrupamento. Uma típica passagem de dados por uma rede convolucional pode ser vista a seguir:

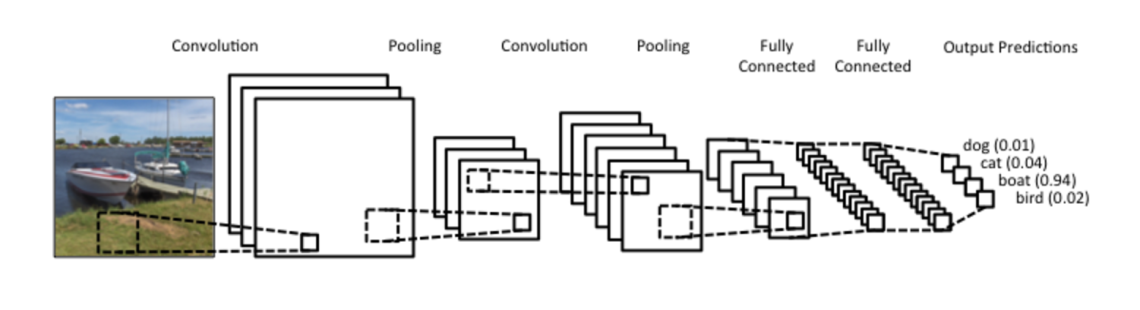
Normalmente, utilizam-se vários filtros  na camada de convolução. Nesse caso, diz-se que a profundidade do kernel é o número de filtros que utilizamos. Cada filtro produz uma imagem, ou melhor, um mapa de características da imagem. A forma empilhada desses mapas pode ser vista como uma imagem mais profunda. Por exemplo, podemos passar uma imagem de profundidade 3 (cores RGB) por uma camada convolucional com 16 filtros (ou um kernel de profundidade 16) e o output será um mapa de características com profundidade 16. É importante perceber que cada um desses filtros pode aprende a detectar um padrão diferente na imagem, e o procura ao longo dela.

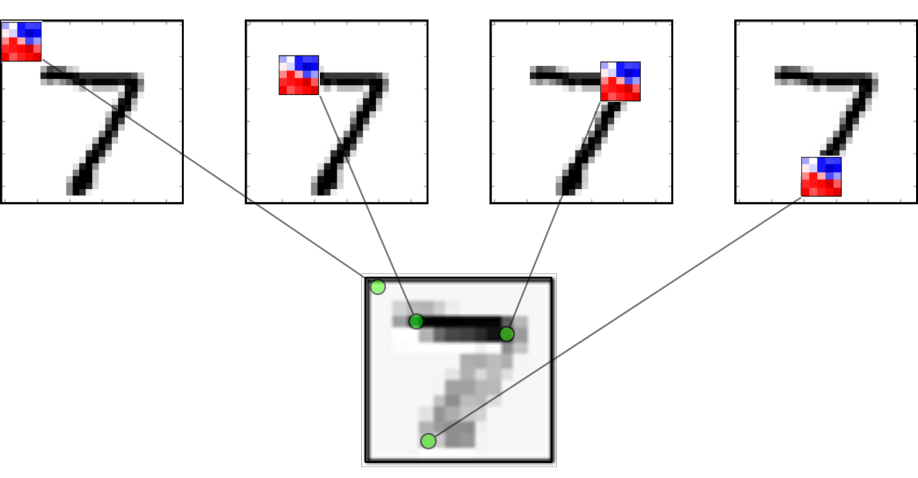
Redes neurais convolucionais são excelentes em detectar padrões em imagens pois elas conseguem aprender invariância do ponto de vista. Isto é, elas podem detectar o padrão, independente da posição dele na imagem, uma vez que o kernel passa por toda a imagem. É desejado que se parta de uma imagem larga e rasa no input da rede de se produza como output um mapa característico fino e profundo. Isso costuma aumentar o poder representativo da rede neural. É também comum adicionar ao final das camadas convolucionais uma ou duas camadas ocultas densas (ou completamente conectadas).

Uma rede neural convolucional para resolver CAPTCHAs

Uma vez que tenhamos explicado brevemente o funcionamento de redes neurais, passamos agora para a implementação de uma rede neural convolucional para resolver um simples teste de Turing. Nossa referência para resolver esse problema vem de um artigo publicado por Goodfellow et al, pela Google Inc., em 2014, no qual os autores propõe uma metodologia para reconhecimento de caracteres em imagens (OCR) que utiliza apenas uma rede neural convolucional. O modelo do artigo foi treinado na base SVHN, de números de casas coletados pelo Google Street View. Após treinada, a rede neural foi utilizada para numerar casas automaticamente. A apresentação do artigo pode ser conferida neste vídeo. A rede que treinaremos aqui será mais simples e menos profunda do que a do artigo, mas acreditamos que será suficiente para resolver os CAPTCHAs com uma boa acurácia (mais de 90%).

A natureza do problema

Nossa intenção é conseguir resolver CAPTCHAs automaticamente, isto é, sem intervenção humana. CAPTCHAs foram feitos exatamente para que essa tarefa não seja possível e são úteis para impedir que computadores naveguem livremente pela internet. O problema de resolver CAPTCHAs automaticamente pode ser visto sob a ótica de um problema de Aprendizado de Máquina Supervisionado, em que queremos mapear um input, nesse caso a imagem, em uma determinado alvo, nesse caso, a sequência de dígitos gravada na imagem. Por simplicidade, vamos nos referir aos inputs como \( \pmb{X} \), aos números na imagem como \( \pmb{y} \) e números previstos pela nossa rede neural como \( \pmb{\hat{y}} \). Matematicamente, nosso objetivo é minimizar a diferença entre \( \pmb{\hat{y}} \) e \( \pmb{y} \).

Os dados (X e y)

Os dados \( \pmb{X} \) serão um tensor de dimensões [tamanho_da_amostra, largura_da_imagem, profundidade_da_imagem]. Para conseguir identificar os CAPTCHAs, passaremos esses dados por uma rede neural convolucional. Antes disso, vamos redimensionar os CAPTCHAs para 32 x 96 px e convertê-los para preto e branco, reduzindo assim a profundidade da imagem para 1.

Os dados \( \pmb{y} \) precisarão de um pouco mais de processamento. No CAPTCHA, os números tem um valor categórico, de caractere, e precisamos codificá-los como tal. Para tanto, cada dígito do CAPTCHA será convertido em um vetor one-hot, em que todos os valores são zero e apenas a posição do dígito é marcada com 1. Esse vetor one-hot terá um tamanho de 11, podendo representar cada dígito mais a ausência de dígito ou dígito nulo. Como exemplos, o dígito '6' será codificado com um ‘1’ na sétima casa: [0,0,0,0,0,0,1,0,0,0,0]; o dígito '0' será codificado com um ‘1’ na primeira casa: [1,0,0,0,0,0,0,0,0,0,0]; o dígito 'nulo' será codificado com um ‘1’ na última cada casa: [0,0,0,0,0,0,0,0,0,0,1].

Vamos nos restringindo a um CAPTCHA com uma sequência de no máximo 6 dígitos. Por isso vamos empilhar 6 vetores one-hot para codificar a sequência toda do CAPTCHA. Dessa forma, \( \pmb{y} \) também será um tensor, dessa vez de dimensões [tamanho_da_amostra, tamanho_da_sequência=6, tamaho_do_vetor_one_hot=11]. Como exemplo, a sequência '142' seria codificada na forma:

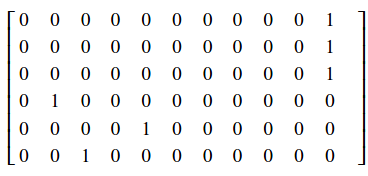
Considerações computacionais

Parra treinar a rede neural aqui proposta, utilizamos uma unidade de processamento gráfico GeForce GTX 1060 de 6GB. Além disso, o computador utilizado continha 16GB de RAM e um Intel i5. Para garantir a reprodutividade do que será desenvolvido adiante em computadores menos potentes, mantivemos o tamanho da rede neural relativamente pequeno e também restringimos o tamanho dos sets de teste e de validação. Nós testamos a possibilidade de treinar a rede do mesmo modo em um laptop com apenas 7GB de RAM e sem unidade de processamento gráfico, utilizando também um intel i5. Verificamos que menos de 5GB de RAM foram utilizados no processo de treinamento, o que garante sua reprodutividade da na maioria dos computadores modernos. Ainda assim, sem a utilização da unidade de processamento gráfico o treinamento torna-se bastante longo, demorando aproximadamente 5 minutos para rodar apenas 1000 iterações de treino e utilizando um mini-lotes de 50 exemplos cada.

Simulando os CAPTCHAs

Simulamos um set de treinamento com 50000 CAPTCHAs, um set de validação com 200 CAPTCHAs e um set de teste com 1000 CAPTCHAs. Após redimensionar as imagens, convertê-las para escala de cinza e aplicar um ruído aleatório para expansão artificial de dados, os CAPTCHAs simulados adquiriram a seguinte forma:

Esse é tipo de imagem que servirá de input a nossa rede neural. Note como há várias dificuldade para impedir o reconhecimento dos dígitos, como pequenos pontos de ruído, traços aleatórios, dígitos rotacionados e sobrepostos... Algumas são particularmente difíceis e provavelmente não seríamos capazes de distinguí-las se não tivéssemos acesso direto ao dígito que a gerou (mostrados embaixo das imagens). Na imagem do canto superior direito, por exemplo, note como o '7' é representado de maneira fina, parecendo apenas um dos traços de ruído; na imagem do centro, o '1' e 0 '7' são praticamente indistinguíveis. Não podemos ter certeza, mas acreditamos que a performance humana nesses CAPTCHAs não passe de 95%.

Construindo o modelo de rede neural convolucional

Faremos uma rede neural convolucional com 6 camadas ocultas, sendo as 3 primeiras convolucionais e as duas últimas densas. Em todas as camadas, a função de não linearidade será a ReLU. A arquitetura da nossa rede será a seguinte:

Camada	Mapa representativo	Kernel/Filtro
Entrada	imagem 32 x 96 x 1	-
Convolucional	mapa 32 x 96 x 8	Convolução 5x5, passada de 1 por 1
Agrupamento	mapa 16 x 48 x 8	Max 2x2, passada de 2 por 2
Convolucional	mapa 16 x 48 x 16	Convolução 5x5, passada de 1 por 1
Agrupamento	mapa 8 x 24 x16	Max 2x2, passada de 2 por 2
Convolucional	mapa 8 x 24 x 32	Convolução 5x5, passada de 1 por 1
Agrupamento	mapa 4 x 12 x 32	Max 2x2, passada de 2 por 2
Convolucional	mapa 4 x 12 x 64	Convolução 3x3, passada de 1 por 1
Agrupamento	mapa 2 x 6 x 64	Max 2x2, passada de 2 por 2
Densa	mapa 1 x 128	-
Dropout	mapa 1 x 128	-
Densa	mapa 1 x 64	-
Saída	escores 6 x 11	-

Entre as camadas densas, vamos destruir aleatoriamente 50% do fluxo de dados (dropout), forçando a rede a aprender redundâncias, prevenindo sobre-ajustamento e melhorando a generalização dos resultados. A camada de saída da nossa rede neural será um vetor de escores, chamado geralmente de logit. Para converter esses escores em probabilidades, vamos passá-los por uma função softmax.

Escolhemos como métrica de performance a acurácia, que é definida como a proporção de acertos. Nós vamos contabilizar um acerto apenas se a rede neural conseguir reconhecer todos os dígitos na imagem e a ordem em que eles aparecem. Portanto, não haverá melhora na pontuação por CAPTCHAs parcialmente desvendados. Durante o treinamento, vamos calcular a acurácia no set de validação a cada 1000 iterações de treino e salvar os parâmetros \( \pmb{W_{ij}} \) apenas nos momentos que houver melhora nessa acurácia.

Resultados

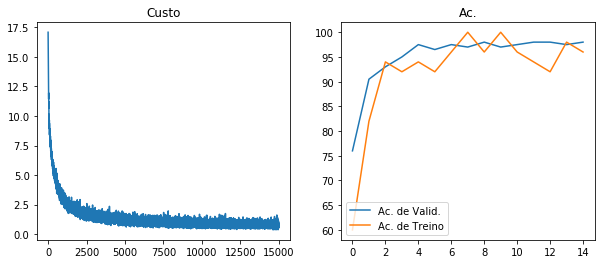
A rede neural implementada converge rapidamente, de forma que com apenas 2000 iterações de treino já consegue uma acurácia de validação de 90.5%. Nós treinamos a rede neural por 15000 iterações, o que nos deu uma acurácia de teste de 98.2%. Mais especificamente, apenas 18 dos 1000 CAPTCHAs de teste não foram identificados. Pela visualização da evolução do treinamento (imagem acima), temos razões para acreditar que a rede neural não foi treinada por tempo suficiente. Isso porque podemos ver que, no final do treinamento, a acurácia de treino ainda está baixa relativa à de validação, indicando que interrompemos o treinamento em um regime de sub-ajustamento. Contudo, nós optamos por manter o número de iterações de treino baixo, de modo a possibilitar uma reprodução não tão demorada desse projeto em computadores menos potentes. A seguir, selecionamos 9 CAPTCHAS ao acaso e visualizamos o valor previsto para cada um deles:

Podemos ver que a rede neural acertou todos os 9 CAPTCHAs selecionados, incluindo aqueles em que o '7' e o '1' são praticamente indistinguíveis. Nós também selecionamos ao acaso 9 dos 18 CAPTCHAs que a rede neural não conseguiu resolver. Nossa esperança era que, visualizando-os, pudéssemos entender melhor o motivo do erro. Abaixo estão esses 9 CAPTCHAs junto com a previsão produzida pela rede neural.

Notamos que algumas das imagens erradas estão com uma luminosidade bem fraca, o que pode ter causado a dificuldade em resolvê-las. No entanto, alguns dos CAPTCHAs acima  não apresentam nenhuma dificuldade aparente. Nossa hipótese para esses erros é que a rede neural não treinou por tempo o suficiente, mas isso é apenas uma especulação.

Explorando mais fundo: uma tentativa de entender as abstrações aprendidas pela RNA

Uma especulação sobre a forma como enxergamos é que precisamos formar abstrações semânticas dos estímulos visuais que recebemos, de forma que não somos capazes de enxergar o que não entendemos. Em outras palavras, podemos dizer que o processo de abstração é de duas vias: para aprender a enxergar é preciso abstrair e para abstrair é preciso aprender a enxergar. Algumas evidências apontam que essa especulação não é de todo infundada. Por exemplo, não conseguimos imaginar algo que ainda não existe, ou seja, não conseguimos abstrair uma imagem de um conceito que não nos é familiar.

Isso não passa de uma expeculação sobre a forma como nós enxergamos o mundo, mas em se tradando de redes neurais podemos ter certeza de que é assim que elas veem. Nas RNAs, podemos ter acesso direto às representações aprendidas, pois temos controle e acesso fácil a cada neurônio da rede. Com a nossa rede neural de CAPTCHAs, por exemplo, sabemos que a informação passa por várias camadas de neurônios, sendo que a última delas tem apenas 64. Esses 64 neurônios então precisam ser capazes de abstrair o conteúdo mais importante da imagem, de forma que seja possível classificá-la entre diversos dígitos. Em outras palavras, a rede neural precisa codificar informação de uma imagem com 3072 dimensões (32x96 pixeis) em apenas 64 neurônios de forma que essa representação reduzida seja representativa o suficiente para possibilitar a classificação dos dígitos.

Há toda uma literatura explorando formas de extrair essa representação interna da rede neural, mas não temos espaço para tratar de todas elas aqui. Vamos então utilizar uma abordagem bastante simples e bastante efetiva. Em primeiro lugar, nós precisamos entender que a última camada oculta da rede neural produz uma representação condensada da imagem que é suficiente para a tarefa de classificação. Nós vamos então tentar reverter esse processo, de forma que possamos chegar da representação condensada de volta na imagem. Em termos mais simples, nós vamos fazer uma rede neural artificial que imagine de volta os CAPTCHAs abstraídos pela rede neural de reconhecimento de dígitos. Nós poderemos então visualizar essas imaginação da mesma forma que vimos os CAPTCHAs: como figuras.

Codificando a informação em abstrações

O primeiro passo para visualizar as abstrações aprendidas pela rede neural é passar por ela nossos dados de treino e retirar a abstração produzida na última camada oculta. Isso nos dará o mapa representativo da imagem como visto pela última cada da rede. Como descrevemos na arquitetura utilizada, esse mapa tem apenas 64 neurônios. Como a rede neural teve sucesso ao realizar a tarefa de identificação de CAPTCHAs, nós podemos garantir que nesses 64 neurônios é mantida informação suficiente para a tarefa de classificação de dígitos. No entanto, essa representação está codificada em uma forma que não fará sentido para nós humanos.

Decodificando as abstrações

Para decodificar essas abstrações, nós vamos criar mais uma rede neural, bem menor do que a primeira. O objetivo dessa rede neural será, a partir das abstrações previamente codificadas, reproduzir a imagem que as geraram. Em termos matemáticos, chamando as imagens de \( \pmb{X} \), essa nova rede neural produzirá uma reconstrução \( \pmb{\hat{X}} \) de forma a minimizar a diferença entre a imagem e a reconstrução \( (\pmb{X} - \pmb{\hat{X}})(\pmb{X} - \pmb{\hat{X}})^T \). A arquitetura dessa rede será a seguinte:

Camada	Mapa representativo
Entrada	Abstração 1 x 64
Densa	Abstração 1 x 512
Densa	Abstração 1 x 1024
Saída	Reconstrução 32 x 96 x 1

Como não linearidade, utilizamos a função tangente hiperbólica em ambas as camadas densas. Utilizamos normalização do mini-lote,  uma taxa de aprendizado de 0.001 e treinamos a rede por 5000 iterações. Após o treinamento, podemos visualizar as decodificações das abstrações dos CAPTCHAs.

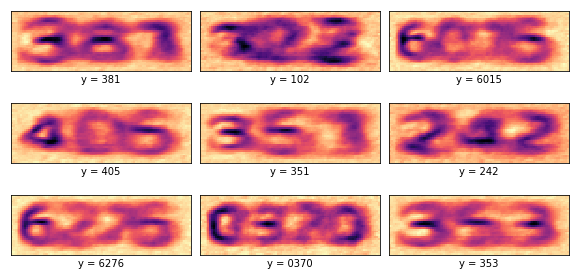
Podemos perceber como essas abstrações são extremamente úteis para identificação de dígitos. Elas parecem uma espécie de versão filtrada dos CAPTCHAs, onde todo o ruído foi retirado e também não há mais o risco que aparece por cima dos CAPTCHAs. Além disso, há traços mais escuros nos dígitos, sugerindo que essas formas são as mais características de cada um deles. Isso nos mostra como as RNAs de fato são capazes de aprender os conceitos que lhes ensinamos e fazem isso por meio dessas abstrações. Nesse caso, nossa RNA aprendeu bem os conceitos visuais de uma sequência de dígitos. Também podemos dizer que há um mecanismo de foco, que percebe algumas partes da imagem mais do que outras. Isso é extremamente similar à forma como nós humanos enxergamos as cenas, com atenção direcionada.

Referências

• Multi-digit Number Recognition from Street View Imagery using Deep Convolutional Neural Networks, Goodfellow et al, 2014.
• Deep Convolutional Networks, capítulo 9 do livro Deep Learning, por Goodfellow et al, 2016.
• Convolutional Neural Networks for Visual Recognition, Stanford.
• Neural Networks for Machine Learning, University of Toronto, por  Geoffrey Hinton.
• Machine Learning, 2014-2015, Oxford, por Nando de Freitas