Posted on 20/02/2017
Métodos iterativos de otimização são usados toda a parte de Aprendizado de Máquina. Aqui, nós vamos olhar o método de gradiente descendente. Em se tratando de uma simples regressão linear, o método de gradiente descendente só é recomendado quando temos dados com muitas dimensões. Nesse caso, a inversão da matriz \( \pmb{X}^T\pmb{X} \) começa a demorar muito e resolver regressão linear pela fórmula analítica \( \pmb{\hat{w}} = (\pmb{X}^T \pmb{X})^{-1} \pmb{X}^T \pmb{y} \) não vale mais a pena.
Nós também veremos um pouco de regimes de aprendizado online e em lotes (mini-batch learning) e discutiremos como esses regimes podem ser usados para aprender utilizando bases gigantescas, que não são possíveis de carregar de uma só vez para o RAM do computador (e.g. bases com +/- 20 GB).
Para melhor entendimento do algoritmo de otimização, é mais interessante começar usando-o em um problema mais simples, então vamos introduzir o algoritmo com um problema de regressão linear simples, com apenas uma variável na matriz de dados \( \pmb{X} \).
Conteúdo
- Pré-requisitos
- Intuição e explicação matemática
- Implementando e Visualizando gradiente descendente
- Hiper-parâmetros
- Problemas no aprendizado
- Gradiente descendente estocástico: aprendizado em mini-lotes
- Explorando melhorias: acelerando GDE
- Usando gradiente-descendente na prática
- Ligações-externas
Pré-requisitos
Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.
Intuição e explicação matemática
Vamos utilizar um exemplo de regressão linear bastante simples, com apenas uma variável dependente e uma independente. A relação entre elas pode ser expressa na equação \( \pmb{y} = b + \pmb{x} w + \pmb{\epsilon} \) e nós queremos achar os valores \( \hat{b} \) e \( \hat{w} \) que minimizam o quadrado da norma do vetor \( \pmb{\epsilon} \), isto é, minimizamos a soma dos quadrados dos resíduos.
A ideia pro trás dos métodos iterativos de otimização é bastante simples: nós começamos com algum chute razoável para os valores de \( \hat{b} \) e \( \hat{w} \) e vamos atualizando-os na direção certa até que chegamos no valor mínimo da nossa função custo, nesse caso, \( ||\pmb{\hat{\epsilon}}||^2 \). Matematicamente, nós temos que perceber que a nossa função custo, \( ||\pmb{\hat{\epsilon}}||^2 \), é uma função de \( \hat{b} \) e \( \hat{w} \):
\[\begin{aligned} L(\hat{b}, \hat{w}) &= ||\pmb{\hat{\epsilon}}||^2 \\&= \sum{\hat{\epsilon}}^2 \\&= \sum{(\hat{y}} - y)^2 \\&= \sum{(\hat{b} + x\hat{w}} - y)^2 \\&= (\pmb{X}\pmb{\hat{w}} -\pmb{y} )^T(\pmb{X}\pmb{\hat{w}} -\pmb{y} ) \end{aligned}\]Em que \( \pmb{\hat{w}} \) é o vetor com os parâmetros, incluindo \( \hat{b} \). Podemos minimizar essa função custo em seus parâmetros usando cálculo multivariado. Essa função custo - especifica de regressão linear - é uma função convexa, o que quer dizer que o único ponto de mínimo que ela tem é um mínimo global. Em outras palavras, a função custo pode ser vista como uma tigela, e o gradiente dessa função nos apontará a direção de descida mais íngreme, de forma que possamos chegar ao fundo da tigela, onde está o ponto de menor custo. No nosso exemplo com apenas dois parâmetros, essas direções são nos espaços de \( \hat{b} \) e \( \hat{w} \). Para implementar o gradiente descendente, basta atualizar simultaneamente os valores de \( \hat{b} \) e \( \hat{w} \), subtraindo deles as respectivas derivadas parciais da função custo, vezes uma taxa de aprendizado \( \alpha \) (o sinal \( := \) abaixo significa atualizar):
\[\hat{b} := \hat{b} - \alpha \frac{\partial}{\partial \hat{b}}L(\hat{b}, \hat{w})\] \[ \hat{w} := \hat{w} - \alpha \frac{\partial}{\partial \hat{w}}L(\hat{b}, \hat{w})\]Ou, no caso específico da nossa função custo de soma dos erros quadrados:
\[\hat{b} := \hat{b} - \alpha 2 \sum{(\hat{b} + \hat{w} x - y)}\] \[\hat{w} := \hat{w} - \alpha 2\sum{((\hat{b} + \hat{w} x - y) x)}\]Se quisermos simplificar, podemos retirar da fórmula \( 2 \) que não fará diferença, uma vez que as derivadas já estão sendo multiplicadas por uma constante \( \alpha \). Se quisermos simplificar a notação mais ainda, podemos utilizar a notação de vetores:
\[\pmb{\hat{w}} := \pmb{\hat{w}} - \alpha \nabla(L)\]No nosso caso, \( L(\pmb{\hat{w}} ) =(\pmb{X}\pmb{\hat{w}} -\pmb{y} )^T(\pmb{X}\pmb{\hat{w}} -\pmb{y} ) \) é a função custo e podemos achar o gradiente dela com cálculo de vetores:
\[\begin{aligned} \nabla(L) &= \frac{\partial}{\partial \pmb{\hat{w}}}(\pmb{X}\pmb{\hat{w}} -\pmb{y} )^T(\pmb{X}\pmb{\hat{w}} -\pmb{y} ) \\&= \frac{\partial}{\partial \pmb{\hat{w}}} (\pmb{\hat{w}}^T \pmb{X}^T \pmb{X} \pmb{\hat{w}} -2\pmb{\hat{w}}^T \pmb{X}^T \pmb{y} + \pmb{y}^T\pmb{y} ) \\&= 2 \pmb{X}^T \pmb{X} \pmb{\hat{w}} -2 \pmb{X}^T \pmb{y} \end{aligned}\]Em que \( \pmb{\hat{w}} \) é o vetor dos parâmetros da regressão linear, incluindo o intercepto \( \hat{b} \). Note que esse última regra de atualização é geral para qualquer número de dimensões que nossos dados possam ter.
E pronto. É só isso. Simples assim!
Implementando e Visualizando gradiente descendente
Para entender melhor como funciona o algoritmo de gradiente descendente, vamos simular alguns dados com uma relação conhecida, de forma que possamos ver o gradiente descendente em ação. Nós vamos trabalhar com uma regressão linear bem simples, com apenas dois parâmetros para aprender: o intercepto \( \hat{b} \) e a inclinação com respeito a única variável, \( \hat{w} \).
Particularmente, vamos gerar dados x e y de forma que \( y = 5 + 3x + \epsilon \), em que \( \epsilon \) é algum erro aleatório. Nós sabemos que os valores ótimos de \( \hat{w} \) e \( \hat{b} \) seriam então 3 e 2, respectivamente, então poderemos ver quão perto deles chegarão os parâmetros aprendidos por gradiente descendente.
Visualmente, se plotarmos os pares (x,y) teremos um gráfico como o abaixo. A nossa esperança é que a técnica de gradiente descendente consiga achar uma reta que melhor se encaixe nestes dados.
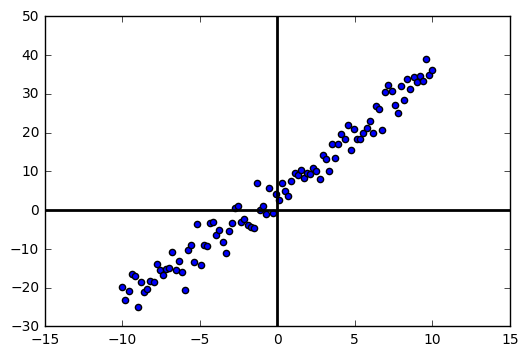
Antes de implementar a regressão linear por gradiente descendente, para melhor entendimento do algoritmo, é uma boa visualizar como é a nossa função custo quando plotada nas duas dimensões dos parâmetros \( \hat{b} \) e \( \hat{w} \) que queremos aprender:
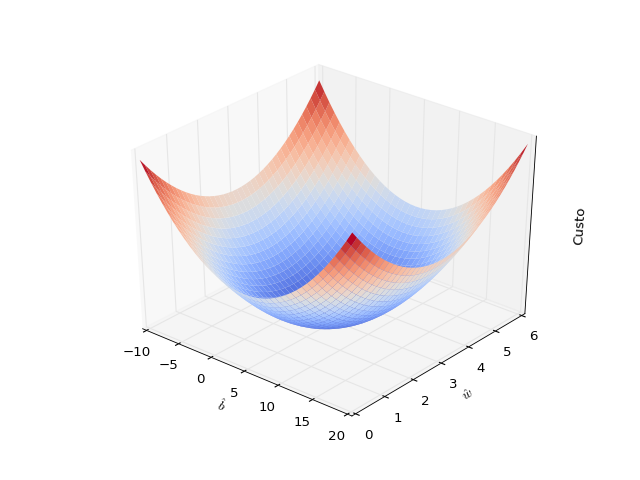
Como eu disse, a função de custo parece uma tigela. Se você olhar bem, vai perceber como o ponto de mínimo da tigela está onde \( \hat{b}=5 \) e \( \hat{w}=3 \). O gradiente dessa função é simplesmente um vetor de derivadas parciais, que dão a inclinação dessa tigela em cada ponto e em cada direção:
\[\nabla(L)=\Bigg[\frac{\partial L}{\partial \hat{b}}, \frac{\partial L}{\partial \hat{w}} \Bigg]\]Se nós seguirmos na direção oposta do gradiente, então chegaremos no ponto de mínimo. Podemos traçar uma analogia com uma bolinha de gude sendo solta em uma tigela: a bolinha descerá na direção mais inclinada e eventualmente parará no ponto mais baixo da tigela. Há uma importante diferença, no entanto. Quando falamos de uma bolinha de gude deslizando para o fundo de uma tigela, podemos visualizar a bolinha começando com uma pequena velocidade e acelerando ao longo do trajeto. Com gradiente descendente ocorre o oposto: inicialmente, os parâmetros \( \hat{b} \) e \( \hat{w} \) caminham rapidamente em direção ao ponto de mínimo e, quanto mais se aproximam dele, passam a caminhar cada vez mais devagar.
Mas por que isso acontece? Pense em como a cada iteração os parâmetros \( \hat{b} \) e \( \hat{w} \) dão um passo em direção ao mínimo. O tamanho desse passo será o valor do gradiente naquele ponto multiplicado pela constante \( \alpha \). Olhe de novo para o gráfico acima e note que quanto mais próximos estamos do ponto de mínimo, menor a inclinação da função custo, OU SEJA menor o gradiente, OU SEJA, menor o passo dado em direção ao mínimo.
Essa característica do método de gradiente descendente é ao mesmo tempo boa e ruim. É ruim pois atrasa o processo de aprendizado quando chegamos próximo do mínimo, mas é boa porque nos permite uma exploração mais minuciosa da superfície de custo em torno do ponto de mínimo. Dessa forma, podemos localizá-lo com mais precisão. Isso talvez não pareça muito importante nesse caso super simples de regressão linear com apenas dois parâmetros para aprender, mas quando estamos lidando com aprendizado de redes neurais com milhares de parâmetros e uma função custo não convexa você vai entender porque é importante essa exploração minuciosa do espaço da função custo.
Tendo dito tudo isso, vamos agora implementar a regressão linear com gradiente descendente. Note como abaixo nós nos restringimos ao caso simples para que possamos visualizar o processo de aprendizado. Algumas pequenas mudanças são necessárias no caso de uma regressão linear com vários parâmetros para aprender.
import pandas as pd
import numpy as np # para álgebra linear
np.random.seed(0) # para consistência nos resultados
dados = pd.DataFrame()
dados['x'] = np.linspace(-10,10,100)
dados['y'] = 5 + 3*dados['x'] + np.random.normal(0,3,100)
# define a função custo
def L(y, y_hat):
return ((y-y_hat) ** 2).sum()
# implementa regressão linear com gradiente descendente
class linear_regr(object):
def __init__(self, learning_rate=0.0001, training_iters=50):
self.learning_rate = learning_rate
self.training_iters = training_iters
def fit(self, X_train, y_train):
# formata os dados
if len(X_train.values.shape) < 2:
X = X_train.values.reshape(-1,1)
X = np.insert(X, 0, 1, 1)
# inicia os parâmetros com pequenos valores aleatórios
# (nosso chute razoável)
self.w_hat = np.random.normal(0,5, size = X[0].shape)
for _ in range(self.training_iters):
gradient = np.zeros(self.w_hat.shape) # inicia o gradiente
# computa o gradiente com informação de todos os pontos
for point, yi in zip(X, y_train):
gradient += (point * self.w_hat - yi) * point
# multiplica o gradiente pela taxa de aprendizado
gradient *= self.learning_rate
# atualiza os parâmetros
self.w_hat -= gradient
def predict(self, X_test):
# formata os dados
if len(X_test.values.shape) < 2:
X = X_test.values.reshape(-1,1)
X = np.insert(X, 0, 1, 1)
return np.dot(X, self.w_hat)
regr = linear_regr(learning_rate=0.0005, training_iters=30)
regr.fit(dados['x'], dados['y'])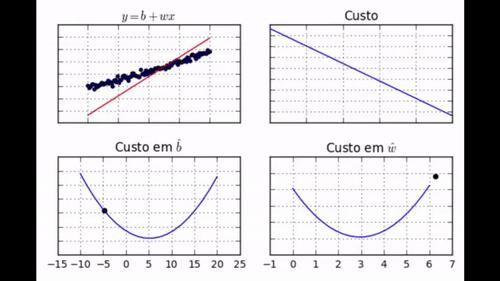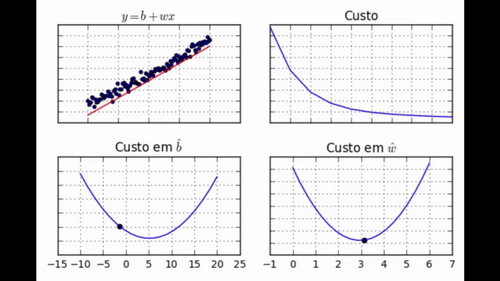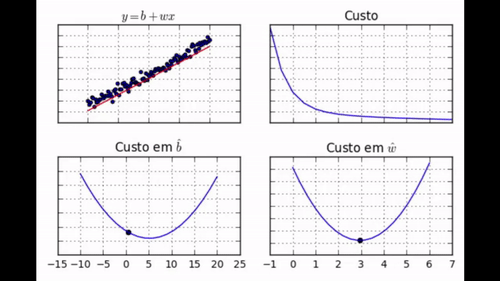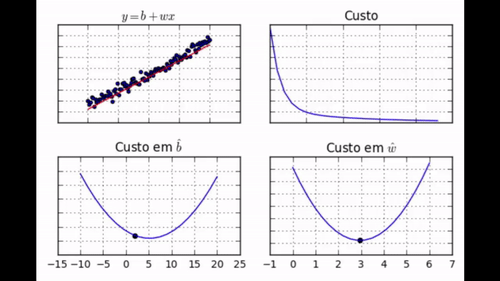
Nos GIF acima, você pode ver como evolui a posição da reta que queremos encaixar nos dados (gráfico 1), o custo (gráfico 2), o parâmetro \( \hat{b} \) (gráfico 3) e o parâmetro \( \hat{w} \) (gráfico 4). Note como com apenas 30 iterações de treino nós conseguimos que os parâmetros aprendidos chegassem muito perto dos valores de mínimo. Nós podemos dizer com confiança que nosso algoritmo de gradiente descendente foi um sucesso!
Obs: Para uma implementação com visualização do aprendizado, veja meu GitHub.
Hiper-parâmetros
O algoritmo de otimização iterativa por gradiente descendente é talvez o algoritmo de Aprendizado de Máquina mais importante que você vai aprender: ele é extremamente poderoso, relativamente rápido e funciona nos mais diversos cenários. No entanto, tudo isso vêm a um preço e nesse caso são os hiper-parâmetros.
Diferentemente dos parâmetros \( \pmb{\hat{w}} \), que são aprendidos durante o treinamento de uma regressão linear (ou de uma rede neural, como veremos mais para frente), os hiper-parâmetros não são aprendidos pela máquina durante o treinamento e devem ser ajustados manualmente. No caso da nossa regressão linear por gradiente descendente, podemos distinguir três hiper-parâmetros:
- A taxa de aprendizado
- O número de iterações de treino
- Os valores iniciais de \( \pmb{\hat{w}} \)
No caso de regressão linear, como a função custo é convexa, não importa muito onde começamos em termos de \( \pmb{\hat{w}} \). Se os outros dois hiper-parâmetros forem ajustados corretamente, chegaremos no mínimo independentemente do ponto de partida. Então, aqui nós não vamos dar muita atenção aos valores iniciais de \( \pmb{\hat{w}} \) (note como na nossa implementação eles nem sequer foram feitos para serem ajustados e são simplesmente pequenos valores aleatórios).
Agora, os dois primeiros hiper-parâmetros são muito importantes e o sucesso ou fracasso do aprendizado depende severamente de conseguirmos ajustá-los corretamente. A taxa de aprendizado é definitivamente o mais importante de todos, então vamos gastar um certo tempo discutindo como ela influencia no aprendizado e como ajustá-la bem.
A taxa de aprendizado define o tamanho dos passos que daremos em direção ao mínimo em cada iteração. Se esses passos forem muito pequenos, é quase garantido que chegaremos ao ponto de mínimo da função, mas para isso talvez precisaremos de muitas iterações de treino, tornando o algoritmo desnecessariamente lento.
Por outro lado, se colocarmos uma taxa de aprendizado muito alta, pode acontecer de sermos catapultados para cima da função custo e irmos cada vez mais longe do mínimo, resultando em uma falha completa de aprendizado. Isso acontecerá quando o passo que dermos for tão grande que pulará o ponto de mínimo e chegará em um ponto na função custo mais alto do que o de onde saímos. Nesse novo ponto, o gradiente será ainda maior, aumentando mais ainda o passo seguinte e nos arremessando ainda mais longe do ponto de mínimo a cada iteração.
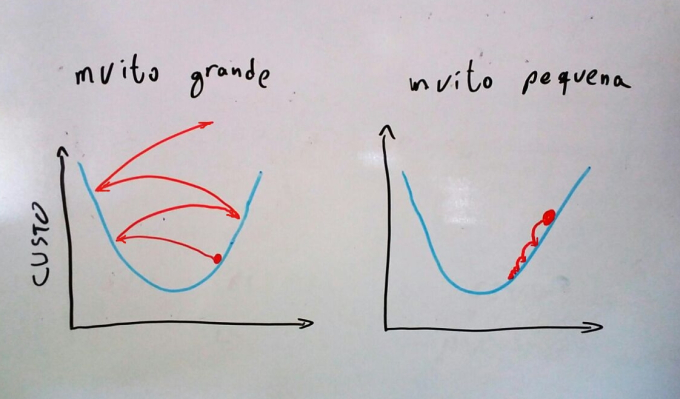
Podemos ver que a taxa de aprendizado não deve ser nem tão grande, nem tão pequena. Uma sugestão de ajustamento desse hiper-parâmetro é começar com 0.01 e explorar os pontos em volta dez vezes maior/menor (isto é, 0.1 e 0.001). Na maioria dos casos, uma boa taxa de aprendizado será algum dos seguintes valores: 1, 0.1, 0.01, 0.001, 0.0001, 0.00001.
Com uma boa taxa de aprendizado, selecionar o número de iterações de treino é uma tarefa fácil. Mesmo assim, recomenda-se plotar o valor da função custo a cada iteração de treino, assim como fizemos no gráfico 2 do GIF acima. Dessa forma você poderá ver se a função custo já chegou em uma região em que o seu valor não diminui ou diminui pouco a cada iteração.
No nosso caso, o gráfico da função custo a cada iteração é bastante suave, mas pode acontecer de haver tanto iterações em que o custo cai quando iterações em que o custo sobe. Se esse é o caso e a função custo flutua muito a cada iteração, recomenda-se diminuir a taxa de aprendizado. Se a função custo desce suavemente e constantemente, mas muito devagar, recomenda-se aumentar a taxa de aprendizado.
Problemas no aprendizado
Lembre-se de como a função custo da regressão linear é uma tigela? Se fizermos secções horizontais nessa tigela teremos um mapa topográfico da superfície de custo, assim como no ótimo desenho abaixo feito por mim.
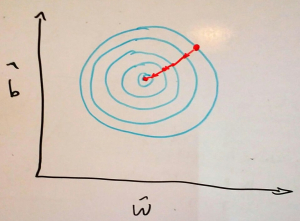
Sabemos que a otimização por gradiente descendente dará passos na direção mais inclinada, ou seja, na direção perpendicular as curvas de nível, assim como desenhado acima. Se as curvas de nível forem círculos perfeitos (como os que eu tentei desenhar), gradiente descendente só dará passos em direção ao ponto de mínimo e convergirá rapidamente. Por outro lado, se as curvas de nível da superfície de custo forem elipses alongadas, o tempo de convergência dependerá fortemente da inicialização dos nossos parâmetros.
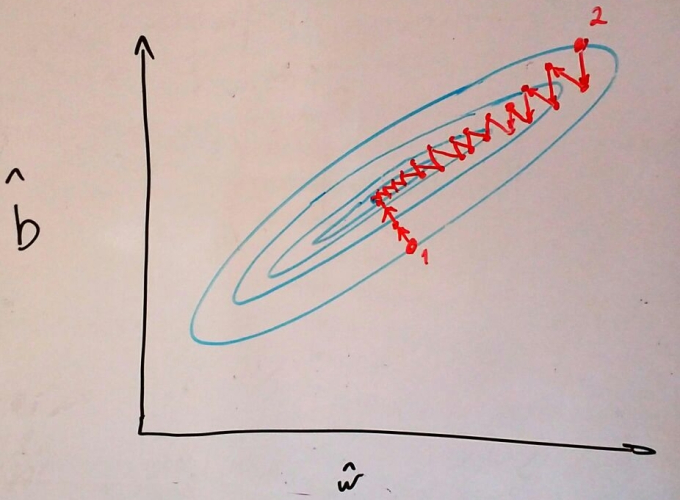
Por exemplo, se começarmos nossa descida no ponto 2 da imagem acima, a direção perpendicular à curva de nível aponta diretamente para o ponto de mínimo e não teremos maiores problemas durante o aprendizado. Mas se começarmos em um ponto como o 1 da imagem acima, a direção perpendicular à curva de nível aponta numa direção quase 90 graus da direção ao ponto de mínimo. Como consequência, daremos muitos passos em zig-zag e a convergência demorará muito mais.
Esse formato de elipse da função custo surge quando as variáveis dos nossos dados estão em escalas muito diferentes. Assim, uma solução simples para esse problema é deixar todos as variáveis na mesma escala. Uma forma de realizar isso é, para cada variável, subtrair a média e dividir pelo desvio padrão (normalização).
Gradiente descendente estocástico: aprendizado em mini-lotes
No exemplo simples que estamos usando, simulamos apenas 100 dados. Mas imagine agora que você deseja trabalhar com dados de algum censo, em que teremos observações na ordem de dezenas de milhões. Em primeiro lugar, você provavelmente não teria memória RAM suficiente para carregar todos os dados de uma vez, mas vamos supor que isso não seja um problema e você consiga implementar facilmente um procedimento que carrega os dados por partes. Você então inicia os parâmetros da regressão linear e agora precisaria percorrer todos os milhões de dados para computar o gradiente e dar apenas um passo da otimização. Em outras palavras, cada passo da otimização por gradiente descendente demora linearmente mais conforme mais dados temos. Isso é muito ineficiente e há uma forma muito mais rápida de realizar essa otimização.
Em primeiro lugar, considere se os seus dados tem alguma redundância, isto é, se você embaralhasse todas as observações, uma parte dos dados seria parecida com a outra? Se sim, então nós não precisamos percorrer todos os dados para computar o gradiente e podemos conseguir uma aproximação dele apenas olhando alguns exemplos dos dados. Essa é a ideia central por trás da técnica de gradiente descendente estocástico (G.D.E.).
Para possibilitar que a otimização por gradiente descendente continue rápida mesmo com milhões de dados, nós vamos alterá-la da seguinte forma:
- Primeiro, embaralhamos os nossos dados de forma que se retirássemos diferentes sub-amostras deles, elas não diferirão muito.
- Em segundo lugar, ao invés de computar o gradiente usando todos os dados, nós vamos fazer uma estimação dele usando apenas alguns dados - digamos um lote de 5 observações. Nós então atualizaremos os parâmetros com base nessa estimação do gradiente. Na atualização seguinte, nós repetiremos esse processo, mas agora estimando o gradiente com o próximo lote de dados, e assim por diante.
Você pode estar pensando que utilizar apenas 5 observações para estimar um gradiente nos dará uma estimativa bem ruim e você tem razão. Na verdade, essa estimativa é tão ruim que muitas vezes o gradiente estimado nos levará em uma direção errada e custo aumentará. No entanto, na média, o gradiente estimado nos levará na direção correta. Em resumo, com GDE precisaremos de mais iterações de treino para chegar próximo do mínimo, mas cada iteração demorará muito (muuuito, muuutio) menos tempo e o aprendizado como um todo será mais rápido. A rigor, se gradiente descendente com todos os dados demora linearmente mais conforme mais dados temos, com GDE o tempo de treino é CONSTANTE e não aumenta com o a quantidade de dados! Você leu direito! Isso porque pode acontecer de nem sequer precisarmos ver todas as observações para chegar a uma região razoável na função de custo.
Mais ainda, como não precisamos de todos os dados de uma vez para o processo de treinamento, podemos utilizar essa técnicas para Aprendizado de Máquina em bases de dados gigantescas, maiores até do que nosso computador suportaria trazer para a memória de curto prazo de uma só vez (digamos, bases com mais de 100GB).
Ao utilizar GDE introduzimos mais um hiper-parâmetro que terá que ser ajustado manualmente: o tamanho do lote. É importante entender como esse hiper-parâmetro funciona para saber como ajustá-lo bem. Em geral, lotes maiores significam passos mais precisos em direção ao mínimo, mas ao mesmo tempo significa passos mais demorados. Não existe uma recomendação única para o tamanho do mini-lote pois o tamanho ótimo depende fortemente da característica dos dados em questão. Se os dados são bastante redundantes, um mini-lote menor bastará, mas se os dados forem muito desbalanceados, recomenda-se usar um mini-lote maior. Normalmente o tamanho do mini-lote varia entre 1 a 1000 observações, mas podem surgir ocasiões que peçam um mini-lote maior.
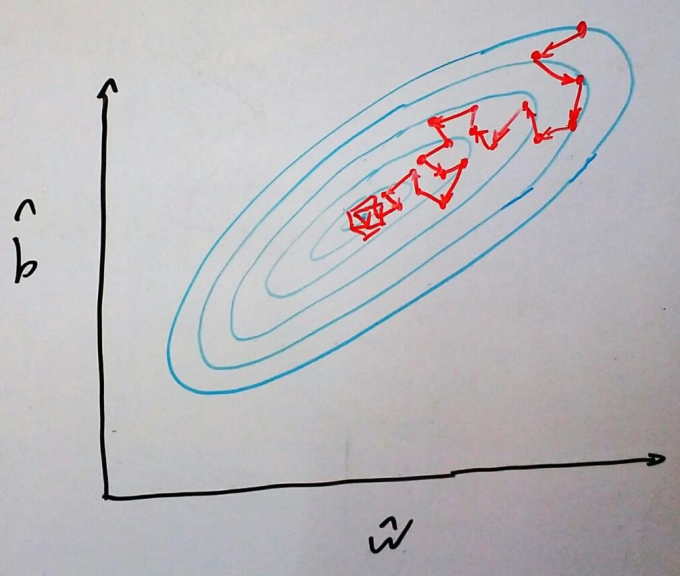
Um outro detalhe que vale a pena mencionar é que GDE normalmente não converge, mas fica vagando em alguma região próxima ao ponto de mínimo. Na prática, isso não é um problema, pois nessa região o custo já é baixo o suficiente. De qualquer forma, é uma boa visualizar um exemplo do tipo de trajeto que GDE percorrerá numa superfície de custo:
E finalmente, nossa implementação de GDE:
np.random.seed(23)
# implementa regressão linear com gradiente descendente estocástico
class linear_regr(object):
def __init__(self, learning_rate=0.0001, batch_size=5, training_iters=50):
self.learning_rate = learning_rate
self.training_iters = training_iters
self.batch_size = batch_size
def fit(self, X_train, y_train, plot=False):
# formata os dados
if len(X_train.values.shape) < 2:
X = X_train.values.reshape(-1,1)
X = np.insert(X, 0, 1, 1)
# inicia os parâmetros com pequenos valores aleatórios
# (nosso chute razoável)
self.w_hat = np.random.normal(0,5, size = X[0].shape)
for i in range(self.training_iters):
# cria os mini-lotes
offset = (i * self.batch_size) % (y_train.shape[0] - self.batch_size)
batch_X = X[offset:(offset + self.batch_size), :]
batch_y = y_train[offset:(offset + self.batch_size)]
gradient = np.zeros(self.w_hat.shape) # inicia o gradiente
# atualiza o gradiente com informação dos pontos do lote
for point, yi in zip(batch_X, batch_y):
gradient += (point * self.w_hat - yi) * point
gradient *= self.learning_rate
self.w_hat -= gradient
def predict(self, X_test):
# formata os dados
if len(X_test.values.shape) < 2:
X = X_test.values.reshape(-1,1)
X = np.insert(X, 0, 1, 1)
return np.dot(X, self.w_hat)
regr = linear_regr(learning_rate=0.0003, training_iters=40)
regr.fit(dados['x'], dados['y'])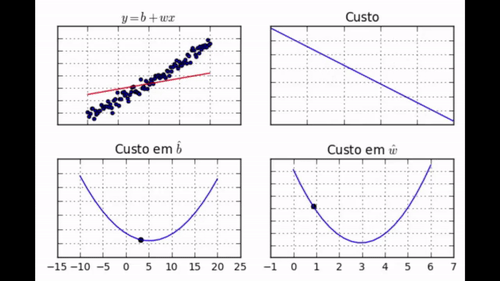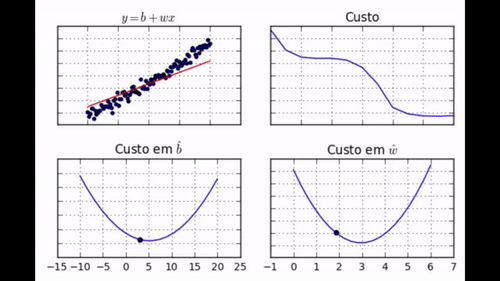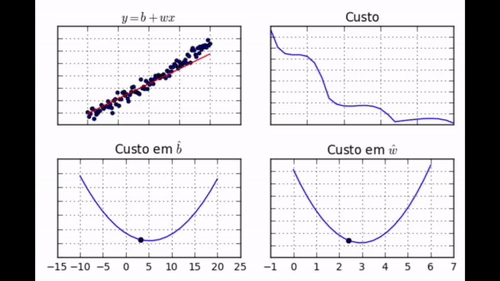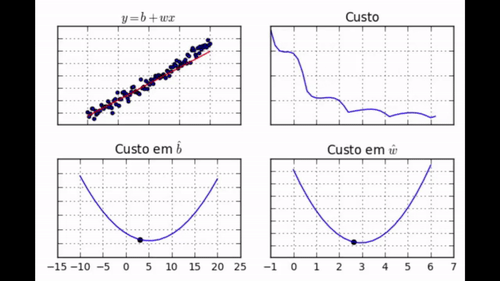
Note como nem todos os passos nos levam em direção ao mínimo. Além disso, perceba como, no final do aprendizado, jamais chegamos ao mínimo, mas ficamos vagando em torno dele.</div>
Explorando melhorias: acelerando GDE
GDE por si só já é um método bastante popular para treinar modelos de Aprendizado de Máquina. Mesmo assim, várias extensões e variações foram propostas com o intuito de diminuir as flutuações na função custo ou acelerar o processo de treinamento. Aqui, vamos explorar apenas uma delas, mas saiba que muitas outras existem.
Como já dissemos, a diferença fundamental entre o método de gradiente descendente e o processo de uma bolinha de gude descendo em uma cuia é que a bolinha acumula momento, acelerando conforme desce. Em outras palavras, quando a direção de descida é a mesma, a bolinha aumenta a velocidade. Isso é definitivamente uma propriedade que gostaríamos de ter no nosso processo de aprendizado por GDE: se estamos indo na direção certa, é uma boa ideia acelerar!
Não se preocupe, é fácil modificar GDE para incorporar momento. Para isso, basta sabermos a velocidade passada da bolinha e atualizá-la conforme o processo de descida. Além disso, nós agora vamos atualizar os parâmetros conforme a velocidade, em vez de utilizar apenas o gradiente. Eis a nova regra de atualização dos parâmetros:
\[\pmb{v_t} := \gamma \pmb{v_{t-1}} + \alpha \nabla(L))\] \[\pmb{\hat{w}} := \pmb{\hat{w}} - \pmb{v_t}\]Na primeira linha, nós atualizamos a velocidade. O termo \( \gamma v_{t-1} \) funciona como um atrito ou resistência do ar, diminuindo a velocidade em uma porcentagem \( 1-\gamma \) da velocidade anterior. Pense nele como alguma viscosidade que nos impede de acelerar. \( \gamma \) é mais um hiper-parâmetro que precisa ser ajustado manualmente. O termo seguinte, \( \alpha \nabla(L)) \), incorpora a informação da inclinação da descida.
E por fim, nossa implementação.
np.random.seed(23)
# implementa regressão linear
# com gradiente descendente estocástico e momento
class linear_regr(object):
def __init__(self, learning_rate=0.0001, batch_size=5, gamma=0.9, training_iters=50):
self.learning_rate = learning_rate
self.training_iters = training_iters
self.batch_size = batch_size
self.gamma = gamma
def fit(self, X_train, y_train, plot=False):
# formata os dados
if len(X_train.values.shape) < 2:
X = X_train.values.reshape(-1,1)
X = np.insert(X, 0, 1, 1)
# inicia os parâmetros com pequenos valores aleatórios
# (nosso chute razoável)
self.w_hat = np.random.normal(0,5, size = X[0].shape)
velocidade = np.zeros(self.w_hat.shape) # inicia a velocidade
for i in range(self.training_iters):
# cria os mini-lotes
offset = (i * self.batch_size) % (y_train.shape[0] - self.batch_size)
batch_X = X[offset:(offset + self.batch_size), :]
batch_y = y_train[offset:(offset + self.batch_size)]
gradient = np.zeros(self.w_hat.shape) # inicia o gradiente
# atualiza o gradiente com informação dos pontos do lote
for point, yi in zip(batch_X, batch_y):
gradient += (point * self.w_hat - yi) * point
gradient *= self.learning_rate
# atualiza a velocidade
velocidade = (velocidade * self.gamma) + gradient
self.w_hat -= velocidade # atualiza a os parâmetros
def predict(self, X_test):
# formata os dados
if len(X_test.values.shape) < 2:
X = X_test.values.reshape(-1,1)
X = np.insert(X, 0, 1, 1)
return np.dot(X, self.w_hat)
regr = linear_regr(learning_rate=0.0001, training_iters=30)
regr.fit(dados['x'], dados['y'])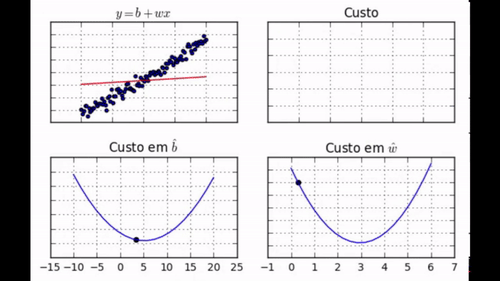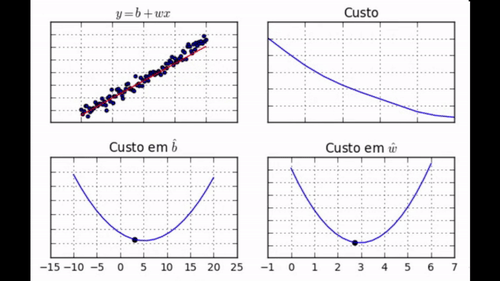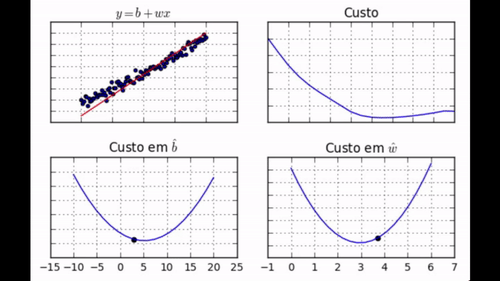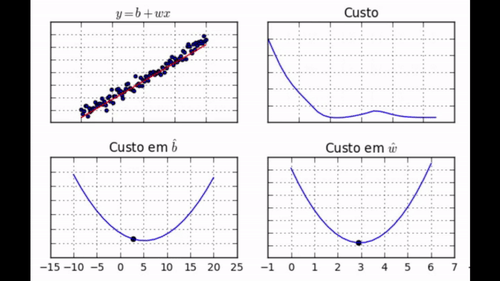
Usando gradiente descendente na prática
Se você prestou atenção até aqui, sabe que para implementar gradiente descendente precisamos das derivadas parciais da função custo com relação aos parâmetros que queremos otimizar. No nosso exemplo de regressão linear simples, isso foi bem fácil de calcular, mas nem sempre isso será o caso. Felizmente para nós, na prática, as bibliotecas de programação especializadas em otimização já calculam essas derivadas automaticamente para nós. Mais ainda, nelas, gradiente descendente e suas variações já vem implementados!
Para mostrar como utilizar gradiente descendente na prática vamos utilizar uma biblioteca de aprendizado de máquina desenvolvida pelo Google e agora aberta ao público: TensorFlow. Veja como em poucas linhas podemos implementar a técnica de gradiente descendente para resolver nosso exemplo de regressão linear. Note também como podemos rodar muito mais iterações mais rapidamente:
import tensorflow as tf
import numpy as np
x, y = dados['x'].values, dados['y'].values # dados
# Monta a estrutura tf
# valores iniciais shape
W_hat = tf.Variable(tf.random_normal([1], 0, 5))
b_hat = tf.Variable(tf.zeros([1]))
# modelo
y_hat = W_hat * x + b_hat
# Função custo
loss = tf.reduce_mean(tf.square(y_hat - y))
# otimizador
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)
sess = tf.Session() # para rodar a estrutura
sess.run(tf.global_variables_initializer()) # inicia variáveis
# roda 200 iterações de treino
for step in range(200):
sess.run(optimizer)
w_final, b_final = sess.run([W_hat, b_hat])
print('Após treinamento, w_hat = %.2f e w_hat = %.2f' % (w_final[0], b_final[0]))
sess.close() Após treinamento, w_hat = 2.96 e w_hat = 5.09
Uma grande vantagem dessas bibliotecas é que elas são otimizadas para realizar operações algébricas muito rapidamente. Nós vimos que GDE pode ser definido em termos de varias operações com vetores e matrizes e esse tipo de operação pode ser paralelizado facilmente. Assim, se você tem um computador com uma placa de vídeo (GPU) a otimização por GDE será extremamente rápida.
Ligações externas
Dada a sua importância, há muitas fontes excelentes para aprender sobre gradiente descendente:
- Os vídeos do curso online de Neural Networks for Machine Learning, da universidade de Toronto, são provavelmente a melhor fonte para estudar gradiente descendente. Todos os vídeos desta seção do curso são excelentes para aprender bastante sobre gradiente descendente e suas extensões.
- Os vídeos 1, 2 e 3 sobre gradiente descendente com regressão linear de uma variável (do curso de Machine Learning com o professor Ng) cobrem a maioria do conteúdo que vimos aqui com bastante visualização e de maneira intuitiva. Além disso, o vídeo 4 do mesmo curso mostra bem a intuição de GDE
- Os vídeos 1 e 2 do custo de Deep Learning do Google resumem bem GDE, dão dicas de como acelerar o aprendizado e ainda falam sobre a extensão do algoritmo com momento - embora um pouco diferente da nossa.











