AM Essencial

Posted on 6/06/2017

Conteúdo

O que é Aprendizado de Máquina?
1. AM ou Estatística?
2. Onde se usa AM?
Introdução ao Aprendizado de Máquina
Aprendendo AM por conta própria
1. Uma conversa motivacional com meus colegas de humanas

1 - O que é Aprendizado de Máquina?

A maioria dos livros e artigos que conheço apresentam Aprendizado de Máquina (A.M.) como um sub-campo de inteligência artificial; mais do que isso, de acordo com Goodfellow et al, "Aprendizado de Máquina é o único meio viável pelo qual é possível construir sistemas que consigam operar em complicados ambientes reais". De minha parte, reconheço AM como um campo da estatística e computação, que começou dentro da área de IA, mas hoje se estende muito além dela.

Em termos gerais, AM é a ciência de fazer com que os computadores aprendam a realizar alguma tarefa sem serem explicitamente programados para isso. Em termos mais técnicos, segundo Mitchell, AM é quando um computador, por meio de uma experiência E, melhora sua habilidade em uma tarefa T, de acordo com alguma métrica de performance P. Assim, AM é útil em cenários em que não sabemos como escrever um programa para resolver um problema e delegamos isso a máquina.

1.1 - AM ou Estatística?

Tanto Aprendizado de Máquina quanto Estatística se dedicam, em boa parte, a resolver problemas em cenários de incerteza, isto é, quando não é possível fazer afirmações sem alguma margem de erro. Além disso, ambas compartilham uma grande base teórica - o princípio de maximização da verossimilhança - e até têm as mesmas ferramentas - como regressão linear e logística. Assim, uma dúvida natural que surge é: qual a diferença entre Estatística e Aprendizado de Máquina? Infelizmente, a linha que as separa é muito tênue; cada vez mais essas duas ciências estão convergindo, de forma que não é possível responder essa questão de forma geral. Mesmo assim, podemos perceber algumas diferenças quanto aos objetivos de cada uma delas.

Em Estatística, há uma grande preocupação em utilizar dados para estabelecer conclusões estatisticamente válidas entre as variáveis, utilizando modelos probabilísticos. Por exemplo, nós podemos construir um modelo para estimar se a presença de computadores em sala de aula melhora o desempenho dos alunos no ENEM, de forma estatisticamente significante e mantida as demais variáveis constantes. Para tanto, é preciso ser extremamente rigoroso com a forma de coleta dos dados, com as hipóteses assumidas pelo modelo e com as interpretações dos resultados. Aprendizado de Máquina, por outro lado, está mais preocupado em realizar previsões acuradas e consistentes, como por exemplo prever a nota de um aluno no ENEM, dadas as variáveis da escola onde ele estudou. Assim, o rigor das inferências probabilísticas e a interpretação dos modelos é posta em segundo plano. Note que essa distinção nem sempre é válida, como por exemplo nos cenários em que não há previsão a ser feita e o interesse principal é achar estrutura nos dados.

1.2 - Onde se usa AM?

Divido em dois os tipos gerais de tarefa em que a utilização de Aprendizado de Máquina é recomendada:

Quando queremos resolver um problema no qual nós humanos somos muito ruins, ou mesmo quando esse problema está além da nossa capacidade cognitiva. Esses tipos de problemas normalmente envolvem muitas variáveis, em um nível que nós humanos não conseguimos processar ao mesmo tempo. Alguns exemplos desses problemas são dirigir, realizar um planejamento financeiro, prever se um relacionamento tem futuro, contratar pessoas, detectar transferências bancárias fraudulentas, estimar a demanda futura de um produto, organizar a economia ou a política de um país, proteger o meio ambiente, atenuar a pobreza, desenhar estratégias de futebol, aplicar na bolsa de valores, etc.

Quando temos um problema que sabemos resolver como humanos, mas não sabemos em detalhes como somos capazes de fazê-lo. Esse segundo tipo de problema geralmente é o característico de IA, como, por exemplo, enxergar, ouvir, ler e resumir um texto, traduzir um artigo, conversar e responder perguntas, desenhar um quadro, recomendar um filme, classificar espécies ou obras de arte, etc.

Para mais detalhes sobre quando utilizar AM, sugiro esta aula da universidade de Oxford.

Atualmente, embora AM ainda não tenha resolvido muito dos problemas que citei, as ferramentas desse campo já são postas em prática com bastante sucesso em diversas aplicações, de forma que praticamente todos que têm acesso à internet convivem com algoritmos de AM diariamente: eles são utilizados para organizar o feed de notícias do seu Facebook, ranquear resultados de pesquisa em ferramentas de busca on-line, sugerir filmes (Netflix) ou livros (Amazon), auto-completar palavras no seu celular, organizar sua agenda (Google Now), traduzir textos (Google tradutor), identificar faces nas suas fotos ou reconhecer a sua voz. Além desses exemplos mais perceptíveis, AM também melhora nossas vidas de forma que muitas vezes nem notamos. Por exemplo, AM está presente quando o banco detecta alguma atividade irregular com o seu cartão de crédito ou quando você realiza algum exame médico para diagnósticos.

Como a solução desses problemas já está bem estabelecida no mercado, é provável que nós não mais as vemos como inteligência, e sim meramente como indústria. Mas saiba que os princípios de AM utilizado nas aplicações citadas acima são os mesmos presentes em aplicações mais exóticas de IA, essas sim verdadeiramente impressionantes - provavelmente apenas porque menos cotidianas.

Apenas para citar alguns desses exemplos, em fevereiro de 2017 acadêmicos do Google publicaram um artigo em que criavam imagens de alta resolução a partir de apenas alguns pixels! Em 2016, alguns pesquisadores do MIT desenvolveram uma máquina capaz de aprender o que mais nos assusta. Além disso, existem carros que dirigem sozinhos, redes neurais artificiais capazes de imitar a escrita humana, experimentos artísticos, máquinas capazes de imaginar e vários outros experimentos que você pode inclusive ajudar participando.

2 - Introdução ao Aprendizado de Máquina

Aprendizado de Máquina pode ser visto como um problema estatístico e de otimização. Nós normalmente estamos interessados em mapear um fenômeno por meio de uma função. Essa função é o que chamamos de modelo: uma fórmula que representa da melhor forma possível como funciona o fenômeno que nos interessa. Mas o que é essa "melhor forma possível"? Em primeiro lugar, nós gostaríamos que a semelhança entre o fenômeno observado e o nosso modelo fosse maximizada. Mas mais do que isso, entre dois modelos que descrevem igualmente bem o fenômeno, nós preferimos aquele que for mais simples. Esse segundo critério é um princípio que chamamos Navalha de Occam.

Para entender um fenômeno, nós precisamos coletar dados sobre ele. Quase nunca é possível fazer isso de forma perfeita. Pense, por exemplo, no fenômeno de felicidade matrimonial. Não é possível medir felicidade diretamente, então temos que inventar formas criativas, mas imperfeitas, de medi-la indiretamente, talvez por algum experimento ou questionário. Por conta dessa imperfeição na coleta, os dados estão sempre corrompidos por ruídos aleatórios. Por isso dizemos que AM é em grande parte um problema estatístico, pois tem de fazer estimativas e aproximações sujeitas a erro. Nosso objetivo será sempre minimizar esse erro.

2.1 - Os três tipos de aprendizado

É comum distinguirem 3 tipos ou regimes de Aprendizado de Máquina: supervisionado, não supervisionado e por reforço. Mas é bom saber que a fronteira entre eles está longe de ser clara e muitas vezes os tipos de aprendizado se misturam em um mesmo problema.

2.1.1 - Aprendizado supervisionado

Aprendizado supervisionado é quando queremos prever uma variável \( y \) que depende de outras variáveis \( X \). Nesse cenário, nós mostramos à máquina as variáveis \( X \) e \( y \). Então pedimos que ela reproduza \( y \) a partir de \( X \). A nossa esperança é que, após ser apresentada a vários exemplos de pares (\( X \), \( y \)), a máquina consiga prever bem \( y \) de observações que nunca viu, dada as variáveis \( X \) desses observações. Isso é chamado de aprendizado supervisionado pois podemos traçar uma analogia com a noção de um aprendiz - o computador - sendo supervisionado por um professor - nós - que lhe fornece vários exemplos de como realizar corretamente uma tarefa.

Matematicamente, nos queremos mover de uma estimativa incondicional de \( y \), geralmente a esperança \( E[y] \), para uma estimativa condicional de \( y \), geralmente a esperança de \( y \) dado \( X \), \( E[y|X] \). Nós fazemos isso usando algum modelo para estimar \( f(X) = y + \epsilon \), em que \( \epsilon \) é um ruído aleatório. Quase sempre esse problema é posto explicitamente como um problema de otimização, no qual minimizamos um erro que mede a diferença entre a nossa estimativa de \( f(X) \) (normalmente chamada de \( \hat{y} \) ) e \( y \).

Podemos identificar dois tipos de problemas dentro do regime de aprendizado supervisionado: regressão e classificação. Problemas de regressão são aqueles em que queremos prever um valor contínuo, como renda, peso, quantidade demandada, ângulo da direção de um carro automático ou quando acontecerá a promoção de um produto. Problemas de classificação são aqueles em que queremos prever um valor discreto, ou seja classificar um exemplo segundo uma categoria. Alguns exemplos são identificar a presença de uma doença dado os sintomas do paciente, prever se o preço da ação de uma empresa vai subir ou cair dado o histórico do mercado financeiro, identificar de que pessoa é a face em uma imagem ou classificar um livro em uma escola literária.

A maioria dos trabalhos em AM são feitas sob o regime de aprendizado supervisionado, talvez porque sejam bem definidos e apresentem bastante utilidade prática. Alguns dos algoritmos que podem ser usados para resolver esse tipo de problema são regressão linear, regressão logística, árvores de decisão, florestas aleatórias, máquinas de suporte vetorial, k-vizinhos mais próximos, Bayes ingênuo e redes neurais artificiais. Resumindo, qualquer problema em que se busca prever uma variável \( y \) a partir de variáveis \( X \) tem o potencial para ser resolvido com aprendizado de máquina supervisionado.

2.1.1.1 - Aprendizado semi-supervisionado

Entre aprendizado supervisionado e não supervisionado, existem ainda as técnicas de aprendizado semi-supervisionado. Para obter bons resultados com AM supervisionado, normalmente é preciso de muitas observações de variáveis de entrada \( X \), etiquetadas com as variáveis de saída \( y \). No entanto, dados nomeados com \( y \) são escassos, muitas vezes porque o custo de nomeá-los é alto demais. Pense por exemplo, em um estudo que tenta mapear o aparecimento de algum desconforto após uma vacinação experimental, dada as características físicas de uma pessoa. Nesse caso, seria custoso demais vacinar experimentalmente milhares de pessoas; por outro lado, coletar as características físicas delas é bem mais simples.

Aprendizado de Máquina semi-supervisionado atua nesses cenários, em que muitas das observações \( X \) não estão nomeadas com seus pares \( y \). Essa é ainda uma das fronteiras do conhecimento de AM, onde as aplicações bem sucedidas não são tão abundantes. Talvez os avanços mais notáveis obtidos com aprendizado semi-supervisionado são na área de processamento de linguagem natural, quando primeiro se aprende regras semânticas para as palavras e depois utiliza-se a semântica aprendida para realizar previsões

2.1.2 - Aprendizado não supervisionado

Aprendizado não supervisionado é quando temos apenas dados \( X \), sem os pares \( y \). Nesse tipo de regime, estamos tentando achar alguma estrutura nos dados, o que pode muitas vezes ser traduzido em um problema de achar uma representação mais simples de \( X \), \( \hat{X} \). Problemas de aprendizado não supervisionado não são tão bem definidos como os supervisionados, mas eles ainda podem ser vistos como um problema estatístico e de otimização. Como já argumentamos, os dados \( X \) quase sempre vem corrompidos com ruído. Nós podemos então postular um problema não supervisionado em que o objetivo seja achar uma representação de \( X \), \( \hat{X} \), mas que seja livre de ruído. Outra possibilidade é achar uma representação simplificada de \( X \), onde essa forma simplificada retenha apenas as características mais importantes de \( X \). AM não supervisionado pode ser visto como um problema de otimização pois muitas vezes é realizado de forma que o objetivo seja simplificar \( X \) em \( \hat{X} \), mas de forma que a diferença entre \( X \) e \( \hat{X} \) seja minimizada.

AM não supervisionado pode ser usado em conjunto com AM supervisionado, sendo que o primeiro é como uma etapa de processamento dos dados para o segundo. Algumas aplicações de AM não supervisionado são segmentação de consumidores (algoritmos de clusters), visualização de dados multidimensionais, compressão de dados e análise de mídias sociais. Alguns dos algoritmos que podem ser usados para resolver esse tipo de problema são análise de componentes principais, análise de componentes independentes, clusters "k-means", Esperança-Maximização, Autocodificadores e t-SNE.

2.1.3 - Aprendizado por reforço

Aprendizado por reforço é quando, em um certo ambiente, queremos mapear que ações tomar, dado o estado do ambiente. Nesse caso, nosso objetivo deixa de ser estimar uma função que mapeia \( X \) em \( y \) e passa a ser aprender uma política que mapeia \( S \) (estados) em \( A \) (ações). Cada par (\( S \), \( A \)) está associado a uma recompensa, de forma que o computador aprende a melhor política ao maximizar a recompensa ao longo das interações com o ambiente.

AM por reforço tem bastante influência da Psicologia e da Economia, particularmente do campo de teoria dos jogos. Algumas das aplicações de AM por reforço são construir oponentes em videogames, movimentação de robôs, simulações de ambientes complexos e aprender estratégias de troca no mercado financeiro.

2.2 - Capacidade e generalização

Capacidade e generalização são as duas qualidades que gostaríamos que nossos modelos de AM adquirissem: a primeira lhe da força para aprender as regularidades nos dados em que treinamos o modelo; a segunda faz com que ele consiga generalizar o que aprendeu para dados novos. Infelizmente essas duas forças então em polos opostos, de forma que ter mais de uma geralmente significa perder mais da outra. A seguir, vamos detalhar bem como esse tradeoff acontece e como ponderar essas duas forças.

Considere um problema de regressão, no qual temos dados sobre as variáveis independentes, \( X \), e as variáveis dependentes \( y \). Nós então gostaríamos de prever \( y \) a partir de \( X \). Vamos usar como exemplo um problema simples, com apenas uma variável dependente, \( x \). Digamos que nos interessa saber como os gastos em capital de uma determinada empresa (\( x \)), se refletem no lucro dessa empresa (\( y \)). Agora suponha que o fenômeno que converte capital (\( x \)) em lucro (\( y \)) seja descrito pela equação \( y = sen(2x) + 1.5x + 2 \). A parte \( 1.5x \) da função indica como o lucro aumenta com os gastos em capital; já a parte \( sen(2x) \) adiciona um componente de intervalos: são os custos que empresa tem quando precisa mudar para um espaço maior, algo que acontece em algumas etapas do crescimento. 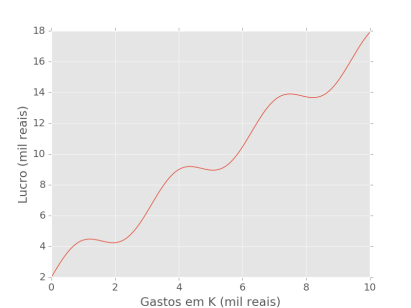sin_lucro_true

No entanto, como pessoas ignorantes que somos, não temos acesso a essa informação. Nós então coletamos 15 observações de lucro e gastos de capital da empresa e recorremos às ferramentas de Aprendizado de Máquina na esperança de descobrir como essas variáveis se relacionam. Como sempre, essas observações vem corrompidas com algum ruído aleatório que mascara a relação que queremos descobrir:

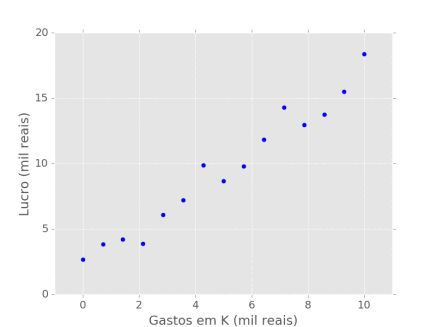
data_curr

2.2.1 - Teorema "Não há almoço grátis"

O problema que temos é complexo: temos que aprender uma regra geral para a relação entre \( x \) e \( y \), mas utilizando apenas alguns exemplos. Como aponta Goodfellow et al (2016), isso é contraditório. Do ponto de vista lógico, não podemos inferir regras gerais a partir de uma quantidade limitada de exemplo. Nós então focamos em um problema mais simples: aprender uma regra que está aproximadamente correta na maioria dos casos. É importante lembrar que tudo o que estimamos, estimamos com erro!

Devemos então escolher algum algoritmo para aprender essa regra provavelmente aproximadamente correta (PAC). No entanto, o teorema "Não há almoço grátis" (Wolpert, 1996) nos diz que nenhum algoritmo de Aprendizado de Máquina é melhor do que outro universalmente. Felizmente, só precisamos de um algoritmo que seja melhor no nosso problema particular, e isso é possível de encontrar.

2.2.2 - Sobre e sub ajustamento

Independentemente do algoritmo que escolhermos para resolver nosso problema, sempre poderemos ajustá-lo para ter mais ou menos capacidade. Nós então escolhemos algum algoritmo de Aprendizado de Máquina e aprendemos 3 modelos a partir dos dados coletados, cada um com uma capacidade diferente:

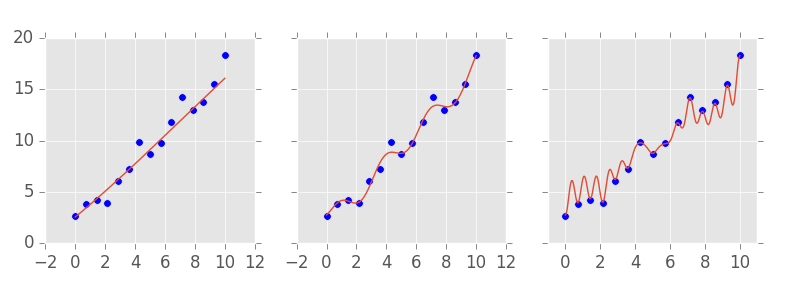
models

O nosso primeiro modelo tinha uma capacidade muito baixa, errando muitos pontos por uma boa distância. Nós então aumentamos a capacidade do modelo, e no segundo a linha prevista já passa mais próxima aos dados. Na nossa terceira tentativa, aumentamos mais ainda a capacidade e finalmente conseguimos um modelo passa por todos os pontos. Nós então apresentamos os três modelos para o dono da empresa, como uma forma de ele saber quanto vai lucrar dado o tanto que investir. Mas a pergunta que permanece é um dos grades desafios de Aprendizado de Máquina: qual dos modelos é melhor?

No momento, não temos os meios suficientes para responder essa pergunta. O que podemos saber é qual a performance de cada modelo nos dados que a máquina observou durante o treinamento. Esses dados são chamados de set de treino. No entanto, o que gostaríamos dos nossos modelos é que eles fossem capazes de prever \( y \) a partir de novas observações de \( x \), que não foram vistas no treinamento. Em outras palavras, queremos que nossas previsões generalizam para observações ainda não vistas.

O dono da empresa então decide esperar mais um pouco antes de seguir as recomendações de investimento dos nossos modelos. Com o tempo, conseguimos coletar mais dados sobre o capital e o lucro da nossa empresa de interesse e vemos como os modelos se sairiam se tentassem prever os lucros observados a partir dos gastos com capital:

test

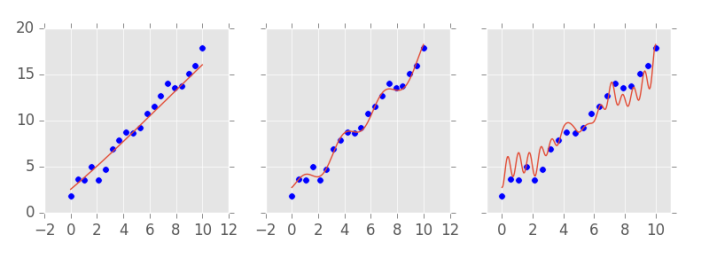
Essas novas observações, que não foram utilizadas para treinar o modelo, são chamadas de set de teste. Com elas, é possível descobrir o erro de generalização do nosso modelo e definir qual deles é o melhor. Agora está claro que o modelo do meio, com capacidade média, é o melhor. Para ser mais específico, o modelo do meio é capaz de explicar 99% da variação no lucro (de acordo com a medida \( R^2 \)), ao passo que o primeiro modelo explica 96% e o último, apenas 92%.

Em Aprendizado de Máquina, dizemos que o primeiro modelo esta sofrendo de sub-ajustamento, isto é, ele tem uma capacidade tão baixa que não consegue aprender as regularidades presentes nem no set de treinamento. Nesse cenário, a performance nos sets de treino e de teste costumam ser baixas. O terceiro modelo, por sua vez, sofre de sobre-ajustamento, isto é, tem uma capacidade tão alta que além de aprender as regularidades, aprendeu também o ruído presente nos dados de treino. Nesse cenário, o erro no set de treino é extremamente baixo, mas o erro de generalização - erro no set de teste - é alto. O modelo do centro parece ter aprendido bem as regularidades dos dados sem aprender os ruídos no set de treino. Nesse cenário, os erros no set de treino e teste são parecidos e satisfatórios.

2.2.3 Viés e variância

Na absoluta maioria dos casos, a previsão de um modelo de Aprendizado de Máquina é a média de uma distribuição condicional, \( E[y|X] \) ou \( E[y|X, \hat{w}] \). Por exemplo, no segundo modelo apresentado acima, quando o gasto com capital é 6 mil, é previsto que o lucro será, na média, de 10 mil. Podemos dizer que o nosso modelo aprendeu os parâmetros \( \hat{w} \) que descrevem a curva vermelha. Mas essa curva vermelha é apenas uma estimação da verdadeira função geradora dos dados. O máximo que podemos esperar é que a curva estimada e a verdadeira sejam o mais similares possível. Em outras palavras, queremos que os parâmetros \( \hat{w} \) que descrevem a curva estimada sejam o mais próximo possível dos parâmetros \( w \) da curva verdadeira.

Nós podemos tratar \( \hat{w} \) como uma variável aleatória. Pense nela como vários parâmetros que seriam aprendidos se utilizássemos apenas uma sub-amostra dos nossos dados para treinar vários modelos. Podemos então definir viés como a diferença entre a esperança dessa variável aleatória e os verdadeiros parâmetros do processo gerador dos dados: \( E[\hat{w}] -w \). Quando essa diferença é zero, temos um estimador \( \hat{w} \) que é não enviesado, algo que realmente gostaríamos que nossos modelos aprendessem. É importante lembrar que o viés mede a diferença esperada entre a função estimada e o verdadeiro processo gerador de dados.

Além do viés, também precisamos considerar como as nossas estimativas variam com diferentes amostras. Isso pode ser medido pela variância: \( Var(\hat{w}) \). Nós gostaríamos que a variância também fosse baixa, pois não queremos que o tipo de previsão do nosso modelo dependa bruscamente da amostra de dados em que ele foi treinado. Quando um modelo tem muita variância, a qualidade das nossas previsões dependerá muito da amostra que escolhermos para prever.

Matematicamente, podemos mostrar que viés e variância são duas fontes de erro. Mais especificamente, a média do erro quadrado pode ser decomposta em viés e variância:

\( \pmb{MSE= Vies(\hat{w})^2 + Var(\hat{w})} \).

Voltemos aos três modelos acima. O primeiro deles foi estimado com pouca variância. Como o algoritmo utilizado no aprendizado tinha pouca capacidade, os modelos que podem ser aprendidos são enviesados para aprender uma reta, não variando muito com os dados utilizados no treinamento, já que é incapaz de aprender as pequenas curvaturas. Isso é um fenômeno mais geral: algoritmos com pouca capacidade aprendem modelos que sofrem de sub-ajustamento e são enviesados, mas com pouca variância. O inverso também acontece: o nosso terceiro modelo não tem quase viés algum, mas sofre de muita variância (imagem traduzida de Goodfellow et al):

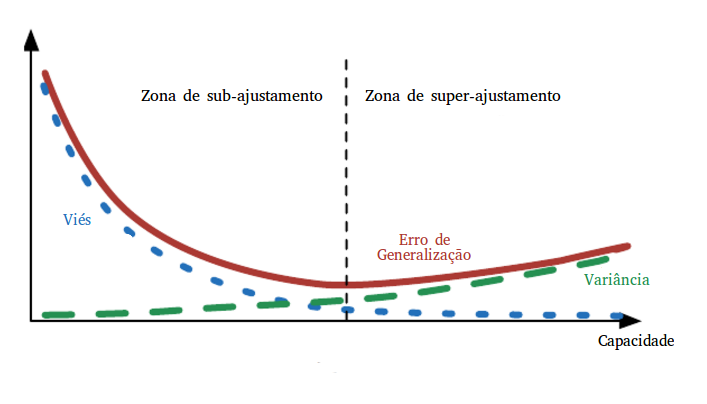
Um detalhe muito importante é que a variância pode ser diminuída aumentando a quantidade de dados de treinamento, algo que não pode ser feito com o viés. Pense no algoritmo utilizado para gerar o terceiro modelo, por exemplo. Se utilizássemos muitos dados de treinamento, eventualmente a sua capacidade não seria mais suficiente para passar por todos os pontos, ele então deixaria de aprender ruído para se concentrar em aprender o sinal do processo gerador de dados. Em se tratando do primeiro modelo, não importa quantos dados utilizássemos para treinar, ele não aprenderia o sinal correto pois não tem capacidade para isso. No geral, erro de variação e erro de treinamento convergem quando o tamanho da amostra de treinamento cresce:

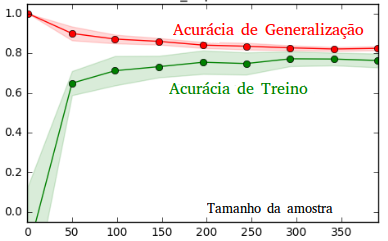
learning curve

Como não conseguimos aumentar a quantidade de dados infinitamente, a grande questão de Aprendizado de Máquina é como ajustar a capacidade de forma a balancear variância e viés, de forma que nem sobre-ajustamos nem sub-ajustamos o modelo?

2.2.4 - Validação cruzada

Com o que vimos acima, sabemos que não podemos confiar em métricas de erro computadas nos sets de treinamento para escolher entre modelos, pois podemos sempre reduzir esse erro a zero simplesmente aumentando a capacidade do algoritmo de aprendizado. Há um método extremamente simples para selecionar o modelo com menor erro de generalização - o que realmente nos interessa. Após coletar os dados, nós vamos separá-los em duas sub-amostras. Uma delas, a sub-amostra de treino, será utilizada para aprender um modelo; a outra sub-amostra será utilizada para medir a performance do modelo, que será uma estimativa do erro de generalização. Para escolher a capacidade do modelo, nós dividiremos a amostra de treino mais uma vez: em um novo set de treino e em um set que chamaremos de validação. Nós então treinaremos o modelo no set de treino, ajustaremos a capacidade do algoritmo de aprendizado com base na performance no set de validação, e reportaremos uma estimativa final do erro de generalização conforme a performance no set de teste. É importante que o set de teste seja observado apenas uma única vez, na hora de reportar a estimativa de erro final. Se múltiplas tentativas forem feitas e comparadas com base no erro no set de teste, esta medida de erro não será confiável como uma estimativa do erro de generalização e o modelo provavelmente performará pior do que o esperado, quando utilizado na prática.

Essa técnica de escolha de modelos leva o nome de validação cruzada. Ela pode parecer óbvia e simples, mas atualmente é completamente ignorada pela maioria dos trabalhos em Economia que conheço. A econometrista, Susan Athey, que atua na área de Aprendizado de Máquina em Economia e foi premiada com a medalha John Bates Clark pelo seu trabalho, chegou a afirmar que validação cruzada é talvez a maior contribuição que a ciência de AM pôde fazer às Ciências Sociais. Pode-se argumentar que, como a maioria dos trabalho de economia lida com modelos de pouca capacidade, validação cruzada não seria necessário, já que eles estariam em um regime de sub-ajustamento, no qual erro de treino e de generalização são similares. Eu particularmente acho um pouco perturbador o fato de que muitos trabalhos estejam sendo publicados tendo o erro de treinamento como medida final de erro; da minha experiência, percebi que mesmo os modelos lineares simples usados em economia já têm capacidade suficiente para que os erros de treino sejam muito menores do que erros no set de teste.

Além disso, podemos perceber como é fácil trapacear ao reportar uma medida de erro de teste: basta dizer que utilizou apenas o set de validação para ajustar a capacidade quando na verdade utilizou-se o set de teste. Por conta disso, é importante que todo o trabalho feito com Aprendizado de Máquina seja reprodutível, de forma que outras pessoas possam testar o modelo em dados não vistos pelo pesquisador e assim garantir a qualidade do trabalho. Não fazer isso pode causar danos, muitas vezes gravíssimos.

2.3 Ligações Externas

Aqui, só posso fazer uma brevíssima introdução ao Aprendizado de Máquina, até porque não sou especialista no assunto. Para mais detalhes e informações mais confiáveis eu sugiro:

A introdução do livro de Ethem Alpaydin, Introduction to Machine Learning (2nd ed., 2014).
O capítulo 5 do excelente livro de Goodfellow et al, Deep Learning (2016).
A introdução do curso da Universidade de Stanford sobre Aprendizado de Máquina no Coursera, lecionado pelo professor Ng.
Essa primeira aula incrível, gravada no curso de Aprendizado de Máquina da universidade de Oxford (2014-2015), lecionado pelo professor Nando de Freitas.

3 - Aprendendo AM por conta própria.

Se você considera aprender AM saiba que não será um caminho fácil - e talvez por isso que profissionais da área são tão escassos. Antes de tudo, é preciso saber inglês, já que a maioria do conteúdo é nessa língua. Em segundo lugar, terá que cobrir alguns pré-requisitos matemáticos e computacionais. É fundamental ter um sólido conhecimento em cálculo e uma boa base em álgebra linear. Felizmente o MIT tem cursos gravados excelentes nesses assuntos (cálculo univariado, cálculo multivariado, introdução à álgebra linear), e tudo de graça. Em seguida, é preciso se familiarizar com o básico de estatística e probabilidade. Para isso, eu recomendo os cursos abertos da Udacity sobre estatística descritiva e inferencial. Depois de tudo isso, é preciso se familiarizar com o básico de ciência da computação. Há muitas formas de fazer isso e eu sugiro que pesquise qual lhe será mais adequada. Da minha parte, preferi aprender ciência da computação tendo Python como minha principal linguagem. Para isso, alguns links podem ser úteis: [1], [2], [3].

Tendo os pré-requisitos acima, resta só escolher onde aprender AM. A minha sugestão é fazer todos os cursos que vou sugerir, mesmo que o conteúdo seja redundante em alguns aspectos. A verdade é que AM é difícil o suficiente para que rever o mesmo conteúdo várias vezes se torne quase uma necessidade. Segue a lista de cursos que recomendo:

Para entender bem a teoria:
- O da universidade de Stanford, talvez o mais famoso sobre o assunto (ensinado em Octave/Matlab).
- O da universidade de Toronto, ótimo para se você optar por se aprofundar em redes neurais artificiais - a melhor ferramenta de AM na minha opinião (ensinado em Octave/Matlab).
- O da universidade de Oxford tem as melhores vídeo aulas que encontrei (ensinado em Lua)
- O da universidade Georgia Tech, o mais abrangente de todos (ensinado em Python).

Para aplicar a teoria:
- Introdução a AM, da Udacity ensina sobre a biblioteca sklearn, para aplicações simples do dia a dia (ensinado em Python).
- O curso de Deep Learning, do Google, que ensina sobre a biblioteca TensorFlow, para aqueles que querem aprender sobre AM no estado da arte (ensinado em Python).

Quando comecei a aprender AM, não sabia ao certo o que estudar e por conta disso acabei gastando meu tempo com coisas desnecessárias, mesmo que muito interessantes (por exemplo aprendendo JavaScript orientado a objetos). Assim, creio que seja importante também listar o que você não precisa aprender (provavelmente alguém pode ficar irritado com o que vêm a seguir, mas essas são as minhas recomendações, segundo o que funcionou comigo). Em primeiro lugar, saiba que é estritamente necessário apenas ter conhecimento básico em programação. Com um curso introdutório em ciência da computação, você já pode pular direto à parte de Aprendizado de Máquina. Não é preciso ter conhecimento de nada relacionado a redes. Não é necessário aprender ferramentas de front-end, como HTML, CSS e JavaScript. Na verdade, você sequer precisa saber o que front-end significa. É útil saber programação orientada a objetos, embora não seja estritamente necessário. Não é necessário aprender C ou C++, mas talvez isso seja útil dependendo de onde você vai trabalhar.

3.1 - Uma conversa motivacional com meus colegas de Humanas

Acredito que para a maioria de vocês, AM pode parecer intimidador pelas grandes exigências em conhecimento matemático e de programação. Meu objetivo aqui é convencer vocês de que essa relutância é infundada. Em primeiro lugar, Aprendizado de Máquina não demanda muito conhecimento em programação. Pelo menos não se você pretende apenas utilizar as ferramentas desse campo, como é o meu caso (se o seu interesse for empurrar a barreira do conhecimento em AM adiante, então creio que as coisas sejam diferentes). A maioria dos algoritmos já está implementada para que nós praticantes apenas precisemos nos preocupar com o desing final, que pode ser feito em poucas linhas de código; com problemas mais simples, às vezes não é preciso nem dez linhas! Eu mesmo só sei o básico de programação e já consigo fazer algumas coisas bem interessantes com redes neurais convolucionais e máquinas de suporte vetorial.

A parte matemática, sim, demandará mais de vocês, principalmente se não estiverem acostumados, como foi meu caso. Até pedir transferência para Economia, eu cursava Relações Internacionais e uma das minhas maiores felicidade de calouro era não ter mais que lidar com matemática. No entanto, percebi quão interessante ela era a medida que me permitia juntar teoria com utilidade prática de forma tão direta. Então peguei algumas matérias da matemática como optativas e vi alguns cursos online do MIT para tirar o atraso. Uma das coisas que descobri nas minhas aulas é que alunos das exatas, como físicos, engenheiros e estatísticos, são tão ruins em matemática quanto nós de humanas; a diferença é que eles aceitam a dificuldade (as vezes porque não têm opção), enquanto nós de humanas preferimos fugir dela.

Se o seu curso de humanas foi como Relações Internacionais foi para mim, talvez você tenha muitas matérias teóricas e não consegue ver onde essa teoria possa ser aplicada. Então acredito que sentirá a mesma satisfação que eu ao descobrir uma campo científico como AM, em que praticamente toda teoria tem dezenas de aplicações práticas. Você também vai adorar conseguir enxergar o conhecimento moldando a realidade a sua volta e ler (e entender) sobre avanços que se desenvolvem em período de semanas e que mais parecem revoluções. Assim, o que no início parecia quase impossível de tão complicado, acaba se tornando tão agradável que até não parece mais estudo.