Posted on 15/02/2017
Updated on 19/07/2017
Updated on 19/07/2017
Conteúdo
- Pré-requisitos
- Intuição
- Justificativa matemática
- Desenhando e testando o algoritmo
- Considerações finais
Pré-requisitos
Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação.
Intuição
Vamos supor que tenhamos dados em tabela sobre duas variáveis: x e y. Se colocarmos cada par (x,y) em um gráfico, teremos uma figura como a seguinte:
O que o algoritmo de regressão linear faz é simplesmente achar a reta que melhor se encaixa entre os pontos:
Assim, podemos prever (com erro) um valor de y dado um valor de x. Por exemplo, nós não temos uma observação em que \(x=1\), mas gostaríamos de prever qual seria o valor de y caso x fosse 1. Basta então olhar na linha qual valor de y quando x assume o valor 1. Na imagem acima, y seria aproximadamente 2.5 (ponto amarelo).
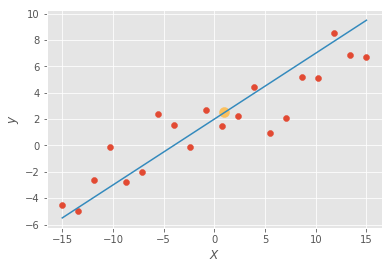
Ok. Esse exemplo é bem simples e meramente ilustrativo. Suponha agora que y não dependa mais apenas de x, mas de x e z. Bem, nesse caso, teríamos um gráfico em 3D e a regressão linear acharia o plano que melhor se encaixa nos dados. E para mais dimensões? Digamos que y dependa de 100 variáveis. Nós não podemos mais visualizar esse caso, mas sabemos que não é muito diferente dos casos 2D ou 3D, só que agora a regressão linear acha o hiperplano que melhor se encaixa nos dados. Se isso está um pouco abstrato e difícil de visualizar, pense sempre em 3D quando trabalhando com muitas dimensões. É um truque muito útil que eu aprendi em um vídeo do professor de Geoffrey Hinton e, segundo ele, todo mundo faz isso: quando tentar visualizar 100 dimensões, por exemplo, pense em 3D e grite para si mesmo "100D" e você conseguirá abstrair grandes dimensionalidades.
Justificativa matemática
Imagine que temos dados em tabela, sendo que cada linha é uma observação e cada coluna uma variável. Então escolhemos uma das colunas para ser nossa variável dependente y (aquela que queremos prever) e as outras serão as variáveis independentes (X). Nosso objetivo é aprender como chegar das variáveis independentes na variável dependente, ou, em outras palavras, prever y a partir de X. Note que X é uma matriz nxd, em que n é o número de observações e d o número de dimensões; y é um vetor coluna nx1. Podemos definir o problema como um sistema de equações em que cada equação é uma observação:
\[\begin{cases} w_0 + w_1 x_1 + ... + w_d x_1 = y_1 \\ w_0 + w_1 x_2 + ... + w_d x_2 = y_2 \\ ... \\ w_0 + w_1 x_n + ... + w_d x_n = y_n \\ \end{cases}\]Normalmente \( n > d\), isto é, temos mais observações que dimensões. Sistemas assim costumam não ter solução, pois há muitas equações e poucas variáveis para ajustar. Intuitivamente, pense que, na prática, muitas coisas afetam a variável y, principalmente se ela for algo de interesse das ciências humanas como, por exemplo, preço, desemprego, felicidade etc. Muitas das coisas que afetam y não podem ser coletadas como dados; desse modo, as equações acima não teriam solução porque não teríamos todos os fatores que afetam y.
Para lidar com esse problema, vamos adicionar nas equações um termo erro \( \varepsilon\) que representará os fatores que não conseguimos observar, erros de medição, etc.
\[\begin{cases} w_0 + w_1 x_{11} + ... + w_d x_{1d} + \varepsilon_1 = y_1 \\ w_0 + w_1 x_{21} + ... + w_d x_{2d} + \varepsilon_2 = y_2 \\ ... \\ w_0 + w_1 x_{n1} + ... + w_d x_{nd} + \varepsilon_3 = y_n \\ \end{cases}\]Ou, em forma de matriz:
\[\begin{bmatrix} 1 & x_{11} & ... & x_{1d} \\ 1 & x_{21} & ... & x_{2d} \\ \vdots & \vdots& \vdots & \vdots \\ 1 & x_{n1} & ... & x_{nd} \\ \end{bmatrix} \times \begin{bmatrix} w_0 \\ w_1 \\ \vdots \\ w_d \\ \end{bmatrix} + \begin{bmatrix} \varepsilon_0 \\ \varepsilon_1 \\ \vdots \\ \varepsilon_n \\ \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \\ \end{bmatrix}\] \[X_{nd} \pmb{w}_{d1} + \pmb{\epsilon}_{n1} = \pmb{y}_{n1}\]Para estimar a equação acima, usaremos a técnica de Mínimos Quadrados Ordinários (MQO): queremos achar os \( \pmb{\hat{w}}\) que minimizam os \( n\) \( \varepsilon^2 \), ou, na forma de vetor, \( \pmb{\epsilon}^T \pmb{\epsilon}\). Por que minimizar os erros quadrados? Assim como todo algoritmo de Aprendizado de Máquina, regressão linear também pode ser encarada como problemas de minimização de função custo. Então, nesse caso, nossa função custo é \( L = \pmb{\epsilon}^T \pmb{\epsilon}\). Um nome comum dessa função é o custo quadrático L2, pois nesse caso o custo é o quadrado da norma L2 do vetor \( \pmb{\epsilon}\). Note que nós poderíamos usar também a norma L1 do mesmo vetor como função custo. Ou ainda, poderíamos usar outras funções que adicionam uma penalidade também para o tamanho de \( \pmb{\hat{w}}\), como acontece nos algoritmos de regressão Ridge ou Lasso, mas isso terá que ficar para outro tutorial. Por hora, a soma dos mínimos quadrados bastará como função custo, até porque ela tem a vantagem de deixar a matemática muito mais simples:
\[ \pmb{\epsilon}^T \pmb{\epsilon} = (\pmb{y} - \pmb{\hat{w}}X)^T(\pmb{y} - \pmb{\hat{w}} X) \\= \pmb{y}^T \pmb{y} - \pmb{\hat{w}}^T X^T \pmb{y} - \pmb{y}^T X \pmb{\hat{w}} + \pmb{\hat{w}} X^T X \pmb{\hat{w}} \\= \pmb{y}^T \pmb{y} - 2\pmb{\hat{w}}^T X^T \pmb{y} + \pmb{\hat{w}} X^T X \pmb{\hat{w}}\]Aqui, usamos o fato de que \( \pmb{\hat{w}}^T X^T \pmb{y}\) e \( \pmb{y}^T X \pmb{\hat{w}}\) são simplesmente escalares \( 1x1\) e a transposta de um escalar é o mesmo escalar: \( \pmb{\hat{w}}^T X^T \pmb{y} = (\pmb{\hat{w}}^T X^T \pmb{y})^T = \pmb{y}^T X \pmb{\hat{w}}\). Derivando em \( \pmb{\hat{w}}\) e achando a CPO:
\[\frac{\partial \pmb{\epsilon}^T \pmb{\epsilon}}{\partial \pmb{\hat{w}}} = -2X^T\pmb{y} + 2X^T X \pmb{\hat{w}} = 0\]Derivando mais uma vez para checar a CSO chegamos em \( 2X^TX\), que é positiva definida se as colunas de\( \pmb{X}\) forem independentes. Temos então um ponto de mínimo quando:
\[\pmb{\hat{w}} = (X^T X)^{-1} X^T \pmb{y}\]Bom, parece que chegamos em algo interessante. Nos nossos dados temos \( \pmb{X}\) e \( \pmb{y}\), então podemos achar \( \hat{\pmb{w}}\) facilmente: basta substituir os valores na fórmula. O próximo passo é desenhar o algoritmo e ver como ele se sai em dados reais.
OBS:
1) A maioria dessas informações eu tirei de várias fontes na internet, mas uma que abrange tudo e mais muitas extensões são os vídeos da gravação do curso de Aprendizado de Máquina da Universidade de Oxford (2014).
2) Para mais detalhes sobre a matemática de regressão linear como MQO, veja este passo a passo da Universidade de Stanford.
3) É possível chegar em uma fórmula para os vários \( \hat{w_i}\) apenas com cálculo multivariado, sem usar álgebra linear. Para os que tem dificuldade com álgebra linear (como é o meu caso), esse método parece mais atraente. No entanto, ele tem uma notação muito mais carregada de somatórios. Da minha experiência aprendendo isso, acho que vale muito a pena investir tempo para entender bem álgebra linear, pois todos os algoritmos de Aprendizado de Máquina ficam muito mais fáceis depois. Caso queira ver como resolver a equação de otimização do algoritmo de MQO sem usar álgebra linear, eu sugiro o livro do Wooldrige.
Desenhando e testando o algoritmo
Resumindo o que vimos acima de forma intuitiva, podemos dizer que o algoritmo de regressão linear por MQO acha uma linha, plano ou hiperplano que passa entre os dados de forma que a distância quadrada entre os pontos e a linha, plano ou hiperplano seja minimizada. Vamos agora implementar esse algoritmo em Python. Para realmente entender a mecânica do algoritmo, vamos implementá-lo usando apenas Numpy, um pacote de computação numérica. Isso será feito apenas por motivos pedagógicos e, na prática, recomendo aplicar regressão linear partindo de uma implementação já existente. Para isso, veja o tutorial de regressão linear com Scikit-Learn.
import pandas as pd # para ler os dados em tabela
import numpy as np # para álgebra linear
from sklearn import linear_model, model_selection, datasets
import matplotlib.pyplot as plt # para fazer gráficos
from matplotlib import style
from time import time # para ver quanto tempo demora
np.random.seed(1) # para resultados consistentes
class linear_regr(object):
def __init__(self):
pass
def fit(self, X_train, y_train):
# adiciona coluna de 1 nos dados
X = np.insert(X_train, 0, 1, 1)
# estima os w_hat
# (X^T * X)^-1 * X^T * y
w_hat = np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)),X.T),y_train)
self.w_hat = w_hat
self.coef = self.w_hat[1:]
self.intercept = self.w_hat[0]
def predict(self, X_test):
X = np.insert(X_test, 0, 1, 1) # adiciona coluna de 1 nos dados
y_pred = np.dot(X, self.w_hat) # X * w_hat = y_hat
return y_predOk! Teoria justificada e algoritmo pronto. Vamos agora ver se ele consegue aprender os \( \hat{w_i}\) de dados reais. OBS: Os dados podem ser encontrados aqui.
data = pd.read_csv('../data/hprice.csv', sep=',').ix[:, :6] # lendo os dados
data.fillna(-99999, inplace = True) # preenchendo valores vazios
X = np.array(data.drop(['price'], 1)) # escolhendo as variáveis independentes
y = np.array(data['price']) # escolhendo a variável dependente
# separa em bases de treino e teste
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.3, random_state = 1)
data.head(5)| price | assess | bdrms | lotsize | sqrft | colonial |
|---|---|---|---|---|---|
| 300.0 | 349.1 | 4 | 6126 | 2438 | 1 |
| 370.0 | 351.5 | 3 | 9903 | 2076 | 1 |
| 191.0 | 217.7 | 3 | 5200 | 1374 | 0 |
| 195.0 | 231.8 | 3 | 4600 | 1448 | 1 |
| 373.0 | 319.1 | 4 | 6095 | 2514 | 1 |
Treinando, testando e comparando o regressor:
t0 = time()
regr = linear_regr()
regr.fit(X_train, y_train)
print("Tempo do criado manualmente:", round(time()-t0, 3), "s")
# medindo os erros
y_hat = regr.predict(X_test) # prevendo os preços
print('Média do erro absoluto: ', np.absolute((y_hat - y_test)).mean())
print('Média do erro relativo: ', np.absolute(((y_hat - y_test) / y_test)).mean())
# comparando com o de mercado
regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)
print("\n\nTempo do de mercado:", round(time()-t0, 3), "s")
# medindo os erros
y_hat = regr.predict(X_test) # prevendo os preços
w_hat = regr.intercept_
w_hat = np.append(w_hat, regr.coef_)
print('Média do erro absoluto: ', np.absolute((y_hat - y_test)).mean())
print('Média do erro relativo: ', np.absolute(((y_hat - y_test) / y_test)).mean())Tempo do criado manualmente: 0.097 s
Média do erro absoluto: 34.9234990043
Média do erro relativo: 0.122915533711
Tempo do de mercado: 0.254 s
Média do erro absoluto: 34.9234990043
Média do erro relativo: 0.122915533711
Nada mal... O preço previsto é, na média, apenas 12,2% diferente do preço real/observado. Note que o algoritmo aprendeu os parâmetros \( \hat{\pmb{w}}\) com uma parte dos dados e usou-os para prever dados que nunca tinha visto, mostrando uma boa capacidade de generalização.
Para comparação, utilizamos um modelo de regressão linear implementada no módulo Scikit-Learn, ao qual chamamos “de mercado”. O nosso algoritmo produz os mesmos resultados do de mercado, então podemos saber que não erramos nada. Além disso, o nosso algoritmo é mais rápido, mas essa diferença é insignificante, em termos práticos.
Considerações Finais
Eu considero o algoritmo de regressão linear como a base da ciência de modelagem estatística. Embora muito simples, regressão linear normalmente já te leva bem longe em termos de qualidade de previsão, enquanto os algoritmos de Aprendizado de Máquina mais complexos só fornecem uma melhora marginal em cima da qualidade adquirida com regressão linear. Assim sendo, termino com alguns conselhos práticos para usá-la.
- Quando tentar prever um valor contínuo - como preço, demanda, ou um índice qualquer - sempre comece usando regressão linear antes de tentar outros algoritmos de AM mais complexos.
- Regressão linear possibilita uma excelente interpretação dos parâmetros \( \hat{w_i}\) encontrados e pode ser por isso considerado um modelo caixa branca. Infelizmente, a capacidade interpretativa depende de um aprofundamento que não é a intenção desse tutorial. Caso queira se aprofundar no algoritmo, veja 1 ou 2.
- Regressão linear por MQO tem um processo de treinamento muuuuuito rápido. Mesmo com milhões de dados, é possível estimar os parâmetros em menos de um segundo. Além disso, uma vez treinado, o regressor ocupa muito pouco espaço, pois só armazena o vetor \( \pmb{\hat{w}}\). Há uma exceção, no entanto. Regressão linear da forma que vimos depende da inversão de uma matriz, o que pode começar a demorar muito quando temos muitas dimensões nos nossos dados - digamos mais de 10000. Nesse caso, recomenda-se algum tipo de redução de dimensionalidade antes de treinar o algoritmo, ou otimizar a função custo de maneira iterativa ao invés de analiticamente.
Vale uma nota de atenção: aqui só podemos abordar regressão linear brevemente. Ainda há problemas de inferência (saber se os coeficientes são estatisticamente significantes), de interpretação em outras escalas, de hipóteses assumidas e do que fazer quando tais hipóteses são violadas. Tenha isso em mente na hora de usá-lo! Muita coisa ficou incompleta aqui.











