Posted on 26/08/2017

Conteúdo

1. Motivação
2. Seleção Aleatória
3. Thompson Sampling
4. Referências

Motivação: Os Bandidos Bernoulli

Antes de procedemos com o algoritmo, vamos entender um dos problemas que ele se propõe a resolver. Segundo a literatura, máquinas caça-níqueis (ou slot machines) são conhecidas como “bandidos” por roubar o dinheiro de quem aposta nela. Imagine agora um cenário com \(n\) caça-níqueis, cada uma com uma distribuição de probabilidade de sucesso diferente. Um apostador se depara com essas máquinas sem saber qual delas lhe dará mais chances de ganhar dinheiro. Para descobrir isso, o apostador terá que testá-las puxando as alavancas. Durante o processo, ele terá que fazer um trade-off entre exploração e experimentação, isto é, entre puxar a alavanca da máquina que tem se mostrado a melhor durante seus experimentos e experimentar novas máquinas que possivelmente seriam melhores.

De maneira mais geral, esse problema é definido em termos de \(K\) ações, cada uma com uma probabilidade de sucesso \(\theta_k\) desconhecida, mas constante no tempo, podendo assim ser descoberta com experimentação. Além disso, cada experimento está associado a um custo, geralmente um custo de oportunidade definido em função da não exploração exclusiva da ação ótima. Esse tipo de cenário pode surgir em teste de layouts de site, teste de novas drogas, teste de propagandas, escolha de investimentos e até em testes de modelos de aprendizagem de máquina. Se você está familiarizado com testes A/B, sabe que eles também são situações de bandidos Bernoulli. Note como nessas situações temos sempre mais do que uma opção para testar e incorremos num custo para cada teste realizado. Assim, nos interessa descobrir o mais rápido possível qual a opção que gera mais sucessos para que possamos explorá-la e descartar as outras. Há outras versões do problema, em que podemos ter várias ações ótimas, dependendo do contexto, mas vamos ficar no caso mais simples aqui. Para informações mais detalhadas, sugiro este artigo da Wikipedia.

Seleção Aleatória

Uma forma bastante simples de solucionar o problema dos bandidos Bernoulli é testar cada bandido \(x\) vezes e depois simplesmente escolher aquele que teve a maior taxa de sucesso durante o experimento. Vamos chamar isso de política de seleção aleatória. Como exemplo, considere a tarefa de escolher entre dois modelos de classificação que performaram igualmente bem nos dados de teste.

Na política de seleção aleatória, mandamos ambos os modelos para produção e definimos um número de experimentos, digamos 20000 classificações. Durante este período de teste, selecionamos aleatoriamente um dos modelos para realizar cada classificação. Ao final do experimento, computamos a taxa de acerto de cada modelo e descartamos o que for pior. É bastante simples, então vamos à implementação!

Antes de qualquer coisa, vamos criar um simulador de modelos. Vamos utilizar a biblioteca NumPy aqui, apenas para gerar números aleatórios. A classe de modelo falso terá como único parâmetro a acurácia do modelo. Assim, um modelo falso criado com m = fakeModel(0.1) simulará um modelo que acerta em média, 10% das vezes. O método .score() da classe simula uma classificação do modelo.

import numpy as np

class fakeModel(object):
    def __init__(self, accuracy):   
        self.accuracy = accuracy # define a acurácia do modelo

    def score(self):
        if np.random.uniform(low=0.0, high=1.0, size=None) < self.accuracy:
            return 1 # simula um acerto
        else:
            return 0 # simula um erro

Agora vamos implementar a política de seleção aleatória. Essa classe aceitará uma lista de modelos falsos e o número de experimentos. O método .play() realizará a quantidade de experimentos pré-definida, selecionando aleatoriamente um dos modelos e computando sua previsão. Também vamos armazenar os acertos de cada modelo em uma lista num_1. Ao final dos experimentos poderemos saber qual dos modelos mais acertou e qual foi a acurácia da nossa política de seleção aleatória durante o experimento.

class randomSelection(object):
    def __init__(self, modelsList, nExper):
        self.modelsList = modelsList # define a lista de modelos
        self.nExper = nExper # define o número de experimentos

        self.num_1 = [0] * len(modelsList) # para armazenar acertos
        self.selectedMod = [0] * len(modelsList) # para armazenar seleções

    def play(self):
        right = 0
        for i in range(self.nExper): # itera pelos experimentos

            # escolhe modelo aleatoriamente
            modToPick = np.random.randint(0, len(self.modelsList)) 
            isRight = self.modelsList[modToPick].score()

            self.selectedMod[modToPick] += 1 # armazena seleção de modelos

            if isRight==1:
                self.num_1[modToPick] += 1 # armazena acerto

            right += isRight # adiciona número de acertos

        return 1.0 * right / self.nExper # retorna a acurácia da política

Para testar essa política de seleção aleatória de modelos vamos criar dois modelos falsos muito parecidos. O primeiro terá uma acurácia de 0.6 e o segundo, de 0.62. Procedemos normalmente com a política, selecionando um modelo aleatoriamente durante cada teste do experimento. Ao final, podemos simplesmente ver qual modelo acertou mais e descartar o outro.

Como estamos selecionando aleatoriamente os modelos durante o teste, podemos esperar que cada modelo seja escolhido para classificar as amostras 50% das vezes. Assim, a acurácia esperada do experimento é de \((0.6 + 0.62) / 2 = 0.61\). É importante ressaltar que num teste real nós não saberíamos esses valores e nosso objetivo seria justamente descobrir essas taxas de acerto.

m1 = fakeModel(0.6)
m2 = fakeModel(0.61)

rs = randomSelection([m1, m2], 20000)
print rs.play() # ~(.60 + .62) / 2 = 0.61
print rs.selectedMod # mostra quanto cada modelo foi selecionado
print rs.num_1

0.6093
[10114, 9886]
[6092, 6094]

Como esperado, o primeiro modelo tem uma taxa de acerto menor, de \(\frac{6092}{10114} = 0.6023\), enquanto que o segundo modelo acerta um pouco mais \(\frac{6094}{9886} = 0.616\). Além disso, acurácia do experimento como um todo é próxima de 0.61 (0.6093).

Com essa política de seleção aleatória conseguiríamos descobrir o melhor modelo, descartando aquele que não é ótimo. No entanto, isso vem a um custo, que é utilizar um modelo não ótimo para quase 10000 classificações. Isso pode não ser um problema se o custo de cada experimento for baixo, mas considere o caso de testar novas drogas para um câncer ou decidir qual ação comprar, onde cada classificação errada tem um custo altíssimo. Talvez a política de seleção aleatória não seja a melhor opção nesses casos. O ideal seria um algoritmo que, já durante o experimento, proativamente escolhesse a melhor ação com base nos seus erros e acertos passados.

Thompson Sampling

Thompson Sampling é um algoritmo de aprendizagem por reforço amplamente utilizado na indústria para resolver problemas de bandidos Bernoulli. Ele é especialmente atrativo devido a sua simplicidade, além de ser extremamente eficiente. Em um nível intuitivo, o algoritmo primeiro assume que todas as ações tem mesma probabilidade de ser a melhor, selecionando assim aleatoriamente. Conforme os retornos das ações vão sendo observados, o algoritmo ou agente atualiza sua crença sobre qual ação é a melhor e passa a selecionar novas ações de acordo com essa nova crença. Assim, no decorrer dos testes, o agente foca sua atenção nas melhores ações, diminuindo seu grau de incerteza sobre elas. Antes de prosseguir com os formalizamos matemáticos é interessante visualizar algumas iterações de Thompson Sampling. Para isso vamos usar uma animação retirada deste blog.

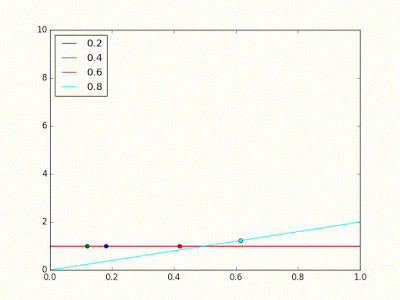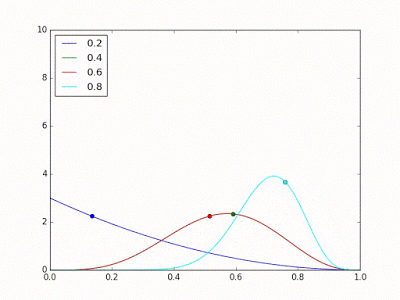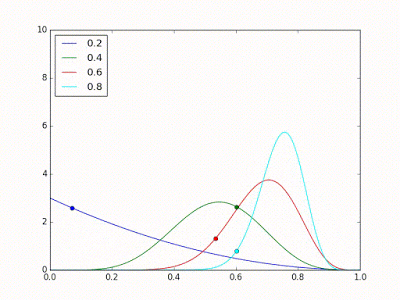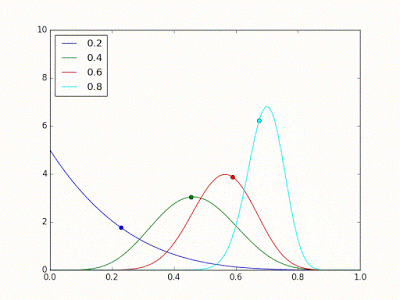
Considera que tenhamos 4 modelos, com acurácias desconhecidas 0.2, 0.4, 0.6 e 0.8. Nós então decidimos usar Thompson Sampling para descobrir qual é o melhor. Em algum momento do teste, as distribuições estimadas para cada modelo serão representadas pela imagem a seguir:

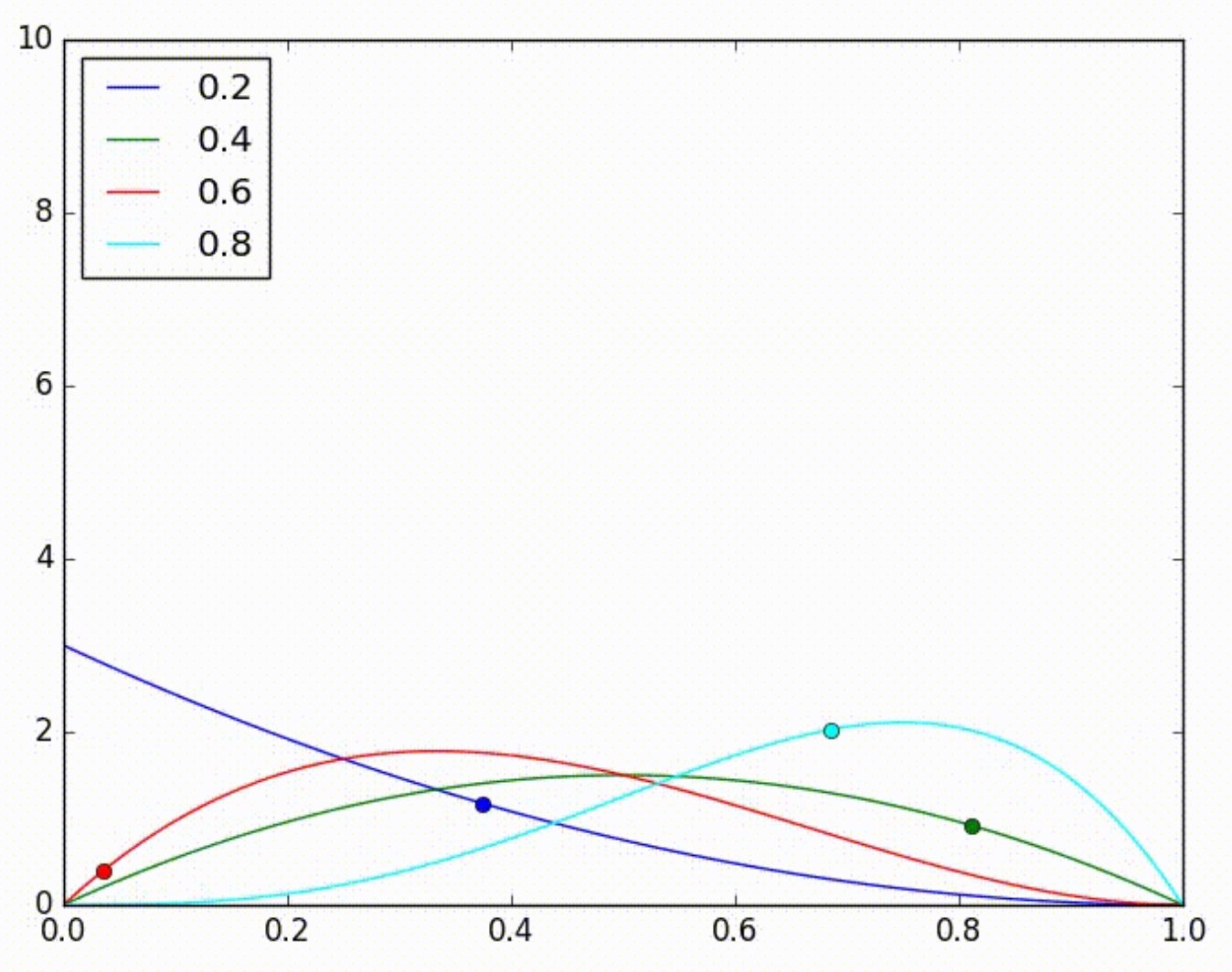
Na seguinte iteração, nós retiramos uma amostra aleatória de cada uma destas distribuições e, por acaso, a distribuição do modelo azul teve a maior amostra, como denotada pela bolinha azul na imagem abaixo. Então escolhemos esse modelo para realizar uma previsão e, por sorte, ele acerta. Isso faz com que a estimativa da sua distribuição seja ajustada para a direita, como mostra a seguinte imagem.

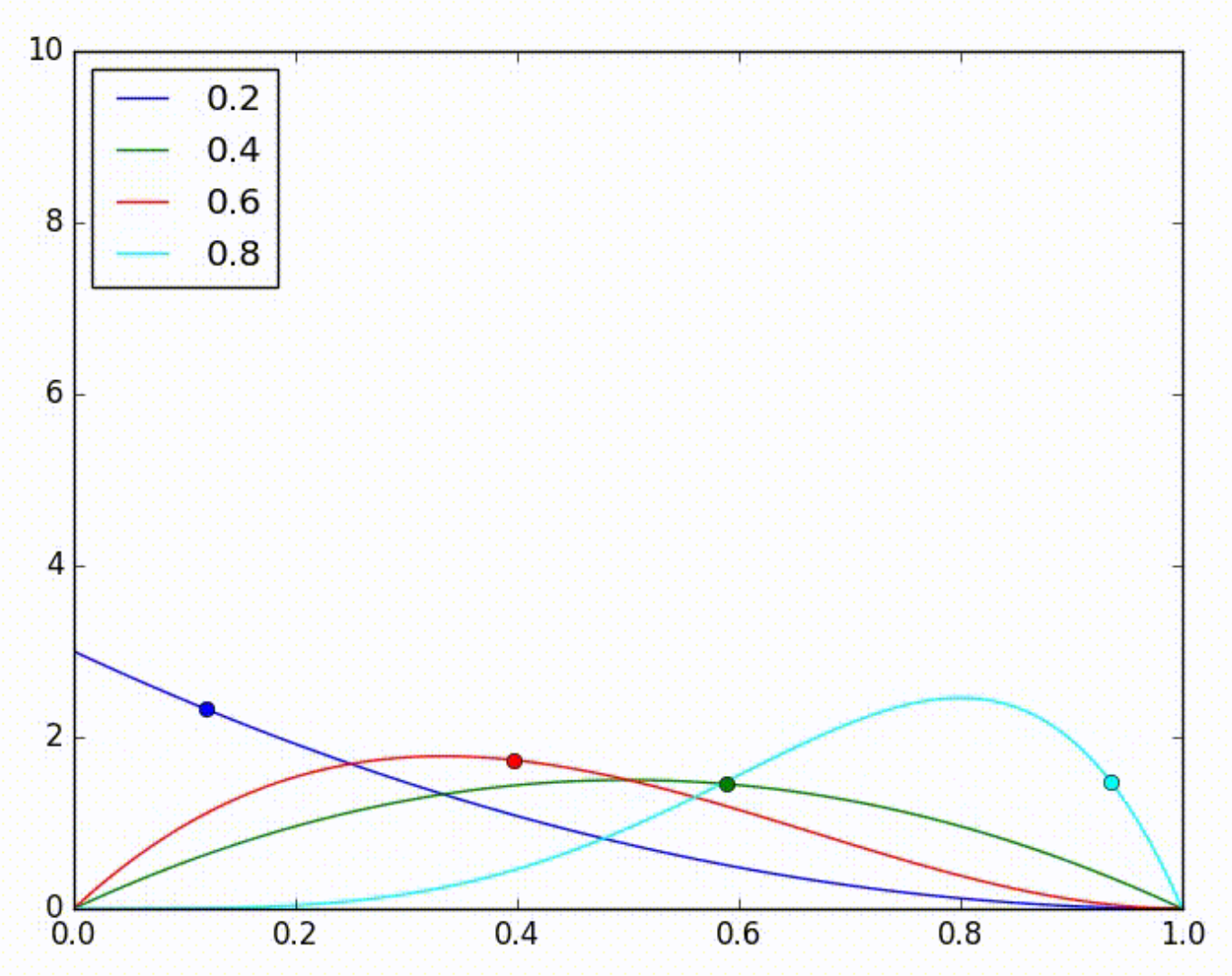
Novamente retiramos uma amostra aleatória de cada uma das distribuições estimadas e, novamente, por acaso a amostra azul tem o maior valor. Novamente, o modelo azul é escolhido para fazer a classificação, mas desta vez, por azar, ele erra. Isso ajusta a estimativa da sua distribuição para a esquerda, como na imagem abaixo.

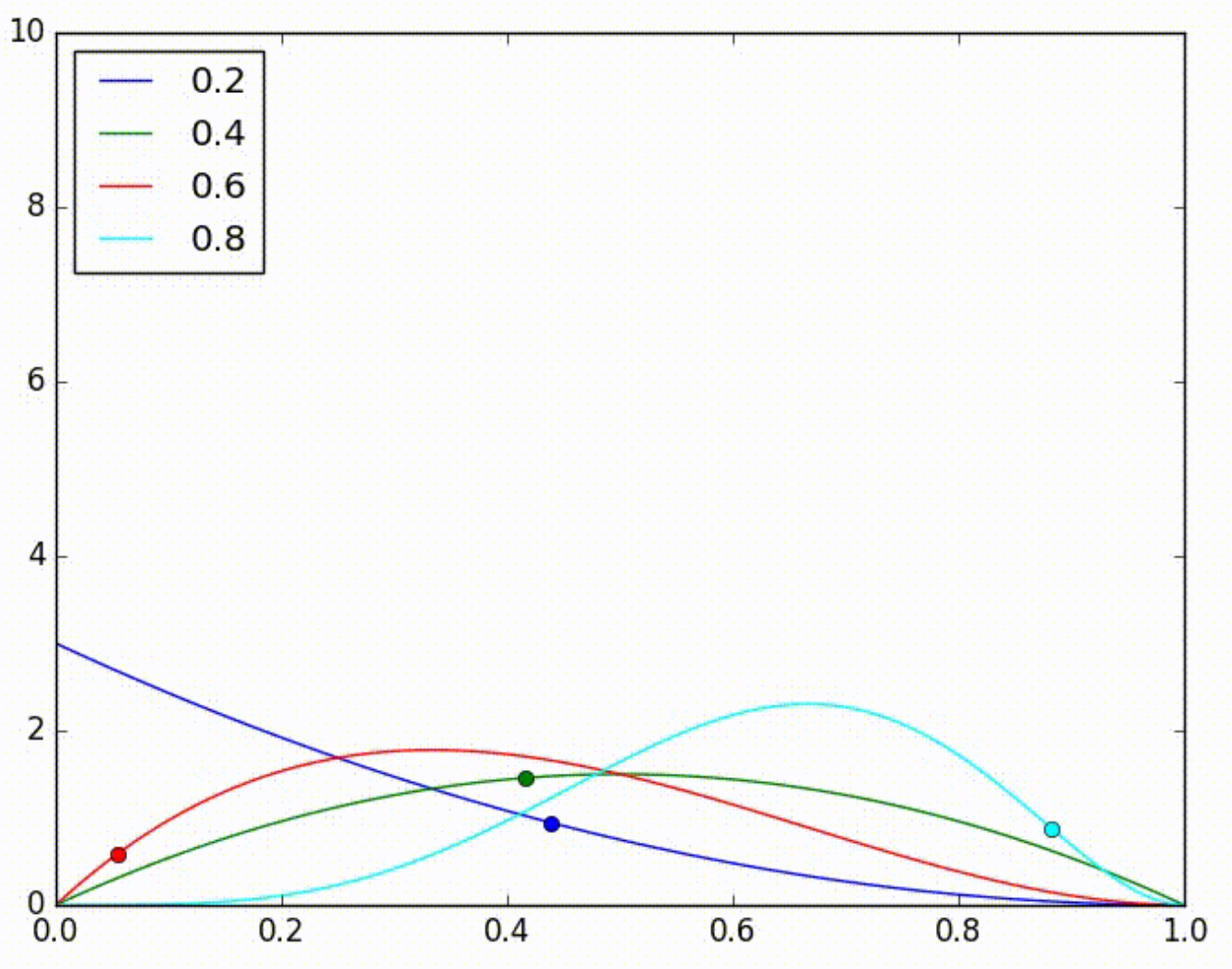
Agora, quando retiramos mais uma vez uma amostra de cada distribuição estimada, por acaso a amostra do modelo verde é a maior de todas. Mas, quando selecionamos esse modelo, ele erra a previsão, causando um ajuste para a esquerda da estimativa de sua distribuição, como mostrado na imagem abaixo.

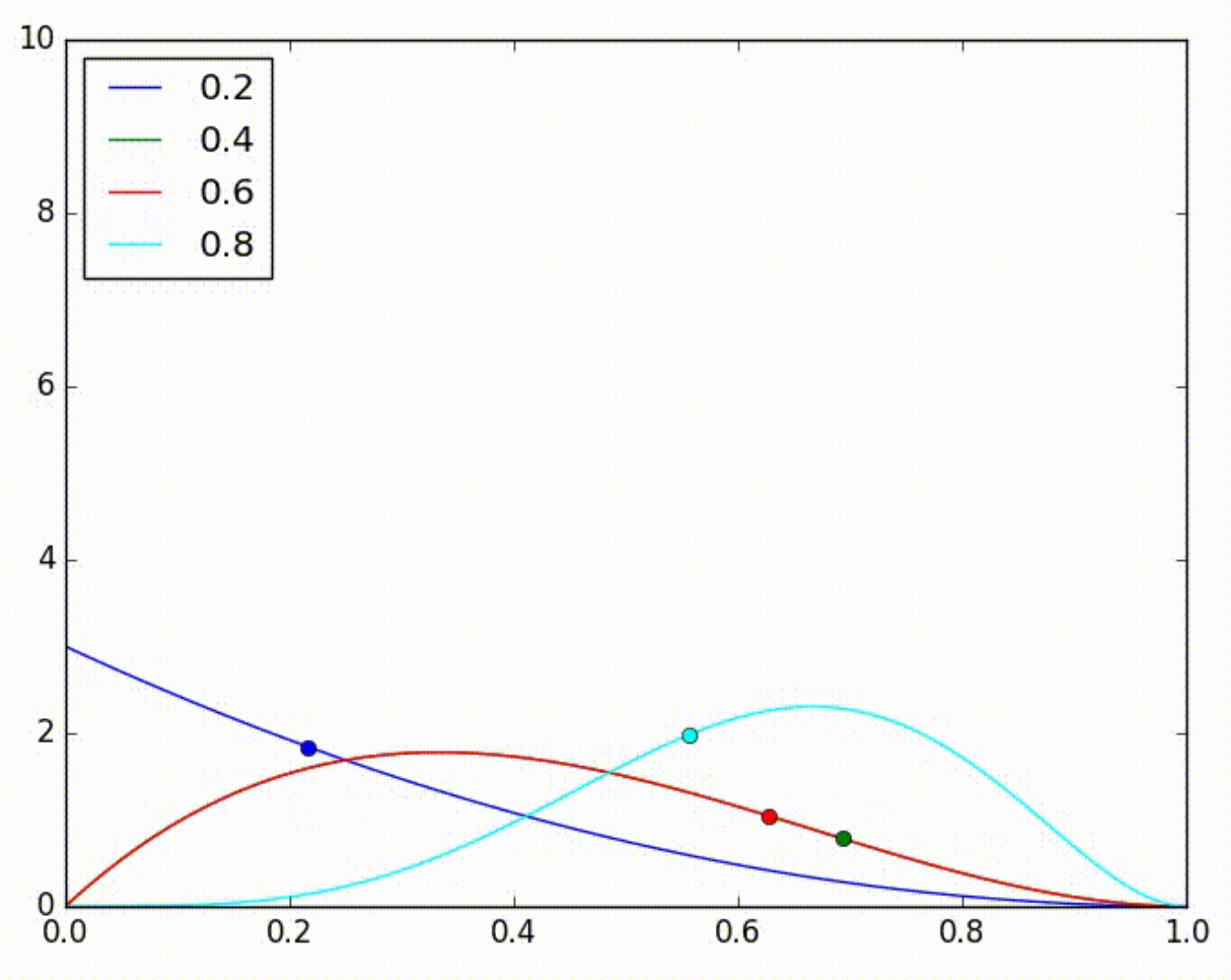
O que é importante perceber acima são os 3 passos de cada iteração. 1) retirar uma amostra de cada distribuição estimada, 2) escolher o modelo com a maior amostra e 3) ajustar as estimativas da distribuição do modelo escolhido com base no acerto ou erro desse modelo. Além disso, na prática, o que acontece é que ações piores são menos exploradas e, por conta disso, sua distribuição fica mais larga, refletindo maior incerteza sobre elas. Por outro lado, por serem constantemente escolhidas, ações melhores tendem a ter distribuição mais estreita em torno do seu retorno real, diminuindo a incerteza em trono delas. Intuitivamente, podemos dizer que Thompson Sampling não gasta tempo experimentando ações que não se mostram promissoras, focando mais em explorar a ação que parece ótima e experimentar apenas as que tem alguma chance de sê-lo. Segue a animação completa do aprendizado de Thompson Sampling do blog de Michael Elkan. Repare como as distribuições mais atualizadas são as dos melhores modelos.

Mais formalmente, cada ação \(k\) está associada a um vetor de recompensas \(\pmb{y}\), que é dado por uma distribuição de probabilidade Bernoulli \( p(\pmb{y} | \theta_k) \sim \mathcal{B}(\theta_k)\). \(\theta_k\) é desconhecido pelo agente e essa incerteza é iniciada assumindo uma distribuição uniforme \(p(\theta_k) \sim \mathcal{U}[0,1]\). Conforme o experimento se desenrola, atualizamos a estimativa de \(\theta_k\) segundo a regra de Bayes:

Como cada experimento é parametrizado por uma Bernoulli, podemos reescrever a regra acima em termos de distribuições binomiais com \(i\) sucessos em \(n\) testes.

E essa formula complexa pode ser simplificada para algo bem mais amigável como a distribuição beta.

A distribuição beta faz sentido intuitivo, tendo seu pico em \(\theta_k= \frac{i}{n}\), que é simplesmente a contagem empírica de sucessos ao se escolher a ação \(k\), dividido pelo total de ações tomadas \(n\). O algoritmo procede então retirando uma amostra desta distribuição para cada escolha possível, escolhendo a ação com maior valor de beta e atualizando \(i\) conforme tal ação gera um erro ou um acerto. Podemos formalizar Thompson Sampling em quatro passos:

1. Para cada teste \(n\), considerar, para cada ação, o número de acertos (\(i_1\)) e erros (\(i_0\)) que ela teve até o teste \(n\).
2. Para cada ação, retirar uma amostra que servirá de estimação para \(\theta\), \(\hat{\theta_k} = \beta(i_{k1} + 1, i_{k0} + 1)\).
3. Selecionar a ação com maior \(\hat{\theta}\)
4. Atualizar (\(i_{k1}\)), se a ação for bem sucedida, ou (\(i_{k0}\)), caso contrário.

OK, já basta de teoria. Vamos à implementação! A classe thompsonSampling tem os mesmos parâmetros de inicialização da política de seleção aleatória, isto é, uma lista de modelos falsos e o número de experimentos. Além disso, vamos manter a contagem de números de acertos e erros para cada modelo, assim como uma lista que armazena o número de vezes que cada modelo foi selecionado durante o teste. Aqui, em vez de selecionar aleatoriamente os modelos para classificação, vamos criar uma lista que tenha, para cada modelo, uma amostra da distribuição beta parametrizada com \(\alpha\) sendo o número de acertos do modelo mais 1 e \(\beta\) sendo o número de erros do modelo mais 1. Escolheremos para classificação o modelo com a maior dessas amostras beta. Por fim, a atualização da distribuição é feita incrementando as contagens de acertos e erros do modelo.

class thompsonSampling(object):
    def __init__(self, modelsList, nExper):
        self.modelsList = modelsList
        self.nExper = nExper

        self.num_1 = [0] * len(modelsList) # armazena acertos por modelo
        self.num_0 = [0] * len(modelsList) # armazena erros por modelo
        self.selectedMod = [0] * len(modelsList) # armazena seleção por modelo

    def play(self):
        right = 0 # inicia a contagem de acertos totais no experimento
        # itera pelos experimentos
        for i in range(self.nExper):
            
            # para cada modelo, retira uma amostra da distribuição beta correspondente
            modBetas = [np.random.beta(self.num_1[mod] + 1, self.num_0[mod] + 1) for mod in range(len(self.modelsList))]            
            
            modToPick = np.argmax(modBetas) # escolhe o modelo com maior amostra beta

            # usa o modelo para realizar uma classificação e verifica se ele acerta
            isRight = self.modelsList[modToPick].score() 
            
            # aumenta a contagem de vezes que o modelo foi escolhido
            self.selectedMod[modToPick] += 1 
            
            # atualiza a contagem de erros e acertos do modelo
            if isRight==1:
                self.num_1[modToPick] += 1
            else:
                self.num_0[modToPick] += 1

            right += isRight # atualiza o total de acertos totais 

        # retorna a acurácia do experimento
        return 1.0 * right / self.nExper

Para testar esse algoritmo vamos usar novamente os dois modelos falsos, com acurácias desconhecidas de 0.60 e 0.62. Então aplicamos Thompson Sampling para descobrir qual desses modelos é o melhor.

ts = thompsonSampling([m1, m2], 20000)
print ts.play()
print ts.selectedMod
print ts.num_1

0.6221
[166, 19834]
[84, 12358]

Desta vez, o primeiro modelo tem uma taxa de acerto de \(\frac{84}{166}=0.506\), que é bem menor do que a sua acurácia real. O segundo modelo, por sua vez, tem uma taxa de acerto de \(\frac{12358}{19834}=0.623\), que é bem próxima da sua acurácia real. Além disso, note como o primeiro modelo foi selecionado apenas 166 vezes. Isso mostra que o algoritmo de Thompson Sampling descobriu rapidamente que ele não era ótimo e parou de experimentá-lo, focando mais em explorar o modelo ótimo. Note também que há um certo grau de erro estimativa da acurácia do primeiro modelo. Isso é esperado devido às poucas vezes que ele foi selecionado. Por fim, repare como a acurácia do experimento como um todo é bem próxima da acurácia do modelo ótimo. Isso mostra que, além de ser capaz de encontrar o melhor modelo, Thompson Sampling fez isso rápido o suficiente para que não precisássemos incorrer em custos desnecessário por escolher uma ação não ótima durante o experimento. É importante destacar que Thompson Samplsing é um algoritmo estocástico, então os seus resultados provavelmente serão um pouco diferentes dos meus.

Referências

A principal referência para esta postagem é o artigo de Russo et al, A Tutorial on Thompson Sampling, publicado mês passado. Também utilizei bastante conteúdo do post de Michael Elkan. Por fim, o código é adaptado do curso de Machine Learning A-Z.