Posted on 22/06/2017
Introdução
Redes Adversárias Geradoras (RAGs) são um tópico bastante avançado em aprendizado de máquina. Mais do que isso, elas introduzem um novo paradigma de treinamento de redes neurais e tem gente importante apostando nelas como o progresso mais estarrecedor que tivemos nos últimos dez anos em aprendizado de máquina.
Quando redes adversárias aparecem em materiais didáticos (o que é raro), geralmente é no último capítulo. Mesmo assim, eu decidi colocá-las aqui, como material introdutório, por alguns motivos. Em primeiro, RAG é uma tecnologia de ponta extremamente interessante e creio apresentá-las agora te incentivará a continuar aprendendo. Em segundo lugar, RAGs, embora matematicamente complexas, são extremamente simples de entender e de implementar. Assim, não se preocupe se a teoria por de trás delas não parecer muito clara a primeira vista; isso é normal. Por fim, na parte de implementação, RAGs serão um excelente treino para consolidar o que vimos [1] [2] sobre programação de redes neurais com TensorFlow.
Pré-requisitos
Se você só quer entender a intuição por traz de redes adversárias geradoras e por que elas são tão legais, siga adiante, sem medo, pela sessão intuitiva deste tutorial. No entanto, se você quer conseguir implementar RAGs, vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.
Intuição
Começamos com uma história (obviamente apócrifa). Imagine que Leonardo DiCaprio seja um falsificador de cheques bancários e que Tom Hanks seja um agente bancário (sim, a história é um pouco diferente) que precisa diferenciar cheques autênticos dos falsos produzidos por Leonardo DiCaprio. Pensemos agora nisso como um jogo: a cada rodada, Leonardo DiCaprio produz um punhado de cheques falos e Tom Hanks tenta os identificar. Cada cheque falso identificado gera pontos para Tom e diminui os pontos de Leonardo; por outro lado, cheques verdadeiros identificados como falsos diminuem os pontos de Tom. Por fim, cada cheque falso não identificado por Tom diminui sua pontuação e aumenta a de Leonardo. Note que cada ganho de Leonardo gera, necessariamente, uma perda para Tom. Chamamos esse tipo de jogo de soma zero, pois os ganhos de um jogador anulam os do outro, zerando a pontuação agregada do jogo.
Se colocarmos Tom e Leonardo para jogar esse jogo por muito tempo, devemos esperar que ambos fiquem muito bons nele. Como consequência, os cheques produzidor por Leonardo seriam indistinguíveis dos reais para nós, pessoas ignorantes; apenas o experiente Tom seria capaz de identificá-los.
O modelo de redes adversárias geradoras funciona exatamente como o jogo descrito acima. Nele, criamos duas redes neurais, uma geradora e uma discriminadora. À essa, damos o objetivo de distinguir entre dados reais e falsificadas; àquela, damos o objetivo de enganar a discriminadora, isto é, de gerar dados que se pareçam com a realidade. Por fim, treinamos as duas redes neurais em conjunto, até que a rede discriminadora não consiga mais do que 50% de acerto e a geradora produza exemplos parecidos com os dados reais.

Mas para que servem essas redes adversárias geradoras (ou RAGs)? Em primeiro lugar, podemos utilizar a rede geradora como uma fonte inesgotável de criatividade. Por exemplo, poderíamos treinar RAGs em modelos 3D de móveis e depois utilizar a geradora como uma inteligência artificial para design de mobília (isso inclusive já foi feito). Em segundo lugar, modelos gerativos como esse tem consequências filosóficas. De forma bem simplificada, no debate entre dualismo (a visão de que somos corpo e mais alguma coisa) e materialismo (a ideia de que somos apenas corpo e de que a consciência é apenas consequência de um maquinário complexo), os dualistas perdem o argumento da criatividade como algo que nos distingue do puramente mecânico (a menos que estejam dispostos a admitir que redes neurais também são mais do que apenas mecânicas). Por fim, se você entende um pouco de probabilidade e cálculo, deve saber que modelar probabilidade de dados é algo extremamente difícil de ser feito, pois envolve estimar uma integral impossível de se computar. Assim, é bastante interessante ter uma rede neural que pode facilmente fornecer amostras da distribuição dos dados sem precisar lidar com uma integral complicada.
Para mais exemplos divertidos de aplicações, verifique [1], [2] ou [3].
Mecânica do Modelo Matemático
Vamos agora ver mais a fundo a teoria por trás das redes adversárias geradoras. A partir desse ponto, o conteúdo se tornará mais complicado, técnico e matemático. Se a você só interessa uma breve intuição do que são RAGs, ou se você não acompanhou os tutoriais passados, sugiro que pare de ler aqui. Mesmo aqueles que já com certo conhecimento em matemática e aprendizado de máquina verão que RAGs são mais complexas do que as redes neurais tradicionais. RAGs são extremamente recentes e na fronteira do conhecimento; ainda não sabemos como torná-las simples. Se você não entender tudo da formulação matemática, não se preocupe. Quando chegarmos na implementação, tudo ficará extremamente claro e mais simples.
Em primeiro lugar, gostaria de destacar que RAGs são modelos de aprendizado não supervisionado, já que nosso objetivo não é realizar nenhum tipo de previsão, mas entender a estrutura dos dados. Redes adversárias geradoras foram propostas por Goodfellow et al. em um artigo chamado Generative Adversarial Networks, 2014. RAGs são um tipo de rede geradora diferenciável, isto é, que podemos usar backpropagation para treinar com gradiente descendente. Esse tipo de modelo transforma amostras de um vetor latente \(\pmb{z}\) em amostras \(\pmb{x}\) usando uma função diferenciável \(g(\pmb{z}, \pmb{\theta})\). Essencialmente, redes geradoras diferenciáveis são procedimentos computacionais para gerar amostras (Goodfellow et al, 2016).
Redes adversárias geradoras são modelos baseados em teoria dos jogos, o que os torna especialmente interessantes para um economista. Apenas para introduzir o tema, teoria dos jogos é um campo da matemática aplicada que modela situações de interações estratégicas, isto é, quando as decisões de um agente influenciam nas recompensas e nas ações de outros agentes. O campo se expandiu consideravelmente com noção de equilíbrio desenvolvida por John Nash, usada extensamente em microeconomia para entender funcionamento de carteis, inflação inercial, exaustão do meio ambiente, leilões, contratos e muitos outros temas.
Como já vimos acima, no jogo de RAGs, a rede gerativa tenta produzir amostras que se assemelhem com os dados originais, \(\pmb{x}\sim P_{dados}\), de acordo com uma série de transformações que pode ser descrita por uma função \(\pmb{x}=g(\pmb{z};\pmb{\theta}_g)\). A rede discriminadora, por sua vez, produz a probabilidade de \(\pmb{x}\) ser falso ou real, que é dado por uma função \(d(\pmb{x};\pmb{\theta}_d)\). Na sua forma mais simples, dados os dois jogadores (discriminadora e gerador), o problema de aprendizado de RAGs é formulado como um jogo de soma zero, no qual uma função \(r(\pmb{\theta}_d;\pmb{\theta}_g)\) determina a recompensa (pay-off) de uma das redes e \(-r(\pmb{\theta}_d;\pmb{\theta}_g)\), da outra. Como o jogo é de soma zero, no único equilíbrio de Nash teríamos
\[g^* = \arg \min_{g} \max_{d} r(g, d)\]em que \(g^*\) é a rede geradora no ponto de convergência, capturando de forma ótima a distribuição dos dados. A escolha padrão para \(r\) é
\[r(\pmb{\theta}_d;\pmb{\theta}_g) = \mathbb{E}_{x\sim Pdados}log(d(\pmb{x})) + \mathbb{E}_{x\sim Pmodelo}log(1 - d(\pmb{x}))\]que não é nada mais do que uma forma um pouco mais complicada de escrever a função custo de entropia cruzada, apresentada no tutorial de regressão logística. Agora, com uma notação mais simples, podemos separar a função custo de cada uma das redes. Para a discriminadora teríamos
\[L_d = -\frac{1}{m} \sum[ log(d(\pmb{x})) + log(1 - d(g(\pmb{z})))]\]Note que o segundo termo em \(log\) dentro da soma diz respeito aos erros de classificação das amostras falsas. Tendo isso em mente, fica mais fácil ver que o custo a ser otimizado pela rede gerativa é dado por
\[L_g = \frac{1}{m} \sum[log(1 - d(g(\pmb{z})))]\]Intuitivamente, essas funções custo colocam como objetivo da rede discriminadora maximizar os acertos de classificação de amostras em falsas e verdadeiras; a rede geradora simplesmente tentará minimizar esses acertos. Mais ainda, no ponto de convergência, a recompensa das duas redes é a mesma e a rede discriminadora não consegue distinguir falsos e verdadeiros com mais sucesso do que chutes aleatórios, isto é, ela aponta todos os exemplos como tendo 50% de chance de serem falsos.
Desafios
Na prática, treinar RAGs é extremamente difícil devido a não convexidade de \(\max_{d} r(g, d)\). Além disso, equilíbrios de Nash em jogo de soma zero não são pontos de mínimo, mas de sela, isto é, são pontos de mínimo com respeito aos parâmetros de um jogador, mas de máximo com respeito aos parâmetros de outro jogador. Assim, é comum que RAGs fiquem orbitando em torno desse ponto de sela e sofrer com subajustamento. Além disso, é possível identificar pelo menos duas situações claras em que o treinamento de RAGs pode falhar:
- Se o custo do discriminador chegar próximo de zero, o custo da rede gerativa se aproxima do infinito e quase não há gradiente para a otimização da geradora.
- No outro extremo, se o custo da discriminadora for muito alto, também não quase haverá gradiente para a otimização da geradora.
Isso faz com que RAGs sejam bastante instáveis e sofram com sub ajustamento. Para que possa haver convergência (ou algo próximo disso), é preciso que a performance das duas redes seja pareado durante o treinamento. Hoje, isso ainda é feito principalmente com um ajuste cuidadoso dos hiperparâmetros, mas pode ser que no futuro encontremos melhores formas de treinar RAGs.
Implementação
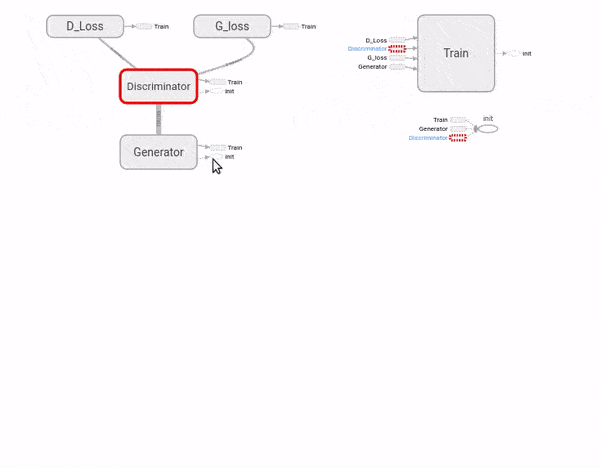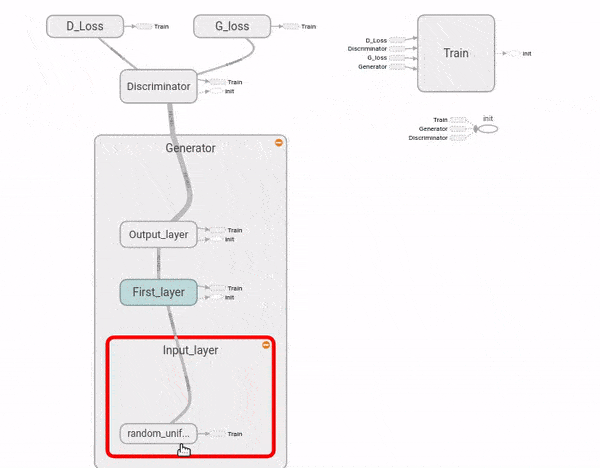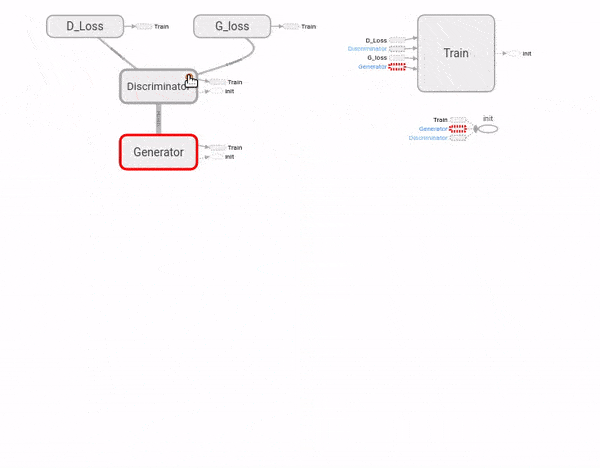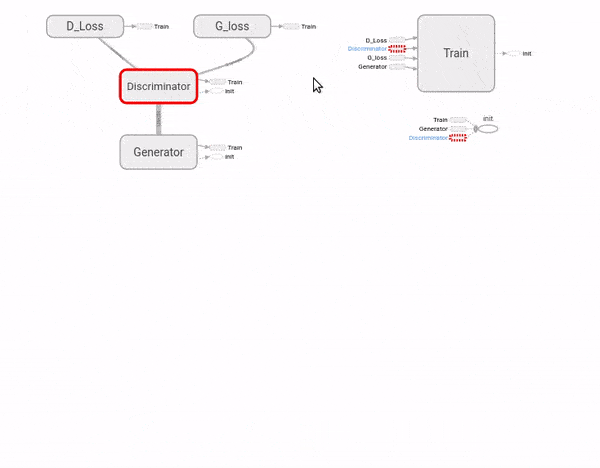
Vamos implementar uma RAG como acima. Ela não será capaz de imaginar novos design para móveis, nem nada muito complicado. Mais uma vez, vamos utilizar a base de dados MNIST de dígitos escritos à mão. Nosso objetivo será criar e treinar uma RAG extremamente simples para gerar dígitos parecidos com os escritos por um humano.
import numpy as np # para computação numérica menos intensiva
import os # para criar pastas
import tensorflow as tf # para redes neurais
# criamos uma pasta para salvar o modelo
if not os.path.exists('tmp'): # se a pasta não existir
os.makedirs('tmp') # cria a pasta
# criamos uma pasta para visualização no TensorBoard
if not os.path.exists('logs'):
os.makedirs('logs')
# baixa os dados na pasta criada e carrega os dados
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("tmp/")Agora, vamos definir algumas constantes, dentre as quais estarão os hiperparâmetros do nosso modelo. As nossas imagens são 28 por 28 pixeis, mas vamos usar a versão achatada delas, com uma única linha de 784 (28*28) pixeis. A rede geradora terá em sua camada de entrada um vetor aleatório \(\pmb{z}\), que terá dimensão 100. Ela passará esse vetor por uma camada oculta com 128 neurônios e então, a partir desses neurônios, criará uma imagem de 784 pixeis.
A discriminadora, por sua vez, pegará um lote com imagens reais e geradas pela geradora. Ela passará essas imagens por 128 neurônios e então produzirá a probabilidade de cada imagem ser real ou falsa.
# definindo constantes
n_iter = 30000 # número de iterações de treino
batch_size = 128 # tamanho do mini-lote
n_image = 784 # pixeis na imagem (28*28)
# Geradora
z_shape = 100 # tamanho do vetor z latente
n_Ghl1 = 128 # neurônios da geradora
# Discriminadora
n_Dhl1 = 128 # neurônios da discriminadora
n_outputs = 1 # número de variáveis dependentesOK, tudo muito fácil até agora. Vamos então criar nossa RAG. A primeira vista, o código a seguir pode parecer bem mais complexo do que as redes neurais simples que criamos até agora. No entanto, novamente, não há nada além do que já vimos: criar e empilhar camadas! Além disso, ele contém elementos importantes do tutorial passado, como escopos de nome organizando as camadas e nós de resumo para visualização no TensorBoard. Acredito então que entender esse grafo será um excelente exercício. Note como vamos organizar nosso código TensorFlow em dois escopos de nome principais, o da rede geradora e o da rede discriminadora. A explicação do grafo vem após o código.
# começamos montando nossa rede geradora
with tf.name_scope('Generator'):
# Camada de entrada
with tf.name_scope('Input_layer'):
# vetor latente aleatório
z = tf.random_uniform([batch_size, z_shape], minval=-1, maxval=1)
# Primeira Camada
with tf.name_scope('First_layer'):
# cria as variáveis da camada
G_W1 = tf.Variable(tf.truncated_normal([z_shape, n_Ghl1]))
G_b1 = tf.Variable(tf.zeros(shape=[n_Ghl1]))
# multiplicação de matriz seguida de não linearidade ReLU
G_h1 = tf.nn.relu(tf.matmul(z, G_W1) + G_b1)
# Camada de saída
with tf.name_scope('Output_layer'):
# Cria as variáveis da camada
G_W2 = tf.Variable(tf.truncated_normal([n_Ghl1, n_image]))
G_b2 = tf.Variable(tf.zeros(shape=[n_image]))
# cria a imagem falsa com uma transformação linear
# e como os pixeis são entre 0 e 1, usamos a sigmoid
fake_images = tf.nn.sigmoid(tf.matmul(G_h1, G_W2) + G_b2)
# para visualização no TensorBoard. Seleciona 8 imagens para salvar.
img_summ = tf.summary.image('Generated_images',
tf.reshape(fake_images, [-1, 28, 28, 1]), 8)
# junta as variáveis da geradora em uma lista
G_vars = [G_W1, G_W2, G_b1, G_b2] Diferentemente de problemas que vimos até agora, a rede geradora não precisa de um tf.placeholder para receber dados. Isso porque ela apenas retira uma amostra de um vetor aleatório \(\pmb{z}\) e o converte em uma imagem. Assim, a camada de entrada da rede geradora será \(\pmb{z}\). A camada oculta é bem tradicional: uma transformação linear, seguida da não linearidade ReLU. Por fim, na camada de saída, não teremos o vetor de probabilidades, mas sim uma imagem. Com uma transformação linear, a rede geradora transformará os neurônios da sua camada oculta nessa imagem. Já que as imagens da nossa base de dados são representadas por pixeis com valores de 1 a 0, vamos usar a função logística na imagem gerada para achatar o valor dos pixeis para esse intervalo. Vamos usar o TensorBoard para visualizar as imagens geradas, então adicionamos um nó de resumo com tf.summary.image e passamos a ele a imagem gerada, após reformatá-la para 28 por 28 pixeis com tf.reshape. Por fim, colocamos todas os pesos (\(\pmb{W}\)) e vieses (\(\pmb{b}\)) da rede geradora em uma lista. Isso será útil quando quisermos treiná-la sem treinar a discriminadora junto.
Veremos agora como fica nossa rede descriminadora.
# agora, montamos a rede discriminadora
with tf.name_scope('Discriminator'):
with tf.name_scope('Input_layer'):
# placeholder para alimentar imagens reais
real_images = tf.placeholder(tf.float32, shape=[batch_size, n_image])
# empilha imagens falsas e reais em um único mini-lote
images = tf.concat([real_images, fake_images], 0)
# placeholders para colocar os alvos
labels = tf.concat([tf.zeros([batch_size, 1]), # reais
tf.ones([batch_size, 1])], 0) # falsas
# primeira camada
with tf.name_scope('First_layer'):
# cria as variáveis
D_W1 = tf.Variable(tf.truncated_normal([n_image, n_Dhl1]))
D_b1 = tf.Variable(tf.zeros(shape=[n_Dhl1]))
# aplica transformação linear seguida de não linearidade ReLU
D_h1 = tf.nn.relu(tf.matmul(images, D_W1) + D_b1)
# camada de saída
with tf.name_scope('Output_layer'):
# cria variáveis da camada
D_W2 = tf.Variable(tf.truncated_normal([n_Dhl1, 1]))
D_b2 = tf.Variable(tf.zeros(shape=[1]))
# tranformação linear para gerar o logit
D_logit = tf.add(tf.matmul(D_h1, D_W2), D_b2, name='D_logit')
# junta as variáveis da descriminadora em uma lista
D_vars = [D_W1, D_W2, D_b1, D_b2]A nossa rede discriminadora será uma rede neural bem simples, com uma única camada oculta e exatamente igual às que vimos nos tutoriais passados. A única coisa mais complicada nela é a camada de entrada, na qual juntamos o placeholder das imagens reais com as imagens falsas, produzidas pela geradora. Também vamos criar o vetor \(y\) de alvos dessa rede sem um placeholder, empilhando um vetor de \(0\) para representar as imagens reais e um vetor de \(1\) para representar as imagens falsas.
Quanto aos custos a serem minimizados, o da discriminadora é a tradicional entropia cruzada, a mesma que viemos usando até agora em problemas de classificação. Como só temos duas classes possíveis (0 para imagens reais e 1 para imagens falsas), não precisamos usar a função softmax e vamos usar tf.nn.sigmoid_cross_entropy_with_logits(...) para ter o custo calculado com a sigmoide.
# Custo da rede discriminadora
with tf.name_scope('D_Loss'):
# o custo é simplesmente a entropia cruzada, como em um problema de classificação tradicional
D_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit, labels=labels))
D_summ = tf.summary.scalar('D_loss', D_loss) # para o TensorBoard
# Custo da rede geradora
with tf.name_scope('G_loss'):
# o objetivo da geradora é fazer com que a previsão da geradora seja 0 nas falsas
G_loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit, labels=tf.zeros_like(D_logit))
# G só deve ter custo com as falsas, classificadas com reais
G_loss = G_loss * labels # zera custo das imagens reais.
G_loss = tf.reduce_mean(G_loss)
G_summ = tf.summary.scalar('G_loss', G_loss) # para TensorBoardOs erros da geradora serão os acertos da discriminadora, então podemos também usar o custo de entropia cruzada nos logits da discriminadora, só que agora a rede será penalizada quando a discriminadora prever algo diferente de 0 para as imagens falsas, isto é, quando a discriminadora acertar sua previsão. Não queremos que os erros da discriminadora nas imagens reais afetem o custo da geradora, por isso, vamos usar um pequeno truque. Não foi por acaso que decidi codificar as imagens reais como 0 e as falsas como 1. Já que temos essa codificação, podemos pegar o vetor de resposta do problema da discriminadora e multiplicar pelo vetor de custos da geradora. Como as imagens reais são codificadas com zero, essa operação zerará qualquer custo proveniente dessas imagens.
Agora, para o treino.
with tf.name_scope('Train'):
# otimizador para minimizar os custos
D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list=D_vars)
G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list=G_vars)
# para iniciar as variáveis
init = tf.global_variables_initializer()
# para registrar na visualização
loss_summ = tf.summary.merge([G_summ, D_summ])
file_writer = tf.summary.FileWriter('logs', tf.get_default_graph())Finalmente, adicionamos os nós de otimização. Note que serão dois: um para otimizar com respeito às variáveis da geradora e um para otimizar com respeito às variáveis da discriminadora. Adicionamos então um nó para iniciar as variáveis e para escrever no TensorBoard e terminamos nossa fase de construção.
Hora de executar o grafo criado acima! Para treinar nossa RAG, abrimos uma sessão no TensoFlow e iniciamos as variáveis do modelo. O loop de treinamento não tem nada de especial. Primeiro, pegamos um punhado (mini-lote) de imagens reais. Depois, executamos uma iteração de treino para ambas as redes. Para isso, colocamos as imagens reais no seu devido placeholder. A cada 100 iterações, vamos salvar o resumo dos custos da geradora e discriminadora; a cada 1000 passos, vamos salvar algumas imagens produzidas pela rede geradora. Nessa última execução, como não estamos usando a discriminadora, não precisamos passar as imagens reais para o placeholder de imagens.
with tf.Session() as sess:
sess.run(init) # iniciamos as variáveis
for step in range(n_iter+1):
# pega algumas imagens reais
X_img, _ = mnist.train.next_batch(batch_size)
# executa uma iteração de treino
_, _, summaries_str = sess.run([D_solver, G_solver, loss_summ],
feed_dict={real_images: X_img})
# salva o custo a cada 100 iterações
if step % 100 == 0:
file_writer.add_summary(summaries_str, step)
# salva algumas imagens geradas a cada 1000 passos
if step % 1000 == 0:
img_log = sess.run(img_summ)
file_writer.add_summary(img_log, step)
Resultados
Os resultados podem ser vistos acima. Note como, no começo do treinamento, a RAG produz apenas ruído. Conforme o treinamento acontece, as imagens geradas se aproximam mais e mais com dígitos escritos a mão. Eventualmente, as imagens geradas se assemelham todas a uns. Isso significa que o treinamento colapsou. Ou a geradora descobriu que produzir uns é um atalho para enganar a discriminadora facilmente, ou a discriminadora está com um custo muito baixo. Para saber qual é o caso, podemos ver o custo de ambas as redes para ver qual delas está ganhando no fim do treinamento.
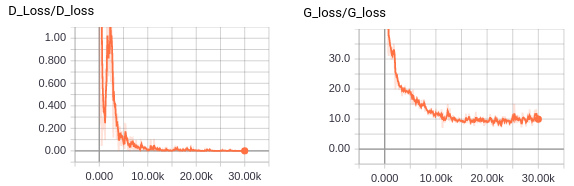
Aparentemente, nosso treinamento colapsou pois a rede descriminadora ficou muito boa. Isso pode ser visto pelo custo dela chegando próximo de zero. Um colapso era esperado, devido a simplicidade desta RAG. Eu ainda não posso torná-la estável pois não abordei as ferramentas necessárias para tal. Ainda assim, nas referências, colocarei uma palestra que fala sobre um truque extremamente simples para facilitar no treinamento de RAGs. Veja se você consegue estabilizar essa RAG sozinho (Dica: procure por One-sided label smoothing).
Referências
A maioria desse tutorial foi retirada do último capítulo do livro Deep Learning, por Goodfellow et al, 2016. Caso queira saber mais sobre RAGs, sugiro esta palestra do NIPS 2016, também por Ian Goodfellow. O notebook com toda a implementação da RAG aqui desenvolvida pode ser encontrado no meu GitHub.











