Posted on 30/07/2017

Aviso

Este é um tutorial mais avançado. O que não significa que ele seja mais difícil do que os outros, apenas que a minha série de tutoriais ainda não cobre todos os pré-requisitos para se entender o que colocarei aqui. Eventualmente, este tutorial se juntará à série.

Conteúdo

1. Introdução
2. Intuição
3. Formulação Matemática
4. Implementação
5. Resultados
6. Referências

Introdução

Nas palavras de Bengio e Goodfellow, “Máquinas de Boltzmann Restritas são o exemplo quintessencial de como modelos de grafos são utilizados em Deep Learning”. Elas tiveram um papel importantíssimo no ressurgimento das redes neurais em 2006, permitindo o treinamento eficiente de modelos profundos. Dentre as aplicações mais notáveis de MBR estão redução de dimensionalidade, pré-treinamento de redes neurais, detecção de fraudes e sistemas de recomendação colaborativos. Elas inclusive foram usadas pelos campeões do Prêmio Netflix, numa competição em que a empresa pagaria 1 milhão de dólares para quem conseguisse melhorar o seu sistema de recomendação em 10%.

Intuição

Máquinas de Boltzmann são modelos probabilísticos (ou geradores) não supervisionados, baseados em energia. Isso significa que elas associam uma energia para cada configuração das variáveis que se quer modelar. Intuitivamente, aprender nesses modelos corresponde a associar configurações mais prováveis aos estados de menor energia. Nesses estados existem unidades que chamamos visíveis, denotadas por \(v\), e unidades ocultas, denotadas por \(h\). Para tornar isso mais correto, pense na Máquina de Boltzmann abaixo como representando os possíveis estados de uma festa. Cada ponto branco corresponde a uma pessoa que conhecemos e cada ponto azul, a uma que não conhecemos. Esses pontos assumem valor 1 se a pessoa for festa e 0 caso ela faltar. A probabilidade de uma pessoa ir à festa depende da probabilidade de todas as outras pessoas irem à festa.

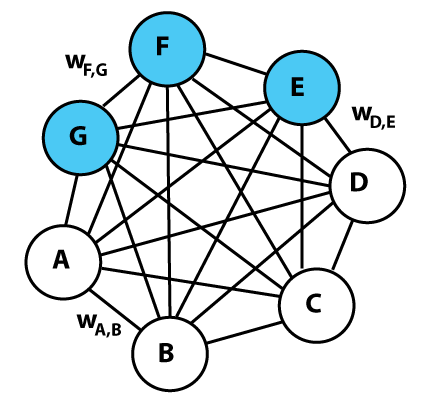
Podemos pensar nas conexões como a relação entre as pessoas. Assim, a probabilidade de uma pessoa ir à festa depende dessas conexões, mas apenas se contabiliza as conexões das pessoas presentes (i.e. com 1 no ponto). Por exemplo, digamos que a conexão entre \(v_1\) e \(v_4\) seja negativa, indicando que essas pessoas não se gostam. Assim, se uma delas for a festa, a probabilidade da outra ir diminui. Note que algumas conexões podem ter valor próximo de zero, indicando que as pessoas são indiferentes entre si. Nesse caso, a presença de uma pessoa na festa não influencia diretamente na probabilidade de presença da outra, mas ainda pode haver influência indireta, por meio de outras pessoas. Por fim, há um estado da festa em que a maioria das pessoas presentes não se gostam. Esse estado é de bastante tensão ou energia e há uma tendência para que ele não ocorra frequentemente. As Máquinas de Boltzmann capturam isso ao colocar pouca probabilidade em estados com muita energia.

Com esse exemplo você já deve ter percebido que Máquinas de Boltzmann são extremamente complicadas. Afinal, para saber a probabilidade de que uma unidade esteja ligada (seja 1), é preciso saber o estado de outras, já que podem haver relações indiretas. De fato, Máquinas de Boltzmann são tão complicadas que ainda não mostraram utilidade prática. Por isso teremos que restringi-las de alguma forma. As Máquinas de Boltzmann Restritas cumprem esse papel. Elas são Máquinas de Boltzmann com a condição de que não há conexões diretas entre as unidades visíveis nem entre as ocultas. Isso as torna mais simples e práticas, mas também menos intuitiva; nosso exemplo da festa deixa de fazer muito sentido quando apenas pessoas conhecidas só interagem diretamente com pessoas desconhecidas. Em vez disso, infelizmente, terei que fornecer uma explicação intuitiva mais abstrata.

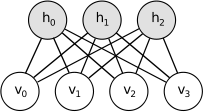
Apesar da restrição, Máquinas de Boltzmann Restritas, em teoria, conseguem representar qualquer fenômeno que quisermos, contanto que ela tenha unidades ocultas \(h\) suficiente. As unidades visíveis nesse caso são as variáveis cuja interação entre si queremos entender. Com as MBR, forçamos a relação entre as unidades visíveis a acontecer indiretamente, por meio das unidades ocultas. Assim, quanto mais unidades ocultas, maior a capacidade da MBR de capturar interações complexas entre as variáveis.

Formulação Matemática

Em termos estatísticos, MBR definem uma distribuição de probabilidade:

em que \(Z\) é o fator normalizador, também chamado de função de partição, \(\sum_{v,h} e^{-E(\pmb{v,h})}\). O custo para otimização então é simplesmente o negativo da \(\log\) probabilidade

Treinar esses modelos equivale a utilizar gradiente descendente estocástico na \(\log\) probabilidade empírica e maximizar a \(\log\) verossimilhança. Para as Máquinas de Boltzmann Restritas, a energia é dada por

em que \(\pmb{b}\) e \(\pmb{c}\) são termos de viés das camadas visíveis e ocultas, respectivamente. Note como a energia é linear nos parâmetros, o que nos dá derivadas simples e eficientes de computar. A restrição nas MBR diz respeito ao fato de não haver conexões entre as unidades ocultas nem entre as unidades visíveis. Como consequência, o estado das unidades ocultas é condicionalmente independente, dado o estado visível e o estado visível é condicionalmente independente, dado o estado oculto. Em termos mais intuitivos, se tivermos o estado oculto, podemos retirar amostrar do estado visível de maneira eficiente, já que não temos que nos preocupar como diferentes variáveis desse estado interagem entre si e vice-versa.

Aqui, veremos Máquinas de Boltzmann Restritas binárias. Isso significa que cada unidade estará ligada ou desligada e a probabilidade disso é dada pela ativação sigmoide de cada unidade, ou neurônio:

Com essa especificação binária, o gradiente da \(\log\) probabilidade assume uma forma particularmente interessante. Não é o propósito deste tutorial derivar esse gradiente, até porque vamos computar derivadas automaticamente, com autodiferenciação. Assim, vou apenas colocar o resultado final:

O primeiro termo dessa derivada é chamado de fase positiva, pois seu papel é aumentar a probabilidade dos dados. Você pode pensar nele como a média da derivada da energia quando amostras dos dados estão acopladas no lugar das unidades visíveis. O segundo termo é o que chamamos de fase negativa, pois seu papel é reduzir a probabilidade de amostrar geradas pelo modelo. Você pode pensar nele como a média da derivada da energia quando não há amostras acopladas no lugar das unidades visíveis. Para aqueles interessados, o desenvolvimento dessas derivadas podem ser conferido nestas notas de aula do curso Introduction to Neural Networks and Machine Learning (CSC321, 2014), da Universidade de Toronto.

Devido à independência condicional, o primeiro termo relativo à fase negativa pode ser computado diretamente, bastando para isso colocar amostras dos dados em \(\pmb{v}\) e computar a probabilidade de \(\pmb{h}\). O problema então é computar o temo negativo. Ele é simplesmente a esperança de todas as configurações possíveis dos dados \(\pmb{X}\) sob a distribuição do modelo! Como isso costuma ser maior que o número estimado de átomos no universo, precisaremos de algum corta caminho para computar o termo negativo.

Vamos aproximar essa esperança com MCMC (Cadeia de Markov Monte Carlo), isto é, vamos inicializar \(N\) Cadeias de Markov independentes nos dados e retirar iterativamente amostras de \(\pmb{h}\) e de \(\pmb{v}\). Esse processo iterativo recebe o nome de Amostragem de Gibbs alternada.

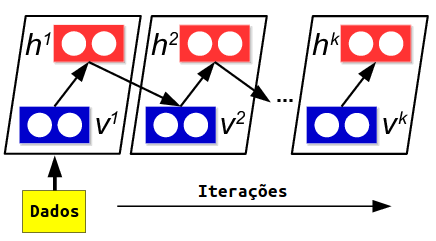
Matematicamente (abaixo, superscrito denota iteração, não exponente),
\(\pmb{v}_n^0 = \pmb{x}_n\)

Então substituimos a espeança pela média que a aproxima

Contrastive Divergence

Ainda precisamos resolver um problema, que é rodar a Cadeia de Markov infinitamente (ou por muito tempo) para conseguir a aproximação desejada. Uma observação bastante surpreendente é que, na prática, executar apenas uma amostragem de Gibbs alternada (i.e. uma iteração de MCMC) é suficiente para se conseguir uma aproximação boa o suficiente para o treino. Essa uma iteração é o que chamamos de Contrastive Divergence 1 ou CD1. Conforme o treinamento ocorre e queremos atualizações dos parâmetros mais refinadas, podemos aumentar o número de iteração e treinar a MBR com CD3. A forma mais comum de treinamento é começar com CD1, depois passar para CD3, então CD5 e, por fim, CD10.

Implementação

Vamos implementar uma Máquina de Boltzmann Restrita em TensorFlow. Ela será utilizada para modelar a distribuição de dados MNIST. O fato desses dados serem imagens nos permitirá mostrar alguns fenômenos fofos interessantes do aprendizado de MBRs, mas elas podem ser usadas em outros tipos de dados. Como esse é um modelo não supervisionado, só precisaremos das imagens e podemos descartar as classes.

import tensorflow as tf # para Deep Learning
import numpy as np # para computação numérica
from tensorflow.examples.tutorials.mnist import input_data # dados MNIST

data = input_data.read_data_sets("tmp/", one_hot=False)
data = np.random.permutation(data.train.images) # só precisamos das imagens aqui

Implementaremos a MBR como uma classe. Os hiper-parâmetros do modelo serão o número de unidades visíveis, de unidades ocultas e passos de CD. No método de inicialização da classe incluiremos o grafo TensorFlow, assim conseguiremos adicionar nós nele e executá-lo a partir de outros métodos. Já inicializaremos os pesos \(\pmb{W}\) e vieses das unidades observáveis e visíveis \(\pmb{b}\) e \(\pmb{c}\). Iremos também criar uma variável compartilhada para salvar os parâmetros \(\pmb{W}\) em formato Numpy, pois iremos visualizá-los no futuro e queremos acessá-los facilmente.

class RBM():
    def __init__(self, nv=28*28, nh=512, cd_steps=3):
        self.graph = tf.Graph() # define o grafo TensorFlow do modelo
        with self.graph.as_default(): # abre o grafo
            
            # define as variáveis do modelo
            self.W = tf.Variable(tf.truncated_normal((nv, nh)) * 0.01)
            self.bv = tf.Variable(tf.zeros((nv, 1))) 
            self.bh = tf.Variable(tf.zeros((nh, 1)))
            
            self.cd_steps = cd_steps # números de iterações de Contrastive Divergence
            self.modelW = None # para salvar os pesos do modelo em formato numpy

Agora, vamos definir dois métodos auxiliares. bernoulli gerará um vetor aleatório de 0s e 1s, segundo uma distribuição Bernoulli, a partir de um vetor de probabilidades p. É importante que os elementos de p estejam entre 0 e 1 para representarem probabilidades válidas. O método energy computará a energia média de um mini-lote de dados, segundo a fórmula de energia que vimos acima para as MBR.

    def bernoulli(self, p):
        '''Retira amostras Bernoulli segundo um vetor de probabilidades p.'''
        return tf.nn.relu(tf.sign(p - tf.random_uniform(p.shape)))
    
    def energy(self, v):
        '''Energia da MBR, dado um estado visível v.'''
        b_term = tf.matmul(v, self.bv)
        linear_tranform = tf.matmul(v, self.W) + tf.squeeze(self.bh)
        h_term = tf.reduce_sum(tf.log(tf.exp(linear_tranform) + 1), axis=1) 
        return tf.reduce_mean(-h_term -b_term)

Antes de definir o método que realizará as amostragens de Gibbs, vamos definir sample_h, para retirar amostras das unidades ocultas dadas as unidades visiveis, e sample_v, para retirar amostras das unidades visíveis, dadas as unidades ocultas. Em ambos os casos, realizamos transformações lineares nas quais multiplicamos as unidades pelos parâmetros \(\pmb{W}\) e adicionamos os vieses. Quando estamos propagando do estado visível para o oculto, a multiplicação ocorre normalmente, mas na propagação do estado oculto para o visível, devemos lembrar de transpor \(\pmb{W}\). Os métodos então retiram amostras Bernoulli dos estados ocultos e visíveis, convertendo a transformação linear em uma probabilidade com a função logística e, em seguida, retirando as amostras com o método bernoulli.

    def sample_h(self, v):
        '''Retira uma amostra do estado oculto h, dado o estado visível v'''
        ph_given_v = tf.sigmoid(tf.matmul(v, self.W) + tf.squeeze(self.bh))
        return self.bernoulli(ph_given_v)
    
    def sample_v(self, h):
        '''Retira uma amostra do estado visível v, dado o estado oculto h'''
        pv_given_h = tf.sigmoid(tf.matmul(h, tf.transpose(self.W)) + tf.squeeze(self.bv))
        return self.bernoulli(pv_given_h)

Agora começa a parte difícil. Vamos implementar Contrastive Divergence com o loop do TensorFlow, tf.while_loop, que não é nada intuitivo. Antes de prosseguir, recomendo fortemente que você veja a documentação oficial do loop. Tanto o corpo quando a condição de parada do loop devem ser funções que aceitam como parâmetros todas as variáveis do loop. Nesse caso, essas variáveis serão (1) um contador i para marcar a iteração atual, (2) um inteiro k que define a condição de continuação do loop \(i<=k\), (3) as unidades visíveis que a cada iteração do loop serão propagas para cima, para as unidades ocultas, e para baixo, novamente para as unidades visíveis, em uma sequência alternada de amostragem de Gibbs. Por conta dos requerimentos de tf.while_loop, o método que implementa essa iteração de amostragem Gibbs terá os três argumentos que definimos acima. Ele atualizará i adicionando um e atualizará o estado visível propagando-o para cima e para baixo na MBR, mas o inteiro k passará inalterado pela função.

    def gibbs_step(self, i, k, vk):
        '''Realiza uma amostragem de Gibbs alternada'''
        hk = self.sample_h(vk)
        vk = self.sample_v(hk)
        return i+1, k, vk

Finalmente, implementamos um método train para treinar a MBR. Ele começa concluindo o grafo TensorFlow, usando os métodos que criamos até agora. Em primeiro lugar, adicionamos ao grafo nós que inicializam o estado visível com amostras dos dados. Os dados são pixeis que variam de 0 a 1, mas o estado visível deve ser um tensor aleatório segundo uma distribuição Bernoulli. Assim, vamos tratas o valor dos pixeis como sendo probabilidades do pixel estar ligado (ser 1). Isso pode ser feito com tf.round(...), arredondando cada pixel para 0 ou 1. Após inicializar o estado visível na iteração 0 e o estado visível após k amostragens de Gibbs, entramos no loop que realiza essas amostragens. Note como a condição de parada é uma função que retorna um tensor boleno e que aceita como argumento as variáveis do loop. Os argumentos que não o contador i e o inteiro que define a parada k são passados por meio de *args. Note também como restinguimos o loop para não executar em paralelo e não definir o backward pass. O loop retorna todas as variáveis do loop no seu estado final. Só nos interessa o estado visível no momento k, isto é,vk, então descartaremos as outras variáveis. Após o loop, precisamos usar tf.stop_gradient(vk) para garantir que o TensorFlow, no momento de otimização, não realize backpropagation pelas amostragens de Gibbs. A definição do custo então a ser otimizado vem da \(\log\) verossimilhança tal como definida acima. Trata-se simplesmente da diferença entre as energias de v e vk. Finalizamos o grafo com a definição do otimizador e do inicializador de variáveis e então entramos na fase de execução do grafo.

    def train(self, X, lr=0.01, batch_size=64, epochs=5):
        with self.graph.as_default(): # abre o grafo TF do modelo
            tf_v = tf.placeholder(tf.float32, [batch_size, self.bv.shape[0]])
            v = tf.round(tf_v) # inicializa v
            vk = tf.identity(v) # inicializa vk

            # realiza k passos de amostragem de Gibbs
            i = tf.constant(0) # contador do loop
            _, _, vk = tf.while_loop(cond = lambda i, k, *args: i <= k,
                                      body = self.gibbs_step,
                                      loop_vars = [i, tf.constant(self.cd_steps), vk],
                                      parallel_iterations=1,
                                      back_prop=False)

            vk = tf.stop_gradient(vk) # para não fazer backprop pela amostragem Gibbs
            loss = self.energy(v) - self.energy(vk) # função custo da MBR
            optimizer = tf.train.AdamOptimizer(lr).minimize(loss)
            init = tf.global_variables_initializer()
        
        with tf.Session(graph=self.graph) as sess:
            init.run() # inicializa as variáveis do modelo
            for epoch in range(epochs): # treina por N épocas
                losses = []
                for i in range(0, len(X)-batch_size, batch_size):
                    x_batch = X[i:i+batch_size] # faz o mini-lote
                    l, _ = sess.run([loss, optimizer], feed_dict={tf_v: x_batch})
                    losses.append(l)
                # mostra o custo na época
                print('Custo na época %d: ' % epoch, np.mean(losses), end='\r')
            self.modelW = self.W.eval() # salva os W do modelo em formato numpy

Podemos agora criar uma instância da classe que define a Máquina de Boltzmann Restrita, treiná-la por quantas épocas quisermos e com a forma de Contrastive Divergence desejada. Nesse caso, vamos treinar com CD3, por 25 épocas. Na GPU, isso é bem rápido mas demora mais de meia hora na CPU (Intel i5, quad core). Se não for rodar na GPU, sugiro reduzir o número de épocas para algo como 10 ou 5, o que não impactará muito nos resultados.

rbm = RBM(cd_steps=3)
rbm.train(X=data, lr=0.001, epochs=25)

Para maior conveniência, o código está todo no meu GitHub.

Resultados

Uma forma da avaliar a RBM é visualmente, mostrando os parâmetros \(\pmb{W}\) como imagens. Se o treinamento for bem-sucedido, os pesos devem conter informações úteis para modelar os dígitos da base MNIST.

Acima, nem todos os pesos são facilmente interpretados. Note como os pesos destacados em vermelho contém linhas pretas em cima ou embaixo. Os pixeis pretos significam valores negativos em \(\pmb{w}\) e podem ser interpretados como um filtro que impede a passagem de informações. Essas linhas pretas, então, capturam a informações de que os dígitos não ultrapassam a altura das linhas Assim, a MBR coloca pouca probabilidade em estados visíveis com pixeis positivos em locais mais altos ou mais baixos que essas linhas. O filtro destacado em amarelo provavelmente é útil para detectar traços inclinados na direita, como o do “7”.

Uma outra forma de avaliar o treinamento de MBR é usar os parâmetros aprendidos para inicializar os parâmetros de uma rede neural e então ver se isso melhora na performance de generalização. Isso foi o que fizerem em 2006 para reascender o interesse em redes neurais, mas vamos deixar isso para outro tutorial.

Referências

Este tutorial é amplamente baseado no do deeplearning.net e é praticamente uma tradução de Thano para TensorFlow. Para um maior entendimento teórico sobre MBR, sugiro a parte 1 e a parte 2 da série de vídeos de Geoffrey Hinton sobre Máquinas de Boltzmann Restritas. Por fim, recomendo a parte 3 do livro Deep Learning, sobre as fronteiras de pesquisa em Deep Learning. O código deste tutorial está no meu GitHub.