Posted on 29/06/2018

Aviso

Este é um tutorial mais avançado. O que não significa que ele seja mais difícil do que os outros, apenas que a minha série de tutoriais ainda não cobre todos os pré-requisitos para se entender o que colocarei aqui. Eventualmente, este tutorial se juntará à série.

Conteúdo

1. Introdução
2. Variável de Confusão
3. Hipóteses para Inferência Causal
4. Ponderação Pelo Inverso da Probabilidade de Tratamento (IPTW)
5. Regressão Estrutural
6. Estimadores Duplamente Robustos
7. Implementação
8. Referências

Introdução

Em muitas situações uma simples previsão de um modelo de aprendizado de máquina não é suficiente e o que se quer mesmo é saber como uma variável influencia outra. Alguns exemplos são quando queremos entender quanto um remédio impacta na probabilidade de cura, um treinamento impacta na produtividade do trabalhador ou quanto o limite do cartão de crédito influencia no risco de um cliente. Infelizmente, modelos de prateleira de aprendizado de máquina são feitos para otimizar uma previsão explorando correlações, não causalidade.

Como um exemplo simples, considere o caso que apenas trabalhadores mais dedicados escolhem fazer um treinamento. Nesse caso o modelo de aprendizado de máquina vai entender que o treinamento está associado a alta produtividade, mesmo que o treinamento não tenha efeito nenhum. Nesse caso temos um viés positivo criado pelo fato de trabalhadores que já são mais produtivos escolherem fazer o treinamento (também chamado de viés de seleção). Também é possível casos de viés negativo que fazem com que o modelo aprenda uma relação aparentemente contraditória entre as variáveis. Como exemplo, considere o caso de cartão de crédito em que clientes com menor risco tendem a receber um limite maior, fazendo com que o modelo acredite que mais limite está associado a menos risco.

Vieses desse tipo são comuns em estudos observacionais - quando o cientista não controla o processo gerador de dados, mas apenas observa registros do que ocorreu. Métodos Duplamente Robustos são uma forma de mitigar esses vieses.

Variável de Confusão

O motivo que torna inferência causal tão complicada é variáveis de confusão. São variáveis que impactam tanto na variável resposta \(Y\) quanto no tratamento \(T\) que influencia essa variável resposta. Numa forma de diagrama (ou grafo) podemos visualizar variáveis de confusão da seguinte forma:

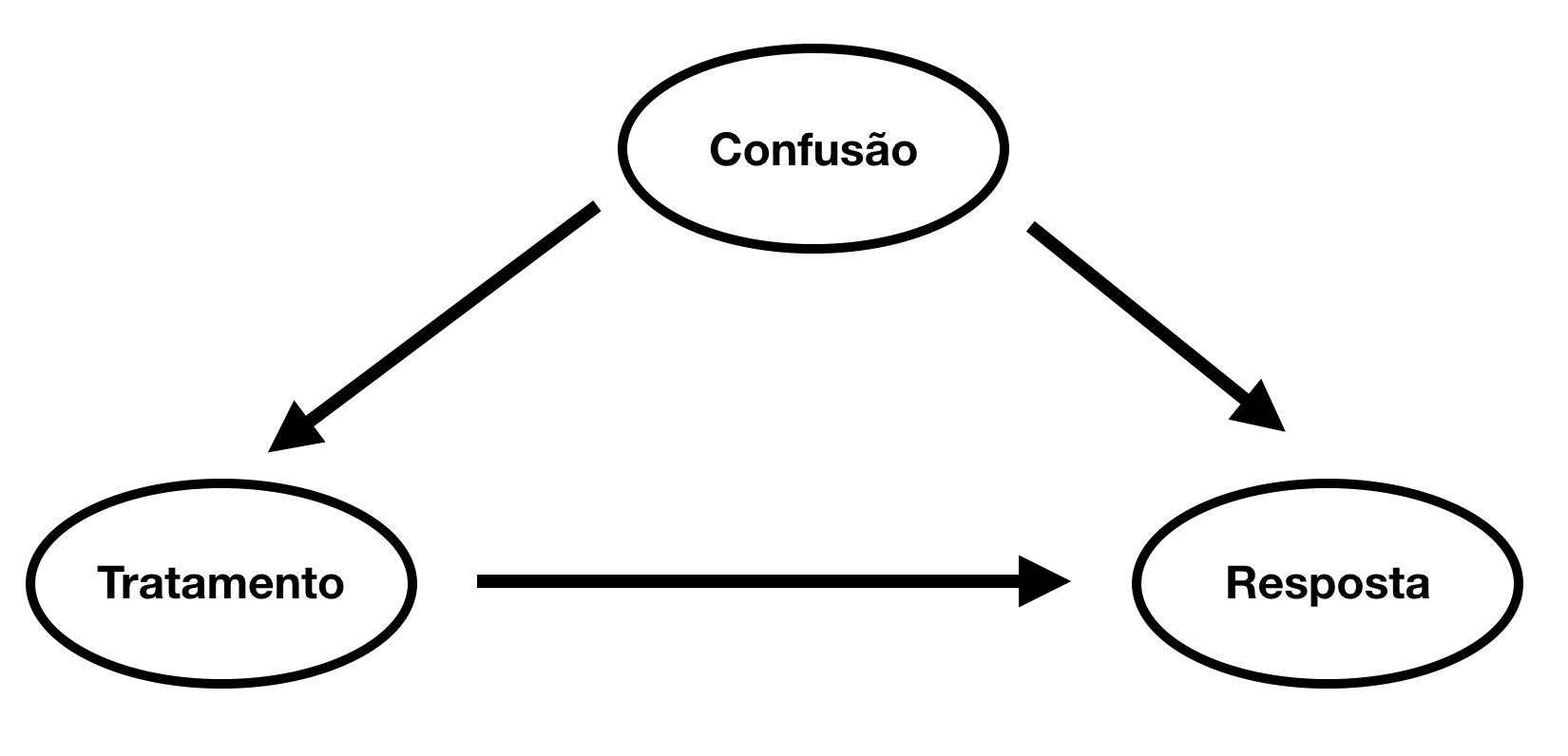
Trazendo isso para um dos nossos exemplos, a variável de confusão pode ser a aptidão de um funcionário ao seu trabalho (note que não precisa ser mensurável), algo que impacta tanto na sua produtividade quanto na sua probabilidade de escolher fazer o treinamento. Quando não levamos em conta as variáveis de confusão, o efeito de um tratamento será enviesado, já que algo a mais está contribuindo para a mudança na variável resposta.

Se soubermos como essas variáveis se correlacionam podemos até saber a direção do viés. Por exemplo, se a as correlações tiverem mesmo sinal, como no caso em que a variável de confusão \(C\) é positivamente correlacionada tanto com o tratamento \(T\) quanto com a resposta \(Y\), teremos um viés positivo, isto é, o efeito do tratamento aparentará ser mais forte do que de fato é. Esse é o caso do treinamento dos funcionários. Por outro lado, se as correlações tiverem sinais invertidos, como \(Corr(C, Y) > 0\) e \(Corr(T, Y) < 0\), o viés será negativo, isto é, o tratamento aparentará ter um efeito mais fraco ou até inverso ao real. Um exemplo desse caso é quando um medicamento \(T\) é dado de acordo com uma maior severidade \(C\) de uma doença. Isso faz parecer que o efeito do tratamento na quantidade de dias que o paciente passa internado \(Y\) é negativo.

Hipóteses para Inferência Causal

Um cenário ideal para inferência causal é quando podemos rodar um teste aleatório. Continuando no exemplo do treinamento, uma forma de conseguir isso selecionar aleatoriamente uma fração dos funcionários para realizá-lo e manter outra como controle. Ao final do experimento, poderíamos comparar a produtividade \(P\) dos trabalhadores que fizeram o treinamento (vamos chamá-los de \(P_1\)) com a dos que não fizeram, \(P_0\)

Em que \(avg\) é a média amostral de uma quantidade. Infelizmente nem sempre podemos - ou melhor, quase nunca - conduzir um teste aleatório. Isso porque eles ou são muito caros, ou não éticos (imagine forçar mães grávidas a fumar para achar o impacto do cigarro na gravidez) ou simplesmente difíceis de controlar. No caso do treinamento, por exemplo, mesmo que escolhamos aleatoriamente os participantes, não podemos forçar aqueles que escolhemos a participarem.

Por conta disso, teremos de nos virar com dados observacionais e tentar extrair deles o valor causal de uma variável. Porém, antes disso, precisamos saber o que é necessário para que isso seja ao menos possível.

Inferência causal só é possível diante de algumas hipóteses:

1. Unidade Estável de Tratamento. A primeira hipótese requer que as unidades observadas não influenciem o resultado do tratamento umas das outras.

2. Ingorabilidade ou Sem Variáveis de Confusão não Mensuradas. Essa hipótese diz que sabemos o valor de todas as variáveis que influenciam na designação do tratamento. Uma outra forma de dizer isso é que, dado o valor das variáveis que influenciam na designação do tratamento, essa designação é como se fosse aleatória. Formalmente, essa hipótese diz que dada as variáveis pré tratamento, a resposta potencial é independente da designação dos tratamentos, ou, matematicamente \( (Y^1, Y^0) ⫫ T \mid X\), em que \(Y^1\) é a resposta potencial dos tratados, isto é, o valor que a variável resposta teria se todos fossem tratados, e \(Y^0\) é a resposta potencial dos não tratados.

3. Positividade. A última hipótese requer que a designação do tratamento não seja determinística dada as variáveis pré tratamento. Em termos intuitivos, essa hipótese requer que todas as unidades tenham alguma chance de ter qualquer um dos tratamentos. Matematicamente, precisamos que \(P(A=a \mid X=x)>0 \ \forall \ x, a\)

Para nosso propósito aqui, as duas últimas hipóteses são as mais importantes. A primeira diz que se controlarmos fatores suficientes, mudanças na variável resposta será devido a um efeito causal; a segunda diz que é preciso haver alguma similaridade entre a população tratada e não tratada para podermos extrapolar o efeito de uma na outra.

Ponderação Pelo Inverso da Probabilidade de Tratamento (IPTW)

Tendo estabelecido as condições sob as quais inferência causal é possível podemos partir para o primeiro componente do nosso modelo de inferência causal, a ponderação pelo inverso da probabilidade de tratamento ou IPTW (Inverse Probability of Treatment Weighting). A intuição por trás dessa abordagem é bastante simples uma vez que tenhamos entendido bem o problema de inferência causal, então vamos recapitulá-lo.

Inferência causal é difícil pois a designação do tratamento não é aleatória e muitas vezes é influenciada por variáveis que também impactam na variável resposta (variáveis de confusão).

Uma boa ideia para resolver isso seria achar unidades bastante parecidas mas que receberam tratamentos diferentes. Mas o que seria nossa definição de parecido? Uma opção seria usar a distância euclidiana (produto interno), mas conforme o número de variáveis cresce isso se torna inviável devido a maldição da dimensionalidade. Uma segunda idea seira customizar nossa métrica de similaridade de acordo com o problema que queremos resolver, isto é, uma distância relativa as chances de receber o tratamento. Então, o que precisamos fazer é achar unidades não tratadas mas que tiveram grandes chances de serem tratadas e unidades tratadas que tiveram grandes chances de não serem tratadas. Esses dois tipos de unidades nos ajudarão a achar o efeito contrafactual do tratamento nos não tratados e do não tratamento nos tratados, isto é, o efeito contrário ao que ocorreu na realidade. Em termos mais práticos e diretos, o que essa ideia sugere é que devemos aumentar a influência (ponderar positivamente) dos raros casos de unidades que tiveram grandes chances de receber um tratamento mas não o receberam e vice versa para os que receberam.

OK. Supondo que temos essa propensão de tratamento \(\pi(x)\) que nos dá corretamente a probabilidade de uma unidade receber o tratamento. Podemos com isso estimar a média da resposta se todos recebessem o tratamento \(E(Y^1)\) da seguinte forma

Em que \(t\) é a variável tratamento que é zero para os não tratados. Assim, o termo acima usa \(t\) para selecionar os tratados, zerando os não tratados, e usa \(\pi\) para ponderar as observação. Trata-se assim de uma simples média ponderada dos tratados em que aqueles que tem baixa propensão a receberem o tratamento recebem um peso maior.

Podemos estimar \(E(Y^0)\) de forma análoga

Com essas duas quantidades temos uma forma de estimar o efeito causal médio \(E(Y^1) - E(Y^0)\). Resta ainda saber como obter \(\pi\). Felizmente não há muito segredo nisso. Precisamos apenas de um modelo de aprendizado de máquina de classificação que preveja a designação do tratamento. Em outras palavras, precisamos de um modelo que use \(X\) para prever \(T\).

Modelo Estrutural de Regressão

A propensão de tratamento (propensity score) é o primeiro componente do nosso estimador duplamente robusto. Vamos agora ao segundo componente. Digamos que tenhamos um modelo \(m^1\) que nos dá a média condicional de uma amostra dado \(x\), \(m_1(x)=E(Y \mid T=1, x)\). Com isso, uma outra forma de obter \(E(Y^1)\) seria

Intuitivamente, o que temos acima é uma média das unidades que receberam tratamento (\(ty\)), onde usam \(t\) para zerar quem não tiver recebido o tratamento; para esses últimos, como não observamos \(y^1\), vamos usar \(m_1(x)\) como estimativa desse valor. Em resumo, trata-se de uma média de \(y\) dos que foram tratados em que usamos estimativas quando não temos o tratamento da unidade. Se \(m_1\) for bem feito, essa estimativa é não enviesada.

Podemos estimar \(E(Y^0)\) de forma análoga

Estimadores Duplamente Robustos

Já que gastamos um certo tempo entendendo os componentes acima, juntá-los em um só estimador poderá ser entendido numa simples fórmula. Novamente, partindo do objetivo de estimar \(E(Y^0)\). Nesse caso, será mais fácil entender o estimador se trabalharmos diretamente com esperanças em vez de médias amostrais então substituirei o \(\sum_{i=1}^n\) por \(E\). Com isso, \(E(Y^0)\) fica

Esse estimador é duplamente robusto no sentido em que basta um dos componentes estar correto para que ele seja não enviesado. Para ver isso, considere primeiro o caso em que o propensity score está errado mas o modelo \(m^1\) está correto. Nessa situação, temos que \(E[t-\pi(x)]=0\), ou seja

Que é simplesmente o estimador do propensity score como vimos acima. Agora para ver o que aconteceria se o propensity score estiver errado e o modelo estive correto vamos apenas reescrever a fórmula do estimador

Nesse caso, se o modelo for corretamente especificado, \(E[y - m^1(x)] = 0\) e o estimador acima se resume a \(m^1(x)\) e independe do propensity score.

Implementação

Para demonstrar um modelo causal, é melhor trabalharmos com dados sintéticos. Isso porque na vida real não temos como saber o efeito causal real nem as previsões contrafactuais. O código que gera os dados não é nada complexo mas vou omiti-lo aqui para manter o tutorial mais curto. Caso queira, esse código pode ser encontrado no meu GitHub. Os dados seguirão um exemplo de um tratamento \(t\) que afeta o número de dias até a recuperação de um paciente hospitalizado.

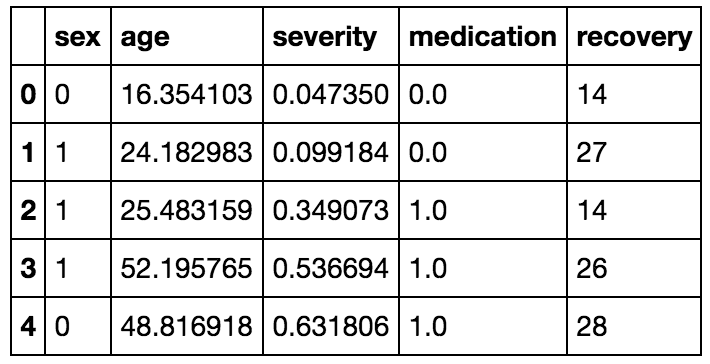
Eles foram gerados segundo o seguinte processo:

Note que Sexo e Severidade estão diretamente ligadas a probabilidade de tratamento enquanto Idade está indiretamente ligada, via influencia na severidade. Além disso, note que o parâmetro do tratamento é \(-1\). Assim, o efeito causal será de \(\exp(-1.0) \approx 0.37\), ou seja o tempo até a recuperação dos tratados é \(37\%\) do tempo de recuperação dos não tratados.

A nossa função geradora de dados retorna 3 sets: o primeiro tem a designação do tratamento aleatória, isto é, ignorando o processo descrito acima; o segundo são dados gerados exatamente como descrito acima; o terceiro são dados contrafactuais, isto é, com o tratamento trocado e o efeito de recuperação recalculado nessa população contrafactural. Note que, no mundo real, só teríamos o segundo set e, caso rodássemos um experimento aleatório, também teríamos o primeiro, mas os dados contrafactuais são impossíveis de se obter.

true_efect = np.exp(-1.0) # armazena o efeito causal
df_rnd, df_obs, df_ctf = make_confounded_data(50000) 
_, test_obs, _ = make_confounded_data(10000) # set de teste observacional

Também vamos gerar um set de teste para avaliar nossos modelo e garantir que não estão sobre ajustadno. Ná prática, isso seria obtido com um split aleatório dos dados. Vamos também importar algumas bibliotecas e ver a correlação entre as variáveis.

import pandas as pd # para manipulação de tabelas
import numpy as np # para computação numérica
import seaborn as sns # para gráficos
from matplotlib import pyplot as plt # para gráficos

# definimos algumas constantes
var_x = ["sex", "age", "severity"]
var_t = ["medication"]
resp_y = "recovery"

sns.heatmap(df_rnd.corr())
plt.show()

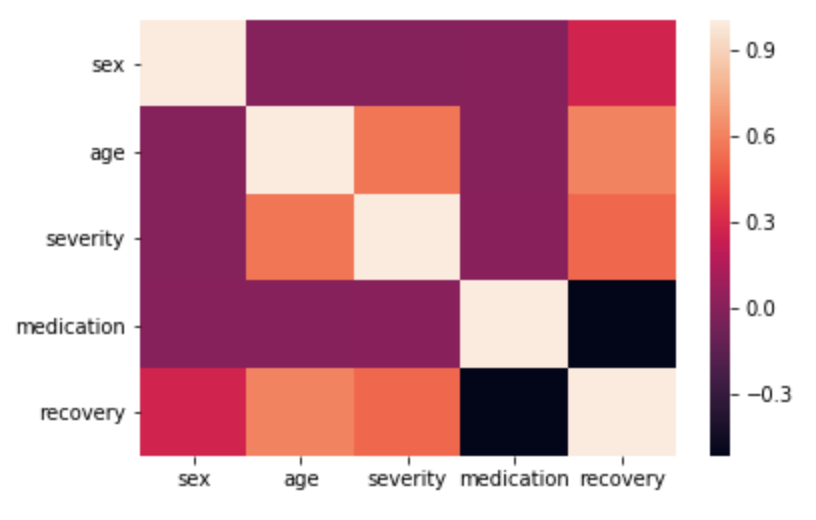
Como é de se esperar, no set aleatório não há correlação entre o medicamento e nenhuma outra variável de confusão. Além disso, o medicamente tem o que parece ser um efeito de \(-0.3\) nos dias até a recuperação. Quando olhamos as correlações dos dados observacionais a coisa muda de figura

sns.heatmap(df_obs.corr())
plt.show()

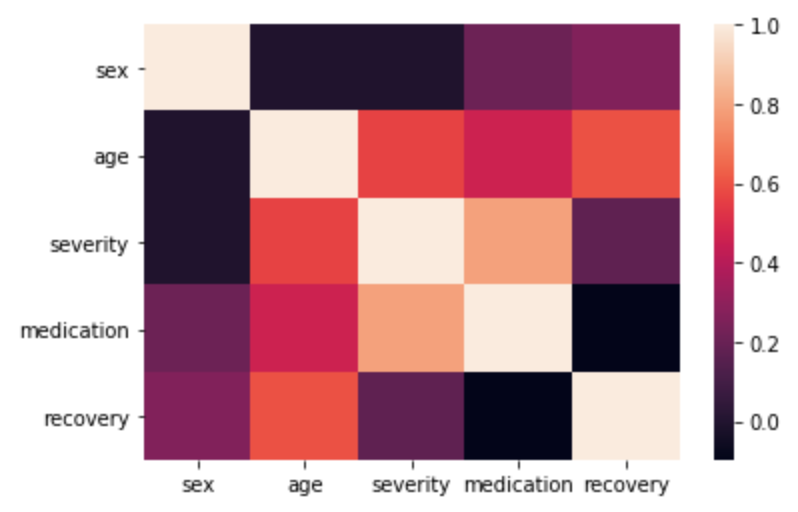
Agora vemos que o medicamento está correlacionado com todas as variáveis de confusão e parece ter correlação zero com a recuperação. Isso acontece pois o tratamento é positivamente correlacionado com a severidade, isto é, quanto maior a severidade maior a probabilidade de receber o tratamento. Assim, estamos diante de um caso de viés negativo, onde essa correlação faz parecer que o tratamento não tem efeito.

Para efeito de comparação, vamos ver o que aconteceria se não tratássemos esse problema com o cuidado exigido por um problema de inferência causal. Vamos pegar um modelo qualquer e usar as variáveis de confusão mais o tratamento para prever a recuperação. Nesse caso vou escolher florestas aleatórias mas tudo que será feito abaixo pode ser feito com qualquer modelo de aprendizado de máquina.

Modelo Sem Consideração Causal

from sklearn.ensemble import RandomForestRegressor

regr = RandomForestRegressor(n_estimators=100, max_depth=4, min_samples_leaf=100)
regr.fit(df_obs[var_x + var_t], df_obs[resp_y])

print("Train Score: ", regr.score(df_obs[var_x + var_t], df_obs[resp_y]))
print("Test Score: ", regr.score(test_obs[var_x + var_t], test_obs[resp_y]))

Train Score:  0.6842113937428888
Test Score:  0.6756330521689281

O modelo está bem ajustado. Agora vamos utilizá-lo para inferir o efeito causal médio. Para isso, primeiro criamos duas cópias dos dados observacionais, uma em que todos recebem o tratamento e outra em que ninguém o recebe. Para achar o efeito causal de cada unidade, vamos dividir a previsão no caso de tratamento pela previsão da mesma unidade no caso de não tratamento. Por fim, tiramos a média disso.

X_neg = df_obs.copy()
X_pos = df_obs.copy()

X_neg["medication"] = 0
X_pos["medication"] = 1

preds = regr.predict(X_pos[var_x + var_t]) / regr.predict(X_neg[var_x + var_t])
print("Efeito Causal Previsto:, ", preds.mean())

Efeito Causal Previsto:,  0.6286014281347522

Como podemos ver, sem considerar o viés, nosso modelo ingênuo de aprendizado de máquina acha que o tempo até a recuperação dos tratados é \(63\%\) dos tempo de recuperação dos não tratados, o que é um efeito menor do que os \(37\%\) real.

ax = sns.distplot(preds)
plt.axvline(np.mean(preds), label='Previsto', lw=5)
plt.axvline(true_efect, color='r', label='Real')
ax.set_xlabel('Efeito Causal')
plt.legend()
plt.show()

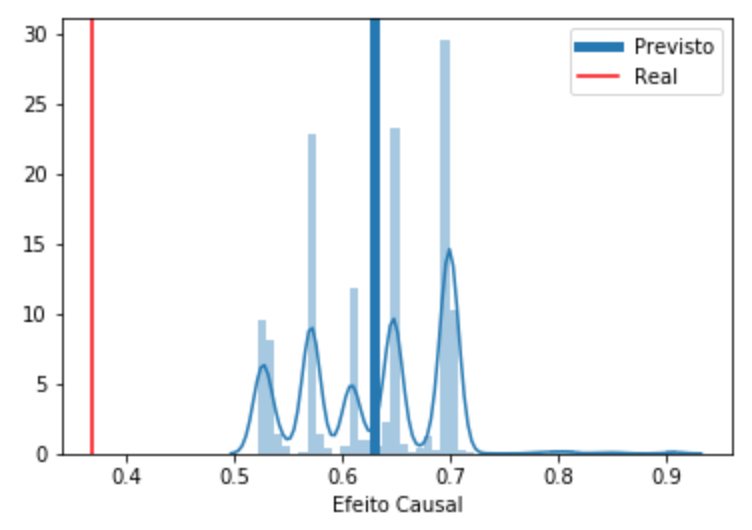
Podemos ver também como se sai nosso modelo na tarefa de prever os dados contrafactuais.

print("Score Contrafactual: ", regr.score(df_ctf[var_x + var_t], df_ctf[resp_y]))

Score Contrafactual:  0.5286251438622127

Apenas a título de curiosidade, podemos refazer a mesma análise mas agora nos dados em que o tratamento é aleatório.

regr = RandomForestRegressor(n_estimators=100, max_depth=4, min_samples_leaf=100)
regr.fit(df_rnd[var_x + var_t], df_rnd[resp_y])

X_neg = df_obs.copy()
X_pos = df_obs.copy()

X_neg["medication"] = 0
X_pos["medication"] = 1

preds = regr.predict(X_pos[var_x + var_t]) / regr.predict(X_neg[var_x + var_t])
print("Efeito Causal Previsto:, ", preds.mean())

Efeito Causal Previsto:,  0.37125007321366865

Desta vez o efeito causal é encontrado com sucesso.

Modelo Causal

Para simplificar a implementação, vamos fazer \(m^1\) e \(m^2\) em um só modelo \(m\). Vamos usar florestas aleatórias para ambos os modelos, \(m\) e o modelo de propensity. Note que embora a floresta aleatória do sklearn tenha um método .predict_proba essa não é de fato uma probabilidade real e deve ser calibrada. Isso é feito ajustando uma regressão logística em cima da previsão da floresta aleatória. Felizmente, o sklearn já tem um calibrador pronto então vamos simplesmente usá-lo.

from sklearn.ensemble import RandomForestClassifier # importa o modelo
from sklearn.calibration import CalibratedClassifierCV # importa o calibrador

# cria o modelo de propensity score
ps_model = CalibratedClassifierCV(RandomForestClassifier(n_estimators=100, max_depth=4, min_samples_leaf=100))
ps_model.fit(df_obs[var_x], df_obs[var_t].squeeze()) # ajusta o modelo

print("Train Score: ", ps_model.score(df_obs[var_x], df_obs[var_t].squeeze()))
print("Train Score: ", ps_model.score(test_obs[var_x], test_obs[var_t].squeeze()))

Train Score:  0.9215
Train Score:  0.9254

A performance de treino e teste é similar então podemos concluir que o modelo está bem calibrado. Além disso, o fato da performance do modelo não ser perfeita é um indício de que a terceira hipótese para inferência causal não é violada. Se pudéssemos prever perfeitamente o tratamento não poderíamos dizer que ele não seja determinístico dada as variáveis pré tratamento. A terceira hipótese também requer que todas as unidades tenham probabilidade não nula serem tratadas. Em outras palavras, é preciso que haja alguma sobreposição entre a população tratada e não tratada no que se refere ao propensity score. Podemos checar isso traçando um histograma do propensity score para os tratados e não tratado.

# cria um DataFrame com duas colunas. Uma com a probabilidade de tratamento P e outra com (1-P)
ps_score = pd.DataFrame(ps_model.predict_proba(df_obs[var_x]))

# adiciona aos nossos dados df_obs a primeira coluna (P) do DataFrame acima
ps_data = df_obs.assign(propensity_score = ps_score[0]) 

# plota a sobreposicão de populacoes
ax = sns.distplot(ps_data.query("medication==1.0")["propensity_score"], label="tratados")
sns.distplot(ps_data.query("medication==0.0")["propensity_score"], label="não tratados")
ax.set_xlabel('propensity socore')
plt.legend()
plt.show()

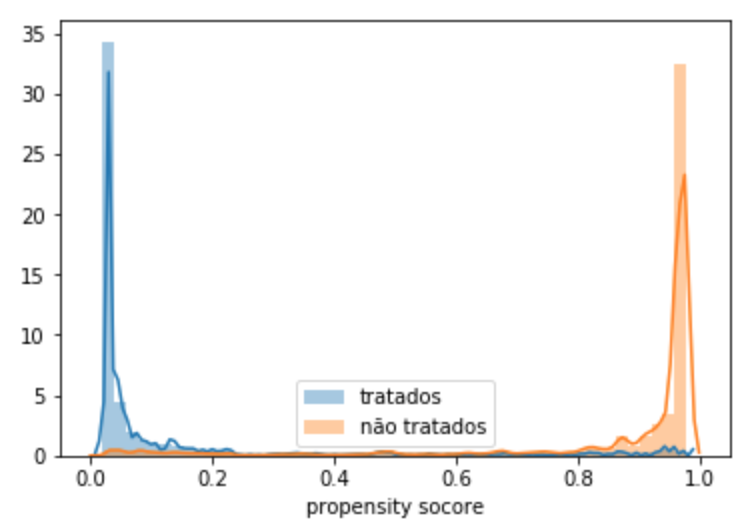
O gráfico acima mostra que, se a terceira hipótese de positividade não é violada, há muito pouca sobreposição nas populações tratadas e não tratadas. Isso tornará o problema de achar o efeito causal muito mais difícil.

Continuando com o nosso modelo duplamente robusto, precisamos agora ponderar os dados pelo inverso do propensity score. Para isso vamos usar o método .lookup do DataFrame. Ele aceita dois arrays do mesmo tamanho que o número de linhas que o DataFrame. O primeiro contém os indicies das linhas e o segundo o indicies das colunas que se quer. Nesse segundo, vamos passar a coluna de tratamento. Assim, quando este for 1 (tratado), dividiremos pela probabilidade de tratamento e quando for 0 (não tratado) dividiremos pela probabilidade de não tratamento

weight_data = df_obs.assign(weight = 1. / ps_score.lookup(np.arange(ps_score.shape[0]),
                                                          df_obs[var_t].astype(int).values.squeeze()))

Resta agora apenas ajustar \(m\) aos dados ponderados. Isso pode ser feito usando o parâmetro sample_weight da floresta aleatória.

struc_model = RandomForestRegressor(n_estimators=100, max_depth=7, min_samples_leaf=10)
struc_model.fit(weight_data[var_x + var_t],
                weight_data[resp_y].squeeze(),
                sample_weight=weight_data["weight"]) # passa a ponderação

print("Train Score: ", struc_model.score(weight_data[var_x + var_t], weight_data[resp_y].squeeze()))
print("Train Score: ", struc_model.score(test_obs[var_x + var_t], test_obs[resp_y].squeeze()))

Train Score:  0.8404561549023044
Train Score:  0.8313566196829696

O efeito causal pode ser obtido da mesma forma que haviamos feito antes.

X_neg = df_obs.copy()
X_pos = df_obs.copy()

X_neg["medication"] = 0
X_pos["medication"] = 1

preds = struc_model.predict(X_pos[var_x + var_t]) / struc_model.predict(X_neg[var_x + var_t])
print("Efeito Causal Previsto:, ", preds.mean())

Efeito Causal Previsto:,  0.428171125385169

Bem… Ainda não são os 37% que queríamos mas já é algo bem mais próximo do que os 62% obtido com um modelo sem considerações causais. Além disso, se olharmos a distribuição das previsões podemos ver que, embora a média esteja um pouco enviesada ainda, a moda da distribuição é quase exatamente o efeito causal real.

ax = sns.distplot(preds)
plt.axvline(np.mean(preds), label='Previsto', lw=5)
plt.axvline(true_efect, color='r', label='Real')
ax.set_xlabel('Efeito Causal')
plt.legend()
plt.show()

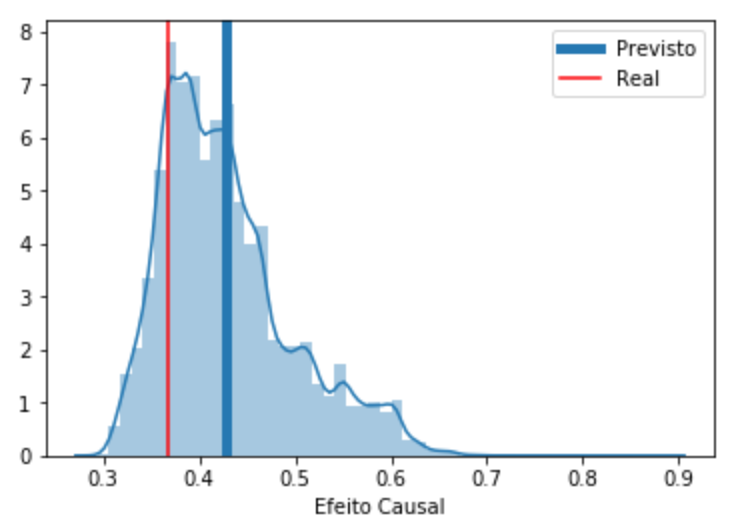
print("Score Contrafactual: ", struc_model.score(df_ctf[var_x + var_t], df_ctf[resp_y]))

Score Contrafactual:  0.8046587777963254

Podemos ver também que a performance desse modelo nos dados contrafactuais é bem melhor do que a do modelo ingênuo (0.528). Isso mostra que desenviesar os dados melhora o modelo para o caso contrafactual. Note que esses dados não estarão disponíveis na vida real então não se deve se ater a métricas de previsão quando ser for avaliar ou comparar modelos de inferência causal!

Referências

A parte da implementação e código é fortemente inspirado no post Causal Inference and Propensity Score Methods de Florian Wilhelm. A parte teórica foi tirada do curso A Crash Course in Causality: Inferring Causal Effects from Observational Data, da Universidade da Pennsylvania. Como sempre, todo o código e mais um pouco está disponível no meu GitHub.