Posted on 4/03/2017

Pré-requisitos

Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.

Conteúdo

• Introdução
• Justificativa matemática
• Implementação
• Indo um pouco além
• Considerações Finais

Introdução

Podemos entender regressão logística como o análogo de regressão linear para problemas de classificação. Esse tipo de problema surge quando queremos categorizar alguma variável por classes. Quando isso acontece, a variável \( \pmb{y} \) que queremos prever é discreta. Um exemplo seria saber se uma pessoa ganha mais de R \) 50000 anuais, com base nas suas informações socioeconômicas, ou saber se uma pessoa pedindo empréstimo vai pagar corretamente o que deverá.

Como exemplo ilustrativo, vamos supor que somos uma agência de seguros e estamos decidindo se devemos ou não segurar um carro, com base nas informações sociais dos seus donos. Por motivos de simplicidade, vamos dizer que a probabilidade da pessoa bater o carro só dependa do tempo que ela gastou na autoescola; nós temos acesso a esse tempo, mas não sabemos exatamente como ele se relaciona com a probabilidade da pessoa segurada sofrer um acidente automobilístico.

Nós então olhamos no nosso arquivo os casos de 15 pessoas, onde temos tanto os dados de tempo na autoescola e se elas sofreram ou não acidente. Se colocarmos nossos dados em um gráfico (x, y) ele seria mais ou menos da seguinte forma:

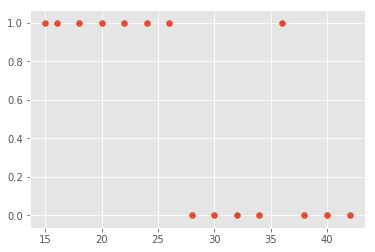
No eixo y, temos marcado com 1 se a pessoa sofreu um acidente e 0 caso contrário. No eixo x, temos o tempo que ela passou na autoescola. Nós podemos ver então que a maioria das pessoas que sofreram um acidente de carro passou pouco tempo na autoescola. Mas queremos mais do que isso. Queremos algum modelo capaz de prever a probabilidade da pessoa sofrer um acidente com base no tempo que durou a autoescola dela.

Uma forma ingênua de resolver esse problema é utilizar regressão linear. Como regressão linear produz como previsão um valor contínuo, nós podemos estabelecer algum limiar para as previsões. Vamos supor que fixemos esse limiar em 0,5: pessoas cuja previsão de acidente for maior do que isso serão consideradas de alto risco e não seriam seguradas (ou o seriam a um preço maior). A nossa esperança é que regressão linear produza como previsão a probabilidade da pessoa sofrer acidente, dado o tempo dela na autoescola (e nós veremos que isso não será o caso). A nossa linha de melhor ajuste então seria assim:

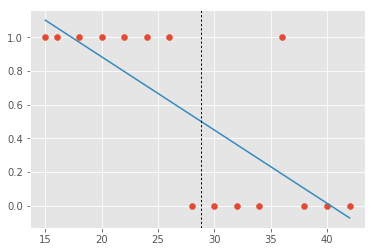
Nesse caso, utilizar regressão linear e estabelecer um limiar funcionaria muito bem! Se colocássemos o nosso limiar em 0.5, preveríamos que todos à direita da curva pontilhada não sofreriam um acidente e erraríamos em apenas dois casos! No entanto, suponha agora que nos nossos dados haja uma pessoa com muitas horas de autoescola. Digamos, umas 100 horas. Essa pessoa não sofreu nenhum acidente e de certa forma ter ela nos dados não traz muita informação nova: ela foi tão treinada que dificilmente preveríamos que sofreria um acidente. Em outras palavras, essa observação não gera incerteza O ideal seria então que o nosso algoritmo de previsão não desse muita atenção a essa pessoa e se concentrasse mais nas regiões de fronteira, onde é realmente difícil saber se a pessoa é de baixo ou alto risco. Infelizmente isso não acontece com regressão linear:

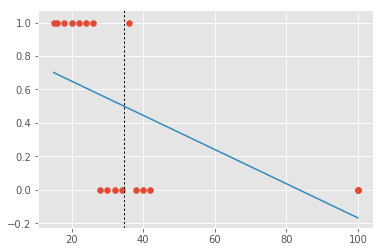
A presença dessa pessoa super treinada faz com que nossa linha de regressão seja puxada para a direita. Como consequência, iremos classificar muitas das pessoas de baixo risco como tendo alta probabilidade de sofrer acidentes. Podemos ver mais um comportamento estranho com o algoritmo de regressão linear: para pessoas com mais de 70 horas de autoescola, ele está prevendo uma probabilidade negativa de acidente, o que simplesmente não tem sentido.

Para resolver esses problemas, em vez de utilizar regressão linear, vamos utilizar a regressão logística sempre que nos depararmos com problemas de classificação. Regressão logística nos fornecerá uma previsão sempre entre 0 e 1, de forma que possamos interpretar seus resultados como uma probabilidade válida. Além disso, regressão logística não será influenciada por outliers que não fornecem muita informação nova, pois a atenção do algoritmo será concentrada na região de fronteira.

A intuição por trás de regressão logística é bastante simples: em vez de acharmos a reta que melhor se ajusta aos dados, vamos achar uma curva em formato de 'S' que melhor se ajusta aos dados:

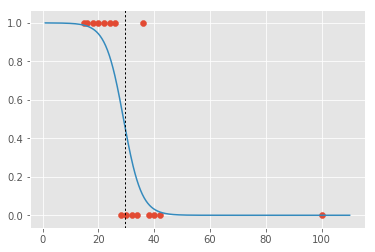
Justificativa matemática

Para implementar regressão logística, precisamos de apenas duas modificações ao algoritmo de regressão linear. Em primeiro lugar, precisamos utilizar uma função achatamento após a transformação linear, de forma que o valor previsto pelo modelo possa ser interpretado como uma probabilidade (lembre-se de que estamos tentando modelar uma variável binária, então queremos saber a probabilidade dela ser 0 ou 1). A função de achatamento que vamos utilizar é a função logística, ou sigmóide:

O gráfico dessa função tem o seguinte formato:

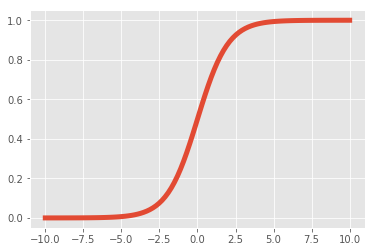
O que a função sigmóide faz é simplesmente converter o escore produzido pela transformação linear \( \pmb{X}\pmb{\hat{w}} \) em uma probabilidade, de forma que quanto maior o score, maior a probabilidade prevista e vice-versa. Podemos então utilizar 0.5 como um limiar, da mesma forma que havíamos feito com a nossa solução ingênua. A vantagem é que agora, além da previsão ser uma probabilidade válida, a regressão logística não será sensível aos pontos com escores muito altos ou muito baixos, onde a incerteza quanto a classificação é baixa.

Lembre-se de como com regressão linear tínhamos um modelo na forma \( \pmb{y}=\pmb{X}\pmb{w} + \pmb{\epsilon} \), de forma que nossas previsões eram da forma \( \pmb{\hat{y}}=\pmb{X}\pmb{\hat{w}} \). Agora, com regressão logística, nosso modelo fica:

De forma que nossas previsões serão uma probabilidade, resultado de \( \pmb{\hat{y}}=\sigma(\pmb{X}\pmb{\hat{w}}) \). Novamente, nosso objetivo será aprender os parâmetros \( \pmb{\hat{w}} \) de forma a minimizar uma função custo. O que nos leva a segunda modificação que devemos fazer ao algoritmo de regressão linear.

Por motivos de otimização e estatísticos, não seria razoável utilizar a função custo de distância quadrada entre o valor observado e previsto. Infelizmente a explicação detalhado do porque disso envolve muita matemática que acabaria desviando do propósito desse tutorial. Por isso, vou pedir que simplesmente acreditem em mim que, para problemas de classificação, existe uma função custo melhor. No final da página, referenciarei fontes que detalham isso. Assim, em vez de tentarmos minimizar a distância quadrada entre o valor previsto e o observado, nós vamos minimizar a entropia cruzada:

Para entender essa função custo, vamos analisar cada caso separadamente. Se \( y=1 \) e \( \hat{y}=1 \), \( -log(\hat{y})=0 \). No entanto, quanto mais \( \hat{y} \) se aproxima de 0, \( -log(\hat{y}) \) cresce exponencialmente para o infinito. Por outro lado, se \( y=0 \) e \( \hat{y}=0 \), podemos ver que \( -log(1-\hat{y})=0 \). Mas \( -log(1-\hat{y})=0 \) vai para o infinito conforme \( \hat{y} \) se distancia de \( 0 \). Podemos resumir a função custo de entropia cruzada da seguinte forma:

Podemos então substituir \( \hat{y} \) por \( \sigma(\pmb{X}\pmb{w}) \) e diferenciar \( L \) com respeito aos parâmetros:

Como é bastante entediante e desnecessário realizar os próximos passos dessa diferenciação, vamos pular direto par o resultado, que é incrivelmente simples:

Com isso, já temos toda a informação necessária para implementar uma regressão logística: bastará atualizar os parâmetros \( \pmb{\hat{w}} \) iterativamente com gradiente descendente.

Implementação

Nossa implementação de regressão logística será extremamente similar a de regressão linear com gradiente descendente. A única modificação será na atualização do gradiente, que utilizara as derivadas computadas acima, e na previsão, que será agora um valor binário:

class logistic_regr(object):

    def __init__(self, learning_rate=0.0001, training_iters=100):
        self.learning_rate = learning_rate # taxa de aprendizado
        self.training_iters = training_iters # iterações de treino
        
    
    def _logistic(self, X):
        '''Função logística'''
        return  1 / (1 + np.exp(-np.dot(X, self.w_hat)))
    
    
    def fit(self, X_train, y_train):
        
        # formata os dados
        X = X_train.reshape(-1,1) if len(X_train.shape) < 2 else X_train
        X = np.insert(X, 0, 1, 1)
               
        # inicia os parâmetros com pequenos valores aleatórios (nosso chute razoável)
        self.w_hat = np.random.normal(0,1, size = X[0].shape)
        
        # loop de treinamento
        for _ in range(self.training_iters):
            
            gradient = np.zeros(self.w_hat.shape) # inicia o gradiente
            
            # atualiza o gradiente com informação de todos os pontos
            for var in range(len(gradient)):
                gradient[var] += np.dot((self._logistic(X) - y_train), X[:,var])
            
            gradient *= self.learning_rate # multiplica o gradiente pela taxa de aprendizado

            # atualiza os parâmetros
            self.w_hat -= gradient
            
            
    def predict(self, X_test):
        
        # formata os dados
        if len(X_test.shape) < 2:
            X = X_test.reshape(-1,1)
        X = np.insert(X, 0, 1, 1)
        
        # aplica função logística
        logit = self._logistic(X) 
        
        # aplica limiar
        return np.greater_equal(logit, 0.5).astype(int)

E pronto! Temos nossa própria implementação de regressão logística! Contudo, é preciso chamar atenção para alguns detalhes. Embora a implementação acima produza resultados extremamente próximos aos obtidos com uma regressão logística de mercado, eu precisei rodar muitas iterações de treino para isso. Na prática, então, não é recomendado utilizar a implementação acima.

Não sei exatamente como é a implementação da regressão logística que usei como comparação, mas sei que há diversas formas de acelerar o treinamento da nossa. Particularmente, qualquer melhoria da otimização por gradiente descendente funcionaria para acelerar o treinamento. Como eu já explorei isso em outro tutorial, não falarei dessas melhorias aqui. Ainda mais, na prática, basta utilizar um algoritmo de regressão logística já pronto que não precisaremos nos preocupar com esses detalhes de otimização.

Você pode conferir essa implementação no meu GitHub.

Indo um pouco além: Perceptrons e a inspiração biológica para regressão logística

Regressão logística pode ser vista como um tipo de perceptron, um algoritmo antigo de inteligência artificial que se inspira livremente no funcionamento dos neurônios.

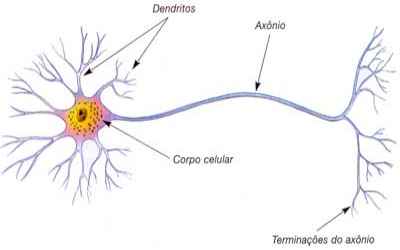
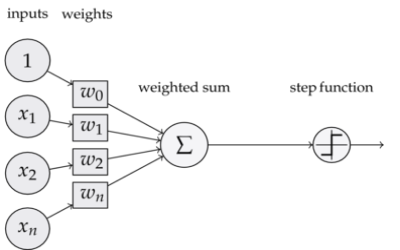
De maneira bem simplificada, podemos pensar nos neurônios como células que recebem sinais pelos seus dendritos, processam esse sinal e ativam caso o sinal processado exceda algum limiar. Isso é exatamente o que a regressão logística faz: ela pondera o sinal das múltiplas variáveis, soma esses sinais e passa-os por uma função achatamento, produzindo uma probabilidade. Se essa probabilidade for maior do que um limiar, a regressão logística dispara, ou seja, retorna 1. Caso os sinais recebidos não forem fortes o suficiente, a regressão logística não dispara, produzindo zero. As diferenças entre perceptrons e regressão logística são tão sutis que nem vale a pena mencioná-las. Mais importante é saber do que são capazes esses modelos e quais as suas limitações.

Particularmente, precisamos entender que a regressão logística e os perceptrons acham uma linha de separação entre as classes. Se essa linha existir, esses modelos irão encontrá-las com certeza, dado uma taxa de aprendizado suficientemente baixa e um número suficientemente alto de iterações de treino:

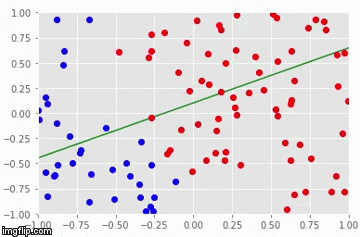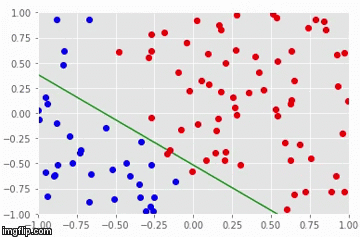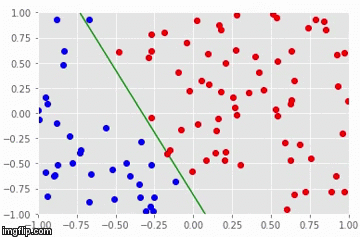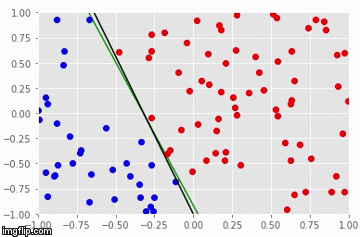
Quanto às limitações, existem duas que merecem destaque. A primeira é que nem regressão logística e nem perceptrons conseguem achar a fronteira de separação entre as classes se essa fronteira não for uma reta. Essa limitação vem do fato desses modelos serem lineares. A segunda limitação é que regressão logística e perceptrons acham apenas alguma reta de separação entre as classes, mas não é garantido que eles encontrem a melhor reta de separação. Como exemplo, veja a imagem a seguir:

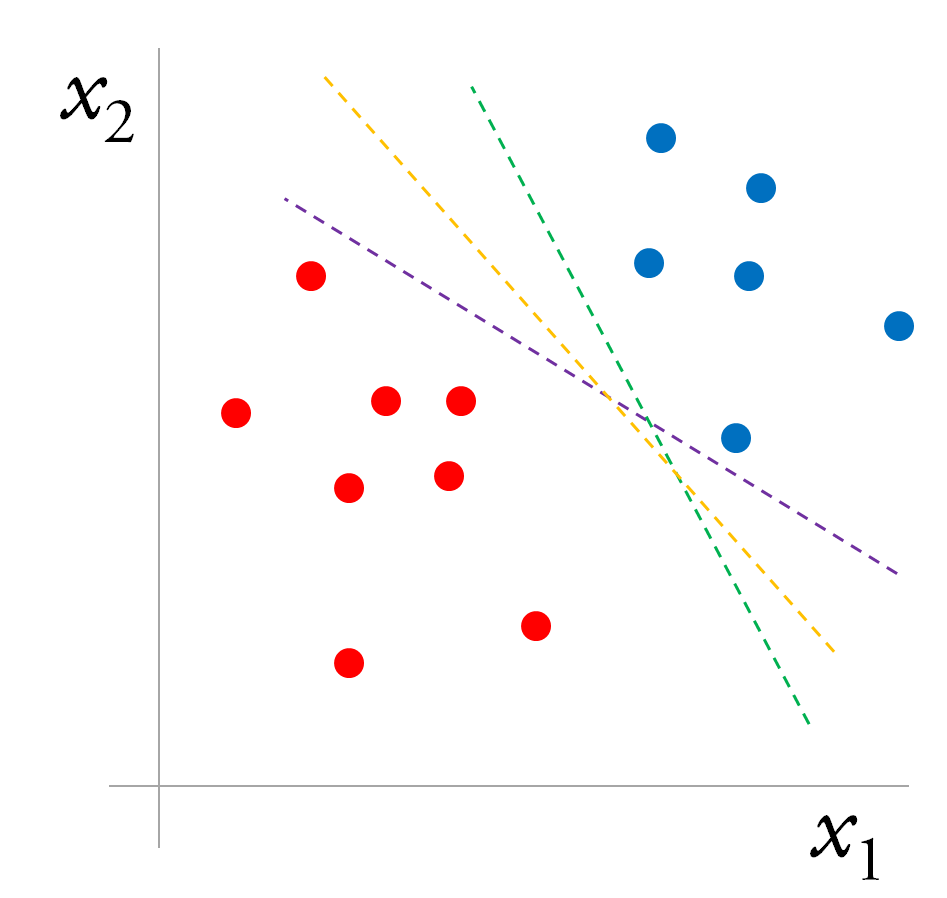
Temos duas classes, azul e vermelha, que gostaríamos de separar. Isso pode ser feito por qualquer uma das linhas abaixo. Nossa intuição diz que a linha amarela é a melhor dentre as três, mas nada garante que a regressão logística ou o perceptron encontrarão a melhor linha separadora. Na verdade, é muito mais provável que eles encontrem uma linha não ótima, pois o treinamento normalmente é interrompido quando todos os exemplos do set de treino são classificados corretamente. Para achar a melhor linha, precisaremos de um outro algoritmo: as máquinas de suporte vetorial.

Considerações Finais

Regressão logística é de longe o algoritmo de classificação mais conhecido e mais utilizado. Assim como no caso de regressão linear, regressão logística já te levará bem longe em termos de acurácia, mesmo sendo extremamente simples. Além disso, regressão logística é o bloco fundamental com o qual são construídas as redes neurais artificias. Por esse motivo, é extremamente importante entender bem esse modelo de classificação. Caso o meu tutorial não tenha ficado claro, seguem algumas referências externas que abordam o assunto de forma muito mais detalhada:

• Esta série de vídeos da Universidade de Stanford;
• Esta série de vídeos sobre os perceptrons;
• Esta aula da Universidade de Oxford.