Posted on 12/01/2017

Pré-requisitos

Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.

Conteúdo

1. Introdução
2. Intuição
3. Justificativa Matemática
4. Implementação
5. Referências

Introdução

Já vimos como o problema fundamental de aprendizado de máquina e balancear capacidade e generalização. Mesmo modelos não tão complexos podem sofrer com sobre ajustamento, como vimos no tutorial passado com a regressão polinomial. Neste tutorial, daremos um passo atrás para estudar novamente regressão linear, mas agora sob uma perspectiva Bayesiana. Isso nos dará uma técnica extremamente poderosa para melhorar a generalização dos nossos modelos, sejam eles lineares, polinomiais ou até redes neurais extremamente complexas.

Intuição

Lembra da nossa fórmula para os parâmetros ótimos de regressão linear: \(\pmb{\hat{w}} = (X^T X)^{-1} X^T \pmb{y}\)? Em termos computacionais, uma etapa extremamente complexa dessa formula é inverte a matriz \((X^T X)\). Isso porque quanto mais correlacionadas form as variáveis que temos, mais \((X^T X)\) se aproxima de algo que é impossível de inverter.

Diz a lenda que, para lidar com esse problema, alguns cientistas adicionavam um pequeno valor à diagonal de \((X^T X)\), tornando sua inversão mais estável. Ao fazer isso perceberam que a performance do modelo no set de avaliação melhorava. Com o tempo, o teoria estatística se desenvolveu para explicar essa melhora e é isso que veremos aqui. A primeira coisa que precisamos reparar é que \((X^T X)\) é uma matriz de covariância, ou seja, ela contém a informação de como cada variável de \(X\) correlaciona entre si. A diagonal de \((X^T X)\) tem o resultado das covariâncias das variáveis com elas mesmas, ou seja, as variâncias das variáveis de \(X\). Assim, adicionar um pequeno valor a diagonal de \((X^T X)\) é como aumentar artificialmente a variância nos dados. Isso torna o modelo mais robusto, melhorando sua generalização.

Mais ainda, adicionar um pequeno valor \(\gamma^2\) à diagonal de \((X^T X)\) é equivalente à adicionar um termo na nossa função custo, que passa de \( (\pmb{y} - \pmb{\hat{w}}X)^T(\pmb{y} - \pmb{\hat{w}} X)\) para

Minimziar o primeiro termo da função objetivo acima corresponde a diminuir o erro no set de treino, ao passo que a minimização do segundo termo penaliza a complexidade do modelo. Com esse novo objetivo, o ponto ótimo passa a ser

\(\pmb{\hat{w}}^T \pmb{\hat{w}}\) também é chamado de norma L2 de \(\pmb{\hat{w}}\), cuja notação é \(\parallel\pmb{\hat{w}}\parallel ^2\). Do ponto de vista da otimização, isso adiciona uma segunda força, puxando o parâmetros \(w\) em direção a zero. Quanto maior for o \(\gamma\), maior será essa força e maior será a regularização do modelo. O efeito disso é uma suavização da função aprendida pelo modelo. Por outro lado, é sempre bom lembrar que se \(\gamma\) for muito grande, a regularização faz com que o modelo perca muita capacidade, sofrendo assim com muito viés.

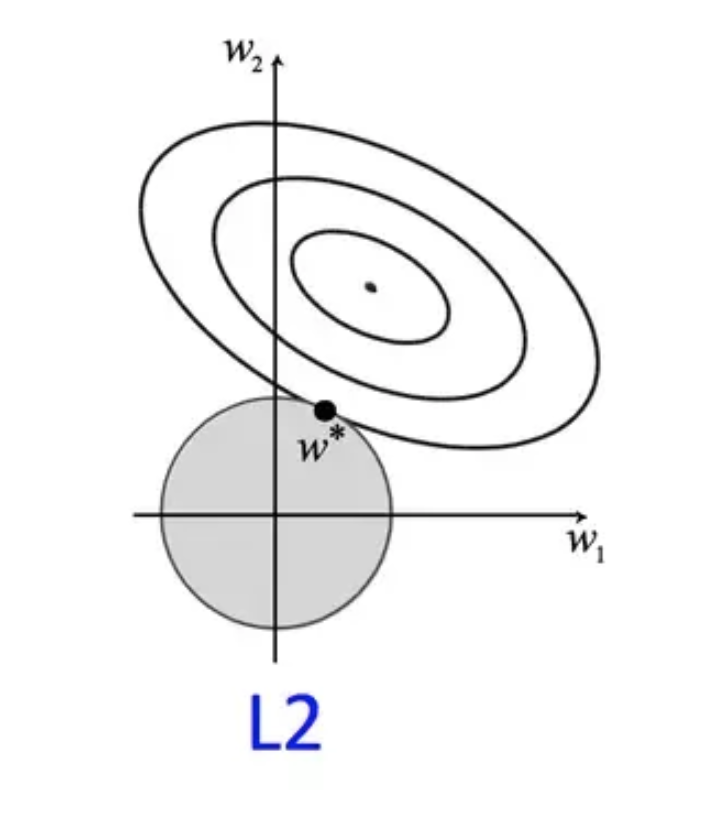
Acima, vimos que podemos adicionar um termo à minimização do custo para penalizar complexidade de modelo. Isso equivale à assumir uma variância maior nas variáveis utilizadas. Vamos agora aprofundar nas justificativas matemáticas do que chamamos regularização L2 e derivar o método de regressão de Ridge. Também veremos como interpretá-lo de uma maneira Bayesiana

Justificativa Matemática

Podemos assumir que a nossa variável \(\pmb{y}\) é determinada pelos nossos dados \(\pmb{X}\) e por parâmetros \(\pmb{w}\), que definem uma relação linear entre as variáveis independentes e dependentes. Assim, nosso objetivo é estimar a distribuição de \(\pmb{w}\). Seguindo uma abordagem Bayesiana, podemos começar com as seguintes equações

A primeira equação nos dá o que queremos modelar, isto é, a probabilidade conjunta de \(\pmb{y}\) e \(\pmb{w}\), dado os dados. Essa fórmula vem da regra da cadeia das probabilidade. A segunda equação nos dá o modelo linear, onde assumimos que \(\pmb{y}\) segue uma distribuição normal centrada na previsão \(\pmb{X} \pmb{w}\), que é dada por uma regressão linear. Por fim, a última equação é a probabilidade a priori que assumimos para os parâmetros \(\pmb{w}\). Numa perspectiva Bayesiana, \(\pmb{w}\) é uma variável aleatória e nosso objetivo é estimar sua distribuição. A distribuição a priori reflete nossas crenças sobre \(\pmb{w}\) antes de observarmos qualquer dado. Colocá-la centrada em zero significa que, até olharmos os dados, não temos razões nenhuma para acreditar que alguma variável de \(\pmb{X}\) impacta \(\pmb{y}\). Muito bem, vamos então estimar \(\pmb{w}\) a partir das equações acima.

Em primeiro lugar, da definição de probabilidade condicional, temos que a probabilidade de \(\pmb{w}\) dado \(\pmb{y}\) e \(\pmb{X}\) é igual a probabilidade de \(\pmb{w}\) e \(\pmb{y}\), dividido pela probabilidade de \(\pmb{y}\), ambas condicionadas em \(\pmb{X}\)

Podemos então maximizar a formula acima com respeito a \(\pmb{w}\) para estimar os parâmetros do nosso modelo

No primeiro passo, tiramos o denominador, já que ele não depende de \(\pmb{w}\) e não influenciará na maximização. Em seguida, aplicamos o logaritmo. Depois, usamos a regra da cadeia para obter \(P(\pmb{y}| \pmb{w}, \pmb{X})P(\pmb{w})\). Por fim, substituímos as probabilidades pela fórmula da distribuição normal. Note que \(c_1\) e \(c_1\) são apenas as constantes normalizadoras dessas distribuições e não impactam na otimização. Continuando, temos

Em que \(\lambda\) é a razão entre a variância a posteriori e a priori. Note como o primeiro termos do problema de minimização acima é exatamente igual ao de regressão linear que derivamos quando vimos MQO. O segundo termo puxa \(\pmb{w}\) para zero, penalizando a complecidade do modelo. Em aprendizado de máquina, dizemos que \(\lambda ||\pmb{w}||^2 \) é um termo de regularização. A força dessa regularização é dada pela constante \(\lambda\), que é um hiper-parâmetro tipicamente escolhido por validação cruzada. Esse hiper-parâmetro tem uma interpretação muito clara, sob a perspectiva Bayesiana. Quanto menor for a influencia que queremos dar à nossa distribuição a priori de \(\pmb{w}\), maior será \(\gamma\), indicando grande incerteza na nossa distribuição a priori, e menor será \(\lambda\).

Uma segunda forma de interpretar a força de regularização \(\lambda\) é como vimos acima. A solução analítica do problema de otimização derivado acima é

Que é chamado de estimado de Ridge. Adicionar uma constante à diagonal de \(\pmb{X}^T \pmb{X}\) é equivalente a dizer que a variância de cada variável de \(\pmb{X}\) é maior do que a observada nos dados. Isso faz com que o modelo fique mais robusto à variância.

Implementação

A implementação da regressão de Ridge involve apenas algumas pequenas mudanças no código da regressão linear tradicional. Você pode partir do código de lá, pois só mudaremos algumas linhas. Em primeiro lugar, no método de inicialização colocaremos o hiper-parâmetro \(\lambda\) de regularização. A segunda mudança é na estimação dos parâmetros ótimos. Vamos adicionar à matriz de covariância a identidade vezes \(\lambda\) (como trata-se de uma constante, não precisamos seguir o rigor de elevá-la ao quadrado).

class ridge_regression(object):

    def __init__(self, l=1e-4):
        self.l = l

    def fit(self, X_train, y_train):
        # adiciona coluna de 1 nos dados
        X = np.insert(X_train, 0, 1, 1)

        # estima os w_hat
        I = np.identity(X.shape[1]) * self.l
        w_hat = np.dot( np.dot( np.linalg.inv(np.dot(X.T, X) + I), X.T), y_train)

        self.w_hat = w_hat
        self.coef = self.w_hat[1:]
        self.intercept = self.w_hat[0]

    def predict(self, X_test):
        X = np.insert(X_test, 0, 1, 1) # adiciona coluna de 1 nos dados
        y_pred = np.dot(X, self.w_hat) # X * w_hat = y_hat
        return y_pred

A nossa implementação usa a fórmula analítica para computar \(\pmb{\hat{w}}\), mas também é possível chegar no mesmo resultado utilizando gradiente descendente para minimizar a função objetivo que definimos acima. Essa segunda alternativa é mais geral e funciona em modelos mais complexos, quando uma fórmula analítica não está disponível. Por fim, vale lembrar que a regressão de Ridge já está implementada no Scikit-Learn.

Aplicação

Podemos utilizar o que vimos acima para regularizar um modelo de regressão polinomial. Para isso, vamos partir de um código bastante parecido ao do tutorial passado. Primeiro, geramos dados segundo um polinômio de grau dois e então ajustamos um polinômio de grau 10 a esses dados. Vamos ajustar 3 desses modelos, cada um com um grau de regularização diferente. Veremos que quanto maior a regularização, mais simples fica o modelo.

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
import numpy as np
np.random.seed(42)

def f(x):
    return x**2 - 10*x + 5 + np.random.normal(0,10,size=x.shape)

# Gera os dados
x_train = np.random.uniform(0,15,15)
y = f(x_train)
X = x_train[:, np.newaxis]

# parâmetros do gráfico
colors = ['teal', 'yellowgreen', 'orange']
lw = 2

# ajusta polinômios de graus 2, 4 e 10.
for count, l in enumerate([1e-8, 1e-1, 10]):
    
    # crias as variáveis polinomiais e as passa pelo modelo de regressão de ridge
    model = make_pipeline(PolynomialFeatures(10), ridge_regression(l=l))
    model.fit(x_train.reshape(-1,1), y)
    
    # coloca as previsões no gráfico
    x_plot = np.linspace(0,15, 50)
    y_plot = model.predict(x_plot.reshape(-1,1))
    plt.plot(x_plot.reshape(-1,1), y_plot, color=colors[count], linewidth=lw,
             label="$\lambda =$ %.1e" % l)

plt.scatter(x_train, y, color='navy', s=30, marker='o')
plt.ylim([-30,90])
plt.legend(loc='best')
plt.show()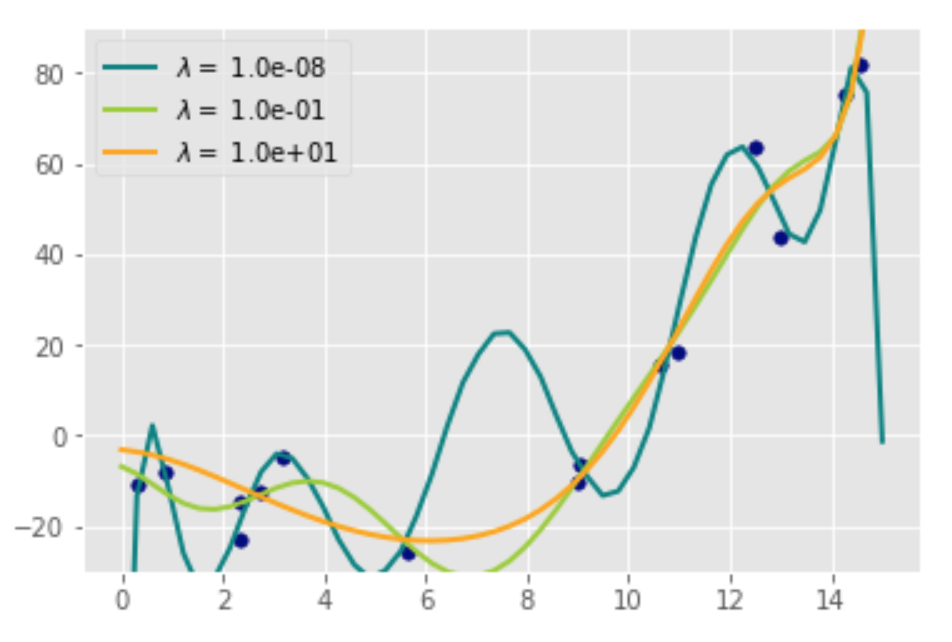

Como esperávamos, o modelo com menor regularização é extremamente complexo e, embora se ajuste perfeitamente aos dados de treino, dificilmente generalizará para outras amostrar. Conforme aumentamos a regularização, o modelo vai suavizando e se tornando mais simples, se aproximando de algo com mais viés, mas que também provavelmente generalizará melhor.

Referências

O melhor lugar para começar a aprender sobre regularização L2 e regressão de Ridge são estes vídeos do curso de Machine Learning do Andrew Ng, no Coursera. Uma vez que tenha entendido bem a intuição do modelo, este outro vídeo de Nando de Freitas fornece uma explicação matemática mais aprofundada sobre a regressão de ridge. Por fim, para uma visão Bayesiana sobre esse modelo, o curso de Bayesian Methods in Machine Learning tem um vídeo explicando a formulação matemática que desenvolvemos nesse tutorial.