Posted on 25/05/2017
Pré-requisitos
Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.
Conteúdo
- Função Custo ou Objetivo
- Como Aprendizado de Máquina difere da Otimização Pura
- Erro Quadrático Médio
- Erro Absoluto Médio
- Erro Absoluto Médio Ponderado
Função Custo ou Objetivo
Se você já viu alguns dos meus outros tutoriais 1,2,3 sobre aprendizado de máquina, deve ter reparado que sempre desenhamos algum algoritmo para minimizar alguma função. Essa função que queremos minimizar é o que chamamos de função custo ou função objetivo e normalmente é representada pela letra \( L \) (de “loss”, em inglês). Por exemplo, no caso de regressão linear, a função custo que queríamos minimizar era erro quadrático médio: \( L=(y - \hat{y})^2 \).
Até agora, eu não falei porque minimizamos essas e não outras funções, por isso pretendo cobrir essa lacuna agora. Mas antes, para evitar confusões, vamos ver como aprendizado de máquina difere do problema de otimização pura.
Como Aprendizado de Máquina difere da Otimização Pura
Se você leu minha seção de aprendizado de máquina essencial, deve lembrar que uma definição de aprendizado de máquina é quando um computador, por meio de uma experiência E, melhora sua habilidade em uma tarefa T, de acordo com alguma métrica de performance P. Tendo isso em mente, podemos dizer que aprendizado de máquina age indiretamente. Já explico. Nós queremos melhorar nossa performance P, que normalmente é definida com respeito a uma subamostra de dados de teste, mas essa métrica é geralmente inacessível diretamente, pois no momento da estimação/treinamento de um modelo de aprendizado de máquina só temos acesso à subamostra de treino. Assim, nós otimizamos P apenas indiretamente, isto é, minimizamos uma função objetivo \( L \) diferente - essa sim definida com respeito à subamostra de treino - na esperança de que fazer isso nos ajudará a melhorar P. Isso é diferente do problema puro de otimização, em que minimizar \( L \) é o objetivo em si (Goodfellow et al, 2016).
Mas como exatamente isso acontece? Quer dizer, qual é a lógica por trás de minimizar \( L \) nos ajudar a melhorar P? Aqui, vamos considerar o problema de regressão, isto é, de prever uma variável contínua como preço, risco, distância, renda, etc.
Erro Quadrático Médio
Em regressão temos um problema da forma
\[\hat{y} = y + \epsilon\]em que y é a variável que queremos prever e \( \hat{y} \) é nossa estimativa dessa variável. Agora, nós queremos prever \( y \) a partir de variáveis independentes \( \pmb{X} \). Por simplicidade, vamos supor apenas uma variável independente. Então, podemos reescrever o problema como
\[\hat{y} = f(x) + \epsilon\]em que \( f(x) \) é a função que mapeia \( x \) em \(y\) e que queremos estimar. Ainda além, nós vamos assumir que \(\epsilon\) tem média zero e é variância \(\sigma^2\). Dessa forma, podemos dizer que a probabilidade conjunta de \(y\) e \(x\) é dada por
\[P(x,y)=P(y|x)P(x)\]em que \(P(y|x)\) é a probabilidade de \(y\) dado \(x\), que segue uma distribuição tal que \(P(y|x) \sim N (\hat{y},\sigma^{2})\). Com isso, podemos provar que minimizar o erro quadrático médio gera uma estimativa \(\hat{y}\) que é um estimador de máxima verossimilhança para \(y\). A prova é um pouco complicada e não é essencial para nosso propósito aqui. De qualquer forma, deixo aqui o link dela. Basicamente, o que fazemos é usar o fato da função distribuição de probabilidade seguir uma gaussiana e então mostra-se que maximizar a probabilidade dessa gaussiana é equivalente a minimizar o erro quadrático médio, definido como
\[L=(\pmb{y} - \pmb{\hat{w}}X)^T(\pmb{y} - \pmb{\hat{w}} X)\]O que é importante perceber é que minimizar o erro quadrático médio fará com que \(\hat{y}\) será o estimador de máxima verossimilhança para \(y\), ou seja, \(\hat{y}\) será a média condicional de \(y\), \(E[y|x]\). Como assumimos que \(y\) tem uma distribuição gaussiana quando condicionado em \(x\), isso que dizer que podemos representar nossas previsão como uma reta que passa pelo ponto de maior probabilidade dessa distribuição gaussiana condicional:
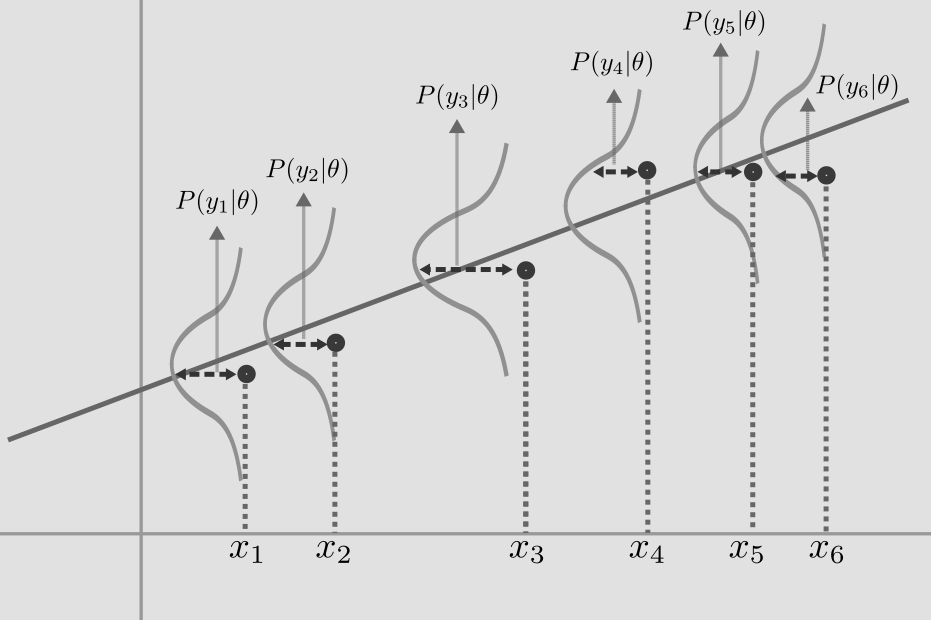
Em termos práticos, vale apena destacar alguns problemas dessa objetivo. Se por um lado ele dá a estimativa de maior probabilidade, por outro ele é extremamente sensível a outliers. Por exemplo, considere o gráfico inferior esquerdo do quarteto de Anscombe (abaixo).
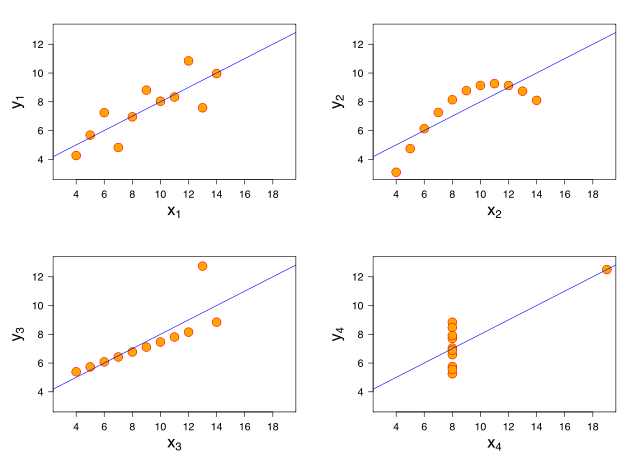
Podemos ver como a presença de um único outlier já desvia a inclinação da nossa reta estimada a ponto dela não representar bem os dados. Isso acontece pois com essa função objetivo nós estamos minimizando o quadrado dos erros, de forma que pontos muito longe da reta tem uma grande força de atração. Isso é uma propriedade da média em geral, e lembre-se de que nesse caso nossa estimativa está mirando a média condicional. Para evitar esse tipo de comportamento, podemos fazer com que nossa estimativa mire a mediana condicional, que é uma estatística robusta a presença de outliers.
Para mais detalhes sobre o principio de máxima verossimilhança e minimização do erro quadrático médio eu sugiro esta postagem.
Erro Absoluto Médio
Em vez de mirar nossa estimativa na média condicional, podemos mirá-la na mediana condicional. Para tanto, basta trocar a função objetivo de \( \frac{1}{m} \sum \epsilon^2 \) para
\[L=\frac{1}{m} \sum \|\epsilon\|\]Isto é, trocamos a minimização do erro quadrático médio para a minimização do erro absoluto médio. Podemos colocar essas duas funções custo em um gráfico para entender melhor o comportamento delas
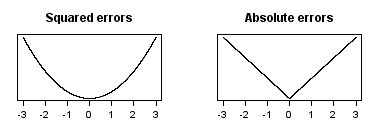
No primeiro caso, podemos ver como o custo aumenta rapidamente quando nos distanciamos do zero. Por conta disso, o objetivo de minimizar o erro quadrático médio põe muito peso em pontos distantes da previsão, sendo assim sensível aos outliers. No caso de minimizar erro absoluto médio, podemos ver como o custo cresce bem mais lentamente conforme nos distanciamos do zero. Por conta disso, utilizar o erro absoluto médio gera uma estimação robusta aos outliers. Esse tipo de estimação leva o nome de regressão quantílica, em que, particularmente, miramos na mediana, ou seja, no segundo quartil. Mas nós não precisamos nos restringir à mediana e podemos mirar em qualquer quantil.
Erro Absoluto Médio Ponderado
Em primeiro lugar, eu gostaria de deixar claro que inventei esse nome de função custo pois não achei o oficial. Isso esclarecido, nós podemos alterar a função custo de erro absoluto médio para ponderar erros positivos e negativos de forma diferente. Seja \( \tau \) um número entre 0 e 1, temos então
\[L=\begin{cases} (1-\tau) |\epsilon| & se \quad \epsilon \leq 0\\ \tau |\epsilon| & se \quad \epsilon > 0\\ \end{cases}\]Graficamente, podemos representar essa função custo da seguinte forma:
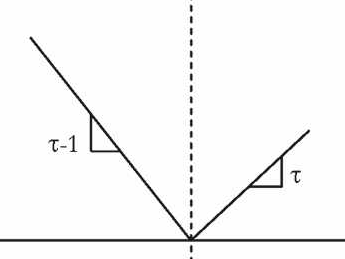
Dessa vez, o custo aumenta de forma diferente conforme nos distanciamos do zero. Por exemplo, se \(\tau\) for 0.95, erros maiores do que zero teriam um peso muito maior na otimização do custo, a inclinação da reta à direita de zero seria maior e o custo aumentaria rapidamente conforme nos distanciamos do zero para o lado positivo. Por outro lado, a inclinação da reta à esquerda seria pequena e erros menores do que zero teriam pouco impacto na otimização. Assim, minimizar essa função custo seria equivalente a mirar nossa estimativa na cauda superior da distribuição condicional de \(y\), mais precisamente, no 95º percentil. De maneira intuitiva, podemos dizer que o ponderar o erro positivo com um peso maior faz com que nossa estimativa seja empurrada para o lado positivo da distribuição, fazendo com que a maioria dos erros sejam negativos.
Por fim, podemos ver as diferentes estimativas obtidas tanto com a minimização do erro quadrático médio (em verde claro) quanto com regressão quantílica para diversos quantis.
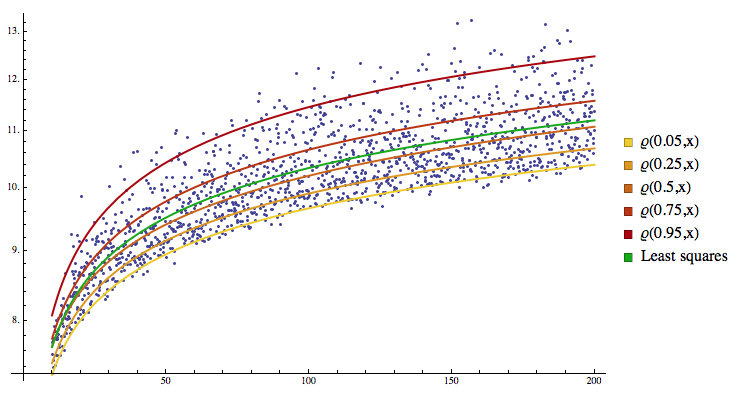
Para mais detalhes sobre regressão quantílica, sugiro esta postagem.











