Posted on 14/04/2017
Neste tutorial nós não vamos implementar nada e nenhum código será utilizado. Vou apenas explicar o que são as redes neurais artificiais, primeiro de maneira intuitiva e visual e depois com o modelo matemático. A minha intenção é desmistificar as redes neurais artificiais (RNA) como um método complexo de Aprendizado de Máquina.
Conteúdo
- Pré-Requisitos
- Neurônios
- Redes Neurais
- Deep Learning e Aprendizado de Representações
- Considerações Finais
- Referências
Pré-Requisitos
Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.
Neurônios
Um neurônio de uma rede neural é um componente que calcula a soma ponderada de vários inputs, aplica uma função e passa o resultado adiante:
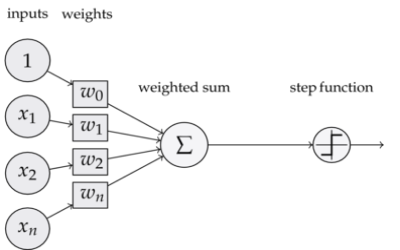
Você pode estar se lembrando dessa imagem do tutorial de regressão logística, quando falei dos perceptrons. Eu usei a mesma imagem para ressaltar que tanto regressão logística quando perceptrons são tipos de neurônios. É por isso que muitos chamam as redes neurais de multilayer perceptron. No caso da regressão logística, estamos tratando de um neurônio com uma função sigmóide após a soma ponderada. Além da regressão logística, a regressão linear também é um tipo de neurônio, só que a função após a soma ponderada é a identidade \( f(x)=x\). De forma geral, um neurônio é composto por uma transformação linear, seguida de alguma função:
\[f(\pmb{X} \pmb{w})\]Em que \( \pmb{X}\) é a matriz de dados e \( \pmb{w}\) é o vetor de parâmetros.
Redes Neurais
Intuição
Quando utilizamos vários neurônios em paralelo temos uma rede neural. Nós podemos pensar em cada neurônio como recebendo sinais das variáveis dos inputs e passando adiante uma versão ponderada e tratada desse sinal. Esses neurônios em paralelo formam uma camada oculta da rede neural. Nós podemos tratar o output de cada neurônio como uma variável do input de uma outra camada oculta. Assim, podemos empilhar camadas ocultas e produzir uma rede neural profunda:
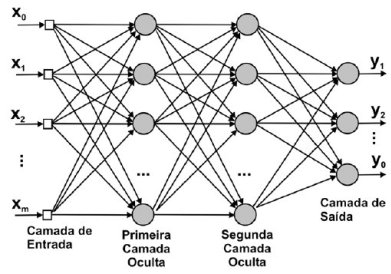
Modelo Matemático
Eu particularmente acho a imagem acima extremamente confusa e prefiro pensar nas redes neurais de outra forma: como aninhamentos sucessivos de diversas transformações lineares seguidas por alguma função diferenciável, que é aplicada elemento a elemento da matriz de entrada. Para melhor entendê-las, vamos partir de uma rede neural bem simples: um modelo de regressão linear, que pode ser entendido como uma rede neural com um único neurônio:
\[\pmb{X} \pmb{w} = \pmb{y}\] \[\begin{bmatrix} 1 & x_{11} & ... & x_{1d} \\ 1 & x_{21} & ... & x_{2d} \\ \vdots & \vdots& \vdots & \vdots \\ 1 & x_{n1} & ... & x_{nd} \\ \end{bmatrix} \times \begin{bmatrix} w_0 \\ w_1 \\ \vdots \\ w_d \\ \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \\ \end{bmatrix}\](Por simplicidade de notação, vamos omitir \( \pmb{\epsilon}\)). Para adicionar mais neurônios nessa rede neural, basta então expandir a matriz de parâmetros. Além disso, vamos multiplicar a multiplicação de matrizes por mais um vetor, mantendo a consistência do output. Temos assim o modelo de uma rede neural com mais neurônios:
\[(\pmb{X} \pmb{W_1})\pmb{w} = \pmb{y}\] \[\begin{bmatrix} 1 & x_{11} & ... & x_{1d} \\ 1 & x_{21} & ... & x_{2d} \\ \vdots & \vdots& \vdots & \vdots \\ 1 & x_{n1} & ... & x_{nd} \\ \end{bmatrix} \times \begin{bmatrix} w_{01} & w_{01} & ... & w_{0m} \\ w_{11} & w_{11} & ... & w_{1m} \\ \vdots & \vdots& \vdots & \vdots \\ w_{d1} & w_{d1} & ... & w_{dm} \\ \end{bmatrix} \times \begin{bmatrix} w_{01} \\ w_{11} \\ \vdots \\ w_{d1} \\ \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \\ \end{bmatrix}\]É importante perceber que a matriz \( \pmb{W}\) é a camada oculta da rede neural e cada coluna dessa matriz é um neurônio da camada oculta. Nós podemos pensar no vetor \( \pmb{w}\) como uma camada de saída com um único neurônio, que recebe o sinal dos neurônios anteriores, pondera-os e produz o output final da rede.
A rede neural acima não é muito interessante do ponto de vista prático pois só consegue representar funções lineares. Felizmente, podemos arrumar isso facilmente, alterando o modelo da seguinte forma:
\[\phi(\pmb{X} \pmb{W_1})\pmb{w} = \pmb{y}\]Em que \( \phi\) é alguma função não linear diferenciável. Ela precisa ser diferenciável pois vamos treinar a rede neural com gradiente descendente, assim como fizemos num tutorial passado. O tipo mais comum de função não linear que utilizamos é a unidade linear retificada, ou ReLU:
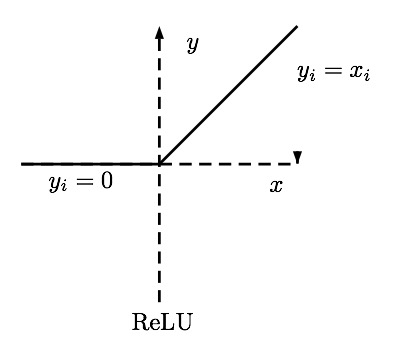
Formalmente, a ReLU é definida como \( f(x) = \max(0,x)\). Essa função tem propriedades muito interessantes, como ser parcialmente linear, o que facilita na hora do treinamento, e ter derivadas muito simples: \( 0\), se \( x < 0\) e \( 1\), se \( x > 0\). (Na prática, o ponto onde a derivada não está definida é implementado como fazendo parte de alguma das regiões onde ela é bem comportada).
Quando colocamos a não linearidade, a RNA consegue representar qualquer função, dado um número suficiente de neurônios. Quanto maior o número de neurônios, maior a capacidade do modelo. É importante ressaltar também que, quando introduzimos a não linearidade na rede neural, a função custo que otimizaremos se torna não convexa e extremamente complicada de otimizar, dificultando consideravelmente o processo de treinamento.
No modelo de RNA acima, nós só utilizamos uma camada oculta, mas nada impede que utilizemos um número maior. Por exemplo, podemos construir uma rede neural artificial com duas camadas ocultas da seguinte forma:
\[\phi(\phi(\pmb{X} \pmb{W_1})\pmb{W_2}) \pmb{w} = \pmb{y}\]Deep Learning e Aprendizado de Representações
Em Aprendizado de Máquina clássico, um problema que sempre aparece é que a
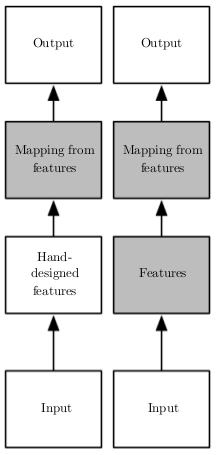
tarefa mais difícil não é treinar a máquina, mas sim engenhar variáveis que auxiliem no aprendizado. Em reconhecimento de imagem, um exemplo de como isso acontece pode ser visto nos inúmeros e nada simples pré-processamentos que a imagem passa antes de ser alimentada a um algoritmo de Aprendizado de Máquina: filtros de ruído, segmentação, aumento de contraste, detecção de contornos, etc. As redes neurais artificiais (RNAs) surgem como forma de resolver esse problema: em vez de necessitarem de alguém para criar variáveis representativas manualmente, as redes neurais são capazes de aprendê-las sozinhas. Em distinção ao Aprendizado de Máquina clássico (imagem ao lado, coluna esquerda), as redes neurais são comumente utilizadas em um novo tipo de Aprendizado de Máquina, que leva o nome de aprendizado de representações ou Deep Learning (imagem ao lado, coluna direita), no qual além de aprender um mapeamento entre características representativas e um output desejado, a máquina consegue aprender as próprias características representativas de maneira automática.
As técnicas de Deep Learning se baseiam principalmente na utilização de redes neurais profundas. Podemos pensar nas diversas camadas ocultas de uma rede neural profunda como aprendendo níveis de abstrações hierárquicos. Em reconhecimento de imagens, por exemplo, podemos pensar nas camadas mais baixas (próximas aos inputs) como aprendendo a detectar traços e variação de luminosidade, enquanto que as camadas superiores aprendem a juntar esses traços em partes de objetos. Essas partes então podem ser utilizadas por um modelo linear para discriminar entre um ou outro objetos.
No modelo matemático, podemos dizer que a parte \( \phi(\phi(\pmb{X} \pmb{W_1})\pmb{W_2})\) do modelo (ou seja, as camadas ocultas), são responsáveis por aprender variáveis representativas que ajudarão na tarefa de Aprendizado de Máquina. Nós podemos abstrair essa matrix para \( \pmb{X^*} = \phi(\phi(\pmb{X} \pmb{W_1})\pmb{W_2})\), em que \( \pmb{X^*}\) é a matriz de dados com as variáveis representativas. Em seguida, simplesmente utilizamos essas representações em conjunto com algum modelo linear:
\[\pmb{X^*} \pmb{w} = \pmb{y}\]Considerações Finais
Os modelos baseados em redes neurais artificiais são os que mais ganharam atenção nos últimos anos por conseguirem resolver problemas de IA nos quais se conseguia pouco avanço com outras técnicas. Nessa introdução às redes neurais, só falei sobre o modelo mais comum, mas saiba que as redes neurais fornecem uma flexibilidade absurda quanto a arquitetura dos modelos. Isso abre muito espaço para vários desenvolvimentos criativos por parte dos praticantes de Deep Learning com RNAs. Na minha opinião, as RNAs são a classe mais interessante de modelos de Aprendizado de Máquina por quatro motivos: (1) elas são extremamente simples, uma vez que tenhamos entendido os modelos lineares; (2) são bastante intuitivas, pois permitem a interpretação de aprendizado de níveis de abstrações hierárquicos; (3) são muito flexíveis, o que as torna ideais para resolver os mais diversos tipos de problemas; (4) são absurdamente efetivas quanto a qualidade dos resultados.
No entanto, cabe também falar sobre algumas desvantagens das redes neurais artificiais. A desvantagem mais óbvia é que os modelos baseados em RNAs são normalmente gigantescos, consumindo muita energia e recurso computacional. Em segundo lugar, treinar uma RNA é extremamente difícil, dado o formato não convexo da função custo. De fato, foi apenas recentemente (2008) que a comunidade científica conseguiu treiná-las de forma satisfatória, fazendo renascer o interesse por elas. Além disso, as RNAs estão sujeitas a sobre-ajustarem facilmente, devido a sua alta capacidade. Por conta disso, em termos práticos, quando os dados não são tão abundantes (< 10000), os resultados obtidos com RNAs não costumam ser melhores do que os obtidos com outros algoritmos de Aprendizado de Máquina.
Referências
- Esta série de vídeos explica de maneira maravilhosamente intuitiva o que são e como implementar uma RNA.
- Estes vídeos da Universidade de Stanford explicam de maneira mais detalhada a representação das RNAs.
- A Universidade de Toronto tem um curso inteiro sobre RNAs em Aprendizado de Máquina, ensinado por Geoffrey Hinton, um dos mais renomados pesquisadores na área de RNAs.
- Na verdade, as RNAs são tão populares que existem incontáveis cursos online excelentes sobre o assunto: [1], [2], [3], [4]
- Se você gosta mais de livros, este aqui é de onde tiro a maioria das minhas referências.











