Posted on 27/04/2017

Updated on 7/04/2018

Pré-Requisitos

para aprendizado de máquina</a>, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.</p>

Conteúdo

• Introdução
• Arquitetura por camadas de regressão linear
• Modularidade
• Implementação
• Próximos Passos
• Referências

Introdução

Neste tutorial vamos derivar um algoritmo de backpropagation, que será utilizado para construir e treinar redes neurais. Para manter a simplicidade, vou explicar esse algoritmo num contexto de regressão linear, mas será fácil ver como ele generaliza para redes neurais mais complexas.

Em primeiro lugar, vamos representar o modelo de regressão linear com uma arquitetura de camadas. Então, nós veremos o que cada camada precisa fazer para que seja possível minimizar o custo do nosso modelo. Já adiantando, nós vamos ver que cada camada precisará (1) computar uma função que levará de um input até um output, (2) ter um mecanismo para propagar uma derivada para trás e (3) precisará computar a derivada do output da camada com respeito aos parâmetros da camada. Com essas três operações, nós conseguiremos saber as derivadas da função custo com respeito a qualquer parâmetro do modelo. Dessa forma podemos aplicar Gradiente Descendente Estocástico e otimizar a função custo iterativamente, independentemente da arquitetura utilizada para construir o modelo.

Esse tutorial é bastante intensivo em matemática, mas você não precisa entender todos os mínimos detalhes. Eu chamarei atenção quando for falar de algo importante, que necessita mais da sua atenção. Por exemplo, é MUITO IMPORTANTE que, ao final desse tutorial, você entenda que nós não implementamos redes neurais inteiras; nós implementamos as  camadas individualmente! Guarde isso desde já e mantenha isso em mente até o final desta leitura.

Arquitetura por camadas de regressão linear

Para entender o algoritmo de backpropagation, é útil especificar o modelo que queremos treinar com uma arquitetura de camadas. Nesta introdução às redes neurais, eu mostrei como o modelo de regressão linear é também uma rede neural, embora muito simples. Aqui, vamos explicitar isso mostrando a arquitetura em camadas da regressão linear:

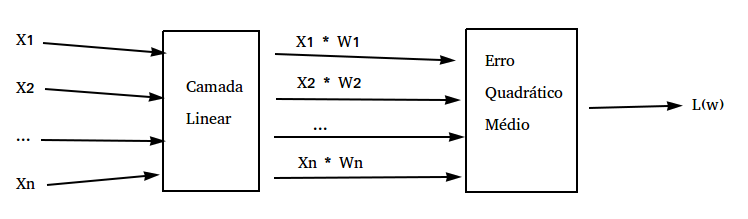
Na imagem acima, a nossa primeira camada é a camada linear, que multiplica os inputs pelos parâmetros e soma esse relutado. Matematicamente, nós podemos representar essa camada da seguinte forma:

No modelo de regressão linear, a segunda e última camada é a nossa função custo, nesse caso, o erro quadrático médio (EQM). Essa camada tira a média da diferença entre os inputs e o valor alvo observado. Matematicamente, ela é definida da seguinte forma:

As equações que definimos acima são o que chamamos de forward pass das camadas. Para utilizar backpropagation nós ainda precisamos de mais dois mecanismos em cada camada. Em primeiro lugar, como dissemos na introdução, precisamos de algum mecanismo para repassar as derivadas de trás para frente. Isso será o backward pass. Matematicamente, tudo o que precisamos definir é a derivada da função da camada com respeito aos inputs da camada. Assim, no caso da camada linear teríamos

E no caso da nossa camada de custo teríamos:

Por fim, o terceiro mecanismo que precisamos é uma forma de calcular a derivada da função da camada com respeito aos parâmetros da camada. Note que no caso de regressão linear, apenas a camada linear tem parâmetros. Assim, a derivada da camada linear com respeito aos parâmetros seria

Intuitivamente, o que queremos saber é como perturbações em \( w\) afetam a nossa função custo \( L(w)\), ou então, como \( L(w)\) e \( w\) variam juntos. Para fazer isso, nós vamos propagar as perturbações em \( L(w)\) até que elas cheguem em \( w\), ou seja, nós vamos ver como perturbações na camada de custo são reflexos de perturbações na camada linear e então veremos como que as perturbação na camada linear são reflexos de perturbações nos seus parâmetros. Assim, indiretamente, vamos saber como as perturbações nos parâmetros perturbam a função custo. Isso nos dará a direção de descida mais íngreme na função custo, ou a derivada da função custo com respeito aos parâmetros, que então será utilizada para otimização com gradiente descendente.

Modularidade

Nos agora vamos mostrar que se definirmos camadas com esses dois ou três mecanismos será possível saber a derivada da função custo com respeito a qualquer parâmetro. Primeiro, vamos entender melhor a modularidade da camada. Para isso, vamos adotar a seguinte convenção. No forward pass, uma camada \( i\) qualquer recebe como input \( z_i\) e produz como output \( z_{i+1}\). Além disso, nos vamos definir a derivada da função custo com respeito ao input da camada \( i\) como \( \delta_i\). Com isso, podemos derivar o algoritmo de backpropagation apenas em termos de \( z\) e \( \delta\), o que tornará a matemática menos carregada e a regra mais geral.

Vamos agora voltar a nossa abstração de camadas. Aqui, eu utilizarei apenas 2 camadas porque esse é o número de camadas que precisamos no nosso contexto de regressão linear, mas o que será desenvolvido valerá para qualquer número de camadas. De forma geral, o que queremos construir pode ser resumido na seguinte imagem:

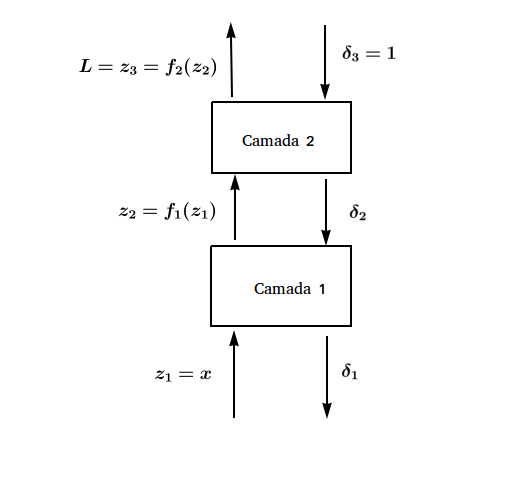
Acima, temos o forward pass na esquerda, onde começamos com \( z_1\) e o passamos adiante por duas funções, a linear e o erro quadrático médio, respectivamente. Do lado direito temos o backward pass, onde começamos com último \( \delta\), inciado sempre com 1, e propagamos as derivadas de trás para frente. Eu ainda não mostrei como faremos isso, mas é bom já ter em mente a imagem do que queremos construir. O que vou mostrar é que, para construir a arquitetura acima ou qualquer outra arquitetura, nós só precisamos implementar um módulo bem simples, da seguinte forma:

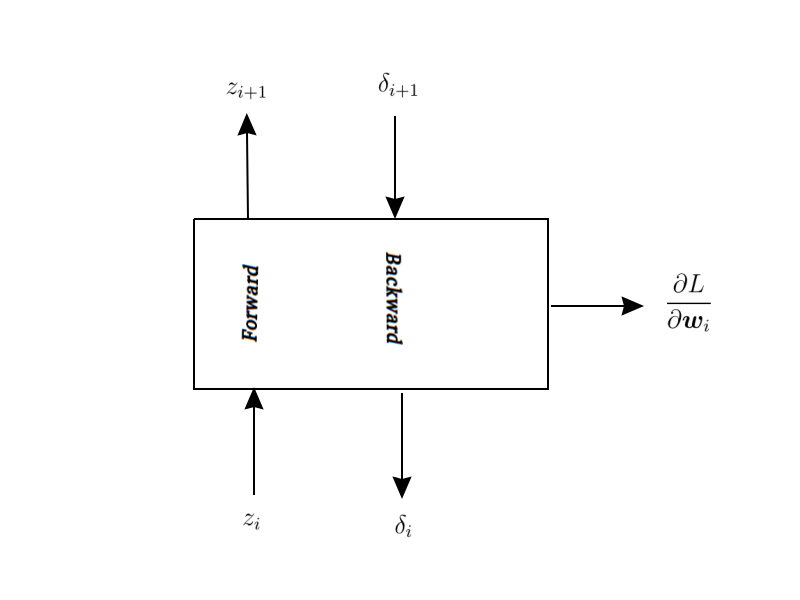
Isto é, precisamos apenas construir módulos que aceitam \( z_i\) como input e produzem \( z_{i+1}\) como output e também aceitam \( \delta_{i+1}\) e produzem \( \delta_{i}\). Além disso, ocasionalmente esses módulos terão parâmetros. Então precisaremos calcular a derivada do custo com respeito aos parâmetros.

Ok. Vamos recapitular o que temos até aqui e o que falta definir. A única coisa que temos é um esqueleto de um módulo. Falta ainda definir como passar os \( z\)s adiante, como propagar os \( \delta\)s de trás para frente e falta ainda o mais importante: achar as derivadas da função custo com respeito aos parâmetros para poder aplicar gradiente descendente. No modulo acima, isso é representado pela seta que sai para a direita. Em certo sentido, parece que não fomos muito longe, mas veremos como é simples realizar essas três operações, uma vez que tenhamos definido o módulo acima.

O primeiro mecanismo que falta definir é o forward pass. Ele é bastante simples e é definido da seguinte maneira:

Sendo \( f_i\) uma função diferenciável qualquer.

O próximo mecanismo é o backward pass. Ele é apenas um pouco mais complicado, mas nós conseguiremos chegar nele facilmente a partir da definição de \( \delta\) (lembre-se de que \( \delta_i\) é a derivada da função custo com respeito ao input \( z_i\) da camada):

Com isso, podemos ver que uma \( \delta_i\) é definido em termos do próximo \( \delta\). Essa é a sacada mais importante do algoritmo de backpropagation: definir os \( \delta\)s de forma recursiva. Assim, só precisamos iniciar o último \( \delta\) para calcular todos eles de trás para frente. Bom, mas como \( \delta_i\) é a derivada do input da camada com respeito à função custo e a última camada é o próprio custo, então o último \( \delta\) só pode ser \( 1\)! Por isso iniciamos ele dessa maneira na imagem acima.

Por fim, podemos definir o último e mais importante mecanismo:

Note que, para achar as derivadas dos parâmetros com respeito a função custo foi necessário definir antes o mecanismo que propaga os \( \delta\)s de trás para frente.

OK. Chegamos em uma parte MUITO IMPORTANTE. A equação acima nos diz que a derivada da função custo com respeito aos parâmetros de qualquer camada pode ser definida em termos do \( \delta\) da camada seguinte e da derivada do output da camada com respeito aos parâmetros da camada:

Note o poder dessa técnica. Não há nenhuma restrição quanto à arquitetura. O único requisito é que desenhemos módulos com esses três mecanismos. Então podemos organizar módulos em qualquer arquitetura conectada e sequer precisaremos nos preocupar com como calcular a derivada dos parâmetros com respeito ao custo, se os 3 mecanismos definidos acima forem implementados corretamente em cada camada. Mais ainda, essa modularidade permite um maior grau de contribuição entre pesquisadores, pois se for descoberta uma camada que melhora os resultados do modelo, ela pode ser facilmente integrada em qualquer outro modelo já existente. Dois exemplos famosos de novas camadas melhoraram significantemente a performance das redes neurais são as camadas ReLU e Dropout.

Implementação

Com essa noção de modularidade, implementar gradiente descendente fica extremamente fácil. Em vez de ter que achar de uma vez a derivada da função custo com respeito aos parâmetros, nós só precisamos empilhar camadas. Além disso, precisamos que cada camada realize 2 ou 3 operações

1. O forward pass;
2. O backward pass;
3. *Se for o caso, calcular a derivada do output da camada com respeito aos parâmetros.

Para mostrar isso, vamos recriar nosso exemplo do tutorial  de gradiente descendente, só que agora não vamos calcular as derivas à mão, mas vamos utilizar backpropagation para isso.

Primeiramente, vamos importar as dependências e simular dados exatamente como no nosso tutorial de gradiente descendente:

import pandas as pd
import numpy as np
np.random.seed(0)
from matplotlib import pyplot as plt

dados = pd.DataFrame()
dados['x'] = np.linspace(-10,10,100)
dados['y'] = 5 + 3*dados['x'] + np.random.normal(0,3,100)

Agora, vamos implementar cada camada individualmente. A primeira delas é a camada linear. Recapitulando, para essa camada teremos o forward pass:

\(f(\pmb{z}_i, \pmb{w}) = \pmb{z}_i \cdot \pmb{w} = \pmb{z}_{i+1}\)

O backward pass:

\(\delta_i = \delta_{i+1} \frac{\partial f(\pmb{z}_i)}{\partial \pmb{z}_i} = \delta_{i+1} \pmb{w}\)

E como a camada tem parâmetros, precisamos computar a derivada do custo com respeito aos parâmetros:

\(\frac{\partial L}{\partial \pmb{w}_i} = \delta_{i+1} \frac{\partial \pmb{z}_{i+1}}{\partial \pmb{w}_i} = \delta_{i+1} \pmb{z}_i\)

cclass linear(object):
    
    def __init__(self, W):
        self.W = W # [L1, L2]
    
    def forward(self, z_in):
        self.z_in = z_in # [N, L1] # cache
        self.z_out = np.dot(z_in, self.W) # [N, L2]
        return self.z_out
    
    def backward(self, d_in):
        # d_in [N, L2]
        self.dW = self.z_in.T.dot(d_in) / d_in.shape[0] # [L1, L2]
        self.d_out = d_in.dot(self.W.T) # [N, L1]
        return self.d_out

Por último, vamos definir a segunda camada, que será o erro quadrático médio. Apenas recapitulando, o forward pass seria: \(f(\pmb{z}_i) = \frac{1}{n} \sum (y-z_i)^2 =z_{i+1}\) O backward pass: \(\delta_i = \delta_{i+1} \frac{\partial f(\pmb{z}_i)}{\partial \pmb{z}_i} = -\delta_{i+1} \frac{2}{n} \sum (y-z)\)

Como vamos multiplicar o último \( \delta\) pela taxa de aprendizado, não vamos nos preocupar com a constante \( \frac{2}{n}\). Além disso, como essa é nossa última camada, nós já vamos definir o \( \delta_{i+1}\) como sendo 1.

class sqrerror(object):
    
    def __init__(self, y):
        self.y = y # [N, C]
        
    def forward(self, z_in):
        self.z_in = z_in # [N, C]
        self.z_out = np.mean(np.square(z_in - self.y), axis=0, keepdims=True) #[1, C]
        return self.z_out # [N, C]
    
    def backward(self):
        self.d_out = -1 * (self.y - self.z_in) #[100, C]
        return self.d_out

Agora só precisamos empilhar essas camadas para produzir nosso modelo de regressão linear:

class linear_regr(object):
    
    def __init__(self, learning_rate=0.0001, training_iters=100):
        # define os hiper-parâmetros
        self.learning_rate = learning_rate 
        self.training_iters = training_iters

    def fit(self, X_train, y_train, plot=False):
        
        # formata os dados
        if len(X_train.values.shape) < 2:
            X_train = X_train.values.reshape(-1,1)
        X = np.insert(X_train, 0, 1, 1)
        
        # inicia os parâmetros
        self.w_hat = np.random.normal(0, 1, size = (2,1))
        
        # constroi a arquitetura do modelo
        self.linear_layer = linear(self.w_hat) # camada linear
        self.loss = sqrerror(y_train) # camada de custo
        
        # loop de treino
        for _ in range(self.training_iters):
            
            # forward pass
            z2 = self.linear_layer.forward(X)
            self.loss.forward(z2)
            
            # backward pass
            d2 = self.loss.backward()
            self.linear_layer.backward(d2)
            
            # acha o gradiente
            gradient = self.linear_layer.dW
            gradient *= self.learning_rate # multiplica o gradiente pela taxa de aprendizado
            # atualiza os parâmetros
            self.w_hat -= gradient
                
        
    def predict(self, X_test):
        # formata os dados
        if len(X_test.values.shape) < 2:
            X = X_test.values.reshape(-1,1)
        X = np.insert(X, 0, 1, 1)
        
        return np.dot(X, self.w_hat) 
    
    
regr = linear_regr(learning_rate=0.05, training_iters=100)
regr.fit(dados['x'], dados['y'].reshape(-1,1))
regr.w_hat

array([[5.15990836],
       [2.95540097]])

Se você quer conferir como essa implementação funciona, pode baixar o projeto do meu GitHub.

Próximos Passos

Agora que entendemos o backpropagation neste contexto simples, fica fácil ver como ele se aplica às redes neurais artificiais. Nós vimos que se desenharmos corretamente pequenos componentes, podemos ligá-los para produzir uma rede que será treinada facilmente com gradiente descendente. Aqui, nossa rede foi uma simples regressão linear, mas como estamos trabalhamos com a noção de pequenos componentes, nós podemos juntar várias regressões lineares, adicionar uma camada não linear e teremos assim uma rede neural mais interessante e que poderá ser treinada da mesma forma.

A maioria dos softwares de redes neurais já implementa o backward pass em todas as operações matemáticas. Assim, nós simplesmente construímos um modelo com uma arquitetura qualquer, chamamos gradiente descendente para otimizá-lo é o backward pass é executado sem que sequer possamos perceber. Aqui, eu mostrei como implementar todo o backpropagation mas isso raramente será necessário. Mesmo assim, o que vimos acima será extremamente útil para que possamos elevar nosso nível de abstração.

Agora, quando falarmos de redes neurais, nós só vamos nos preocupar com a arquitetura do modelo, isto é, só vamos falar de como empilhar as camadas; nós vamos confiar nos softwares e ignorar a parte do backward pass. A regra será a seguinte: contanto que possamos derivar uma função, poderemos utilizá-la como uma camada. No fundo, nós sabemos que isso significa que precisamos passar os dados adiante e propagar as derivada de trás para frente, mas vamos abstrair essa informação para nos preocuparmos apenas com a construção da rede neural, e não com sua otimização. Com isso, construir redes neurais deixará de ser algo complicado e passará a ser quase como empilhar blocos de Lego de maneira criativa.

Referências

Existem muitas referências para o algoritmo de backpropagation, mas todas utilizam uma noção não modular, onde precisamos utilizar a regra da cadeia do cálculo extensivamente. Eu não gosto dessas referências porque (1) elas são mais complicadas e (2) elas não são o que de fato é implementado nos softwares.

A única referência que conheço que trata do backpropagation na forma modular é está aula excelente da universidade de Oxford, lecionada pelo professor Nando de Freitas. O meu tutorial é praticamente uma versão traduzida e simplificada da aula dele. A única diferença é que ele utiliza um contexto de regressão logística e eu preferi utilizar um de regressão linear.