Posted on 15/06/2017
Pré-requisitos
Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.
Conteúdo
Os Dados
No último tutorial, mostrei o essencial para montar uma rede neural no TensorFlow. Aqui, vamos entrar em alguns detalhes que podem ajudar a tornar o código mais organizado e fácil de entender. Novamente, vamos considerar como exemplo a rede neural para classificar imagens de dígitos escritos a mão. As imagens pertencem a 10 classes, do dígito 0 ao 9. Os dados são imagens de 28 por 28 pixeis, o que nos dá 784 variáveis. Nos tutoriais passados, nossos alvos eram vetores one-hot. Agora, eles serão simples variáveis categóricas, com a categoria 0 representando o dígito zero, a categoria 1 representando o dígito 1 e assim por diante.
import numpy as np # para computação numética menos intensiva
import os # para criar pastas
from matplotlib import pyplot as plt # para mostrar imagens
import tensorflow as tf # para redes neurais
# criamos uma pasta para salvar o modelo
if not os.path.exists('tmp'): # se a pasta não existir
os.makedirs('tmp') # cria a pasta
# baixa os dados na pasta criada e carrega os dados
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets("tmp/", one_hot=False) # repare que não usamos vetores one-hot
Escopos de Nomes
No TensorFlow, quando um nó é adicionada ao grafo, isso é feito sob um escopo. Podemos pensar nisso como o nome que atribuímos ao nó dentro do grafo. Esse nome não é necessariamente o mesmo que damos à variável no Python. Por exemplo, no grafo abaixo, definimos um nó com uma constante e atribuímos a ela o nome nome b, tanto no Python como no grafo TensorFlow. Podemos usar print() na variável definida em Python para confirmar o nome dela no grafo TensorFlow. Em seguida, nós redefinimos a constante b no Python, passando um novo nó com uma nova constante a ela. Também damos a esse nó o nome b, no TensorFlow. No entanto, quando usamos print() para confirmar o nome desse nó, não é b que aparece, mas b_0. Por que isso acontece?
graph = tf.Graph()
with graph.as_default():
# criamos constante com valor 8
b = tf.constant(8, name='b')
print(b)
# criamos constante com valor 0
b = tf.constant(0, name='b')
print(b)Tensor("b:0", shape=(), dtype=int32)
Tensor("b_1:0", shape=(), dtype=int32)
Mesmo que tenhamos redefinido a variável b, cada vez que atribuímos um nó TensorFlow a uma variável no Python, adicionamos este nó ao grafo TensorFlow. Ou seja, no Python, houve uma redefinição com sobrescrição de b, mas, no TensorFlow, ambos os nós continuam existindo e não há sobrescrição. Em vez disso, adiciona-se _1 a frente de b justamente para evitar a sobrescrição.
Agora que sabemos como os nomes das variáveis se comportam dentro do grafo TensorFlow, estamos prontos para aprender sobre os escopos dos nomes. Em poucas palavras, os escopos servem para organizar o nosso código TensorFlow (e para melhorar a visualização com o TensorBoard, como veremos mais para frente). Como recomendação de organização, devemos agrupar nós similares em um escopo próprio. Não há uma definição clara do que seja essa similaridade. Na verdade, ela é muito variável e difere de modelo para modelo. Por exemplo, suponha que tenhamos uma rede neural com 4 camadas. Cada camada terá suas variáveis W e b, além das operações de multiplicação de matriz e não linearidade. Então, em vez de ficar criando nomes para cada um desses nós, podemos agrupá-los sob um escopo da camada e dar o mesmo nome para todos eles. Vejamos como isso é feito.
# definindo constantes
lr = 0.01 # taxa de aprendizado
n_iter = 1000 # número de iterações de treino
batch_size = 128 # qtd de imagens no mini-lote (para GDE)
n_inputs = 28 * 28 # número de variáveis (pixeis)
n_l1 = 512 # número de neurônios da primeira camada
n_l2 = 512 # número de neurônios da segunda camada
n_outputs = 10 # número classes (dígitos)
graph = tf.Graph() # cria um grafo
with graph.as_default(): # abre o grafo para que possamos colocar nós
# Camadas de Inputs
with tf.name_scope('input_layer'): # escopo de nome da camada de entrada
x_input = tf.placeholder(tf.float32, [None, n_inputs], name='images')
y_input = tf.placeholder(tf.int64, [None], name='labels')
# Camada 1
with tf.name_scope('first_layer'): # escopo de nome da primeira camada
# variáveis da camada
W1 = tf.Variable(tf.truncated_normal([n_inputs, n_l1]), name='Weights')
b1 = tf.Variable(tf.zeros([n_l1]), name='bias')
l1 = tf.add(tf.matmul(x_input, W1), b1, name='linear_transformation')
l1 = tf.nn.relu(l1, name='relu')
# Camada 2
with tf.name_scope('second_layer'): # escopo de nome da segunda camada
# variáveis da camada
W2 = tf.Variable(tf.truncated_normal([n_l1, n_l2]), name='Weights')
b2 = tf.Variable(tf.zeros([n_l2]), name='bias')
l2 = tf.add(tf.matmul(l1, W2), b2, name='linear_transformation')
l2 = tf.nn.relu(l2, name='relu')
# Camada de saída
with tf.name_scope('output_layer'): # escopo de nome da camada de saída
# variáveis da camada
Wo = tf.Variable(tf.truncated_normal([n_l2, n_outputs]), name='Weights')
bo = tf.Variable(tf.zeros([n_outputs]), name='bias')
scores = tf.add(tf.matmul(l2, Wo), bo, name='linear_transformation') # logits
error = tf.reduce_mean(
tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y_input, logits=scores),
name='error')
# calcula acurácia
correct = tf.nn.in_top_k(scores, y_input, 1) # calcula obs corretas (vetor bools V ou F)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) # converte de bool para float32
# otimizador
optimizer = tf.train.AdamOptimizer(learning_rate=lr).minimize(error)
# inicializador
init = tf.global_variables_initializer()
# para salvar o modelo treinado
saver = tf.train.Saver()
# conferindo os nomes
print(y_input)
print(scores)
print(W1)
print(b1)
print(W2)Tensor("input_layer/labels:0", shape=(?,), dtype=int64)
Tensor("output_layer/linear_transformation:0", shape=(?, 10), dtype=float32)
<tf.Variable 'first_layer/Weights:0' shape=(784, 512) dtype=float32_ref>
<tf.Variable 'first_layer/bias:0' shape=(512,) dtype=float32_ref>
<tf.Variable 'second_layer/Weights:0' shape=(512, 512) dtype=float32_ref>
Acima, agrupamos nosso modelo de rede neural em 4 camadas: uma de entrada, duas camadas ocultas de neurônios com ativação ReLU e uma camada de saída. Note como mudamos a estrutura de construção do grafo, relativa a que ensinei num tutorial anterior. Daquela vez, eu disse para começarmos definindo as variáveis de todas as camadas e só então montar o modelo. Aqui, definimos as variáveis junto com a montagem do modelo. Não há uma regra geral sobre qual é a melhor forma de estruturar um programa TensorFlow. Eu costumo usar estrutura do tutorial anterior, na maioria dos casos (com definição de variáveis separada da montagem do modelo). No entanto, a forma acima faz mais sentido quando estamos organizando o código em escopos de nomes, o que geralmente é melhor com modelos muito grandes e complicados.
Vamos agora, por partes, explicar o que fizemos acima. Como sempre, primeiro definimos algumas constantes, que serão os hiper-parâmetros do nosso modelo. Depois, passamos à fase de construção do grafo, começando com a montagem do modelo, o que fazemos por camadas. Abrimos um escopo para a camada de inputs com with tf.name_scope(): e colocamos os nós de inputs - os placeholders - dentro desse escopo. Lembre-se de que os placeholders são simplesmente espaços por onde alimentaremos nosso grafo com os dados. Em seguida, abrimos o escopo da primeira camada oculta. Dentro dele, primeiro adicionamos as variáveis dessa camada e depois realizamos uma transformação linear, seguida de uma ReLU. Criamos então a segunda camada oculta de forma idêntica à criação da primeira. Por fim, abrimos um escopo para a camada de saída. Nele, criamos nós para as variáveis da camada, para os logits, para a probabilidade prevista (y_hat) e para o erro. Note que a nossa camada de output retorna logits que são vetores de tamanho 10, com cada espaço representando um escore proporcional à probabilidade prevista do dígito correspondente. No entanto, nossos alvos são variáveis categóricas no formato de um escalar, isto é, um único número. Por conta disso, usamos como custo a função com esse nome gigante sparse_softmax_cross_entropy_with_logits(). Ela faz três coisas: (1) converte os alvos de variáveis categóricas para vetores one-hot; (2) aplica a transformação softmax, que converte os logits em probabilidades (valores entre 0 e 1, somando 1); (3) calcula o custo de entropia cruzada.
Terminada a construção do nosso modelo, adicionamos nós para calcular a acurácia. A função tf.nn.in_top_k(...) vê se o alvo, passado via y_input, está entre as \( k\) mais prováveis previsões, de acordo com os escores produzidos pelo modelo. Nesse caso, estamos interessados apenas na primeira previsão mais provável, aquele dígito cuja probabilidade de estar na imagem é maior. Essa função retornará um tensor lógico, que converteremos para numérico com tf.cast e calcularemos a proporção de acertos, vendo vendo a proporção de uns (já que 1 marca um acerto). Finalizamos com um nó otimizador para treinar o modelo, um nó para iniciar as variáveis e um nó para salvar o modelo treinado. Por fim, usamos print() para verificar o nome das variáveis no grafo TensorFlow. Note como o nome do escopo é adicionado antes do nome do nó. Vamos agora para a fase de execução desse grafo. Note como ela é extremamente similar a que fizemos no tutorial passado. A única diferença é a forma como a acurácia é calculada.
# abrimos a sessão tf
with tf.Session(graph=graph) as sess:
init.run() # iniciamos as variáveis
# loop de treinamento
for step in range(n_iter+1):
# cria os mini-lotes
x_batch, y_batch = data.train.next_batch(batch_size)
# cria um feed_dict
feed_dict = {x_input: x_batch, y_input: y_batch}
# executa uma iteração de treino e calcula o erro
l, _ = sess.run([error, optimizer], feed_dict=feed_dict)
# mostra o progresso a cada 1000 iterações
if step % 1000 == 0:
x_valid, y_valid = data.validation.next_batch(512) # pega alguns dados de validação
val_dict = {x_input: x_valid, y_input: y_valid} # monta o feed_dict
# executa o nó para calcular a acurácia
error_np, acc = sess.run([error, accuracy], feed_dict=val_dict)
print('Erro de treino na iteração %d: %.2f' % (step, l))
print('Erro de validação na iteração %d: %.2f' % (step, error_np))
print('Acurácia de validação na iteração %d: %.2f\n' % (step, acc))
# salva as variáveis do modelo
saver.save(sess, "./tmp/deep_ann.ckpt")Modularidade no Código
Você deve ter reparado que o código acima é bastante repetitivo. Seria bom se pudéssemos usar um pouco de modularidade, colocando algumas partes da construção do grafo em funções. Isso pode ser feito facilmente, tornando o código muito mais fácil de manter e menos suscetível a errors de copia e cola. Abaixo, nós criamos uma função que adiciona ao grafo as variáveis de uma camada de neurônios da rede neural. Ela aceita como argumento uma matriz de variáveis, que pode ser tanto a camada de inputs na nossa rede neural quanto os outputs de uma camada intermediária (lembre-se que uma camada da rede neural trata os outputs da camada anterior exatamente como a primeira camada trata os inputs originais nos dados; afinal, o que a rede neural faz é aprender variáveis representativas ao longo das camadas). Em seguida, ainda na função, descobrimos o formato dessa matriz de inputs com inputs.get_shape(). Nós pegamos o número de colunas da matriz de inputs, ou seja, o número de variáveis, e, com isso mais o número de neurônios da camada, passado como argumento n_neurons, criamos as variáveis W e b da camada em questão. Por fim, nós realizamos a tranformação linear da camada e aplicamos a não linearidade, caso a função de ativação seja passada como argumento.
O resto do código reimplementa o mesmo gráfico que vimos acima, mas agora usando essa função para criar as camadas.
def fully_conected_layer(inputs, n_neurons, name_scope, activations=None):
'''Adiciona os nós de uma camada ao grafo TensorFlow'''
with tf.name_scope(name_scope):
# define as variáveis da camada
n_inputs = int(inputs.get_shape()[1]) # pega o formato dos inputs
W = tf.Variable(tf.truncated_normal([n_inputs, n_neurons]), name='Weights')
b = tf.Variable(tf.zeros([n_neurons]), name='biases')
# operação linar da camada
layer = tf.add(tf.matmul(inputs, W), b, name='linear_transformation')
# aplica não linearidade, se for o caso
if activations == 'relu':
layer = tf.nn.relu(layer, name='relu')
return layer
graph = tf.Graph()
with graph.as_default():
# Camadas de Inputs
with tf.name_scope('input_layer'):
x_input = tf.placeholder(tf.float32, [None, n_inputs], name='images')
y_input = tf.placeholder(tf.int64, [None], name='labels')
# Camada 1
l1 = fully_conected_layer(x_input, n_neurons=n_l1, name_scope='first_layer', activations='relu')
# Camada 2
l2 = fully_conected_layer(l1, n_neurons=n_l2, name_scope='second_layer', activations='relu')
# Camada de saída
scores = fully_conected_layer(l2, n_neurons=n_outputs, name_scope='output_layer') # logits
error = tf.reduce_mean(
tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y_input, logits=scores),
name='error')
# calcula acurácia
correct = tf.nn.in_top_k(scores, y_input, 1) # calcula obs corretas
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) # converte para float32
# otimizador
optimizer = tf.train.AdamOptimizer(learning_rate=lr).minimize(error)
# inicializador
init = tf.global_variables_initializer()
# para salvar o modelo treinado
saver = tf.train.Saver()
O que temos que ter em mente é que a função que criamos NÃO performa nenhuma computação. Ela apenas adiciona os nós (variáveis e operações) de uma camada ao grafo TensorFlow. Assim, quando chamamos l1 = fully_conected_layer(...) o que de fato fazemos é adicionar os nós da camada ao grafo. A execução do grafo construído acima é exatamente igual à anterior.
Visualização
Se você já está achando o TensorFlow uma ferramente fenomenal, agora terá certeza disso. Assim que você instala o TensorFlow, junto com ele vem o TensorBoard, uma ferramente de visualização super completa, que permite analisar o grafo criado, resumir estatísticas de erro e ver como os parâmetros evoluem. Em se tratando de redes neurais, ver o grafo pode ser muito útil para entender o fluxo de dados no interior da rede. Além disso, ver como o treinamento evolui é a melhor técnica de debugging de redes neurais. Vamos então ver como trabalhar com o TensorBoard. O primeiro passo é reformar nossa função de criar camadas de neurônios.
def fully_conected_layer(inputs, n_neurons, name_scope, activations=None):
'''Adiciona os nós de uma camada ao grafo TensorFlow'''
n_inputs = int(inputs.get_shape()[1]) # pega o formato dos inputs
with tf.name_scope(name_scope):
# define as variáveis da camada
with tf.name_scope('Parameters'):
W = tf.Variable(tf.truncated_normal([n_inputs, n_neurons]), name='Weights')
b = tf.Variable(tf.zeros([n_neurons]), name='biases')
tf.summary.histogram('Weights', W) # para registrar o valor dos W
tf.summary.histogram('biases', b) # para registrar o valor dos b
# operação linar da camada
layer = tf.add(tf.matmul(inputs, W), b, name='Linear_transformation')
# aplica não linearidade, se for o caso
if activations == 'relu':
layer = tf.nn.relu(layer, name='ReLU')
# para registar a ativação na camada
tf.summary.histogram('activations', layer)
return layerRepare que as únicas mudanças são adições de summaries (ou resumos). Primeiro, usando tf.summary.histogram(), criamos um nó para salvar histogramas dos parâmetros da camada. Depois, criamos um nó para registrar um histograma da ativação (output) da camada.
Vamos agora adicionar mais alguns nós de resumo no resto do grafo. Repare também como colocamos mais operações dentro de tf.name_scope(). Isso é feito apenas por motivo estético e tornará a visualização do nosso grafo mais agrupada. Também usamos tf.summary.scalar() para resumir a evolução de uma variável representada por um único número (ou seja, um escalar), tais como o erro em termos de entropia cruzada e em termos de acurácia.
logdir = 'logs' # nome pasta para salvar os arquivos de visualização
graph = tf.Graph()
with graph.as_default():
# Camadas de Inputs
with tf.name_scope('input_layer'):
x_input = tf.placeholder(tf.float32, [None, n_inputs], name='images')
y_input = tf.placeholder(tf.int64, [None], name='labels')
# Camada 1
l1 = fully_conected_layer(x_input, n_neurons=n_l1, name_scope='First_layer', activations='relu')
# Camada 2
l2 = fully_conected_layer(l1, n_neurons=n_l2, name_scope='Second_layer', activations='relu')
# Camada de saída
scores = fully_conected_layer(l2, n_neurons=n_outputs, name_scope='Output_layer') # logits
# camada de erro
with tf.name_scope('Error_layer'):
error = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y_input, logits=scores),
name='error')
tf.summary.scalar('Cross_entropy', error) # para registrar a função custo
with tf.name_scope("Accuracy"):
correct = tf.nn.in_top_k(scores, y_input, 1) # calcula obs corretas
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) # converta para float32
tf.summary.scalar('Accuracy', accuracy) # para registrar a função custo
# otimizador
with tf.name_scope('Train_operation'):
optimizer = tf.train.AdamOptimizer(learning_rate=lr).minimize(error)
# inicializador
init = tf.global_variables_initializer()
# para salvar o modelo treinado
saver = tf.train.Saver()
# para registrar na visualização
summaries = tf.summary.merge_all() # funde todos os summaries em uma operação
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph()) # para escrever arquivos summariesPara que não tenhamos que rodar todos os resumos individualmente na fase de execução do grafo, usamos tf.summary.merge_all() para fundir todos os nós de resumo em um só. Na fase de execução então, adicionamos o nó summaries às operações para serem executadas durante uma iteração de treino. Quando esse nó é executado, ele retorna uma string (texto) codificando a informação dos resumos naquela iteração de treino. Repare que, como executaremos os resumos durante o treino, a acurácia que será armazenada pelo TensorBoard será a de treino, referente ao mini-lote daquela iteração. Por fim, ainda na fase de construção, com tf.summary.FileWriter() criamos um nó que se encarregará de escrever a informação dos resumos no disco. Para a construção desse nó, passamos o nome de uma pasta (diretório) e passamos também o grafo que será salvo para visualização (nesse caso, o grafo que estamos construindo, que é acessado com tf.get_default_graph()).
Na fase de execução, a cada 10 iterações, vamos escrever no disco a string de informações dos resumos. Fazemos isso com o método file_writer.add_summary() do nó que criamos antes para salvar informação no disco. Escrever no disco é uma operação demorada, principalmente se seu disco rígido for um HD e não um SSD. Isso significa que usar o TensorBoard aumenta drasticamente o tempo de treinamento de uma rede neural, devendo então ser utilizado apenas quando o objetivo é a visualização em si ou debugging.
# abrimos a sessão tf
with tf.Session(graph=graph) as sess:
init.run() # iniciamos as variáveis
# loop de treinamento
for step in range(n_iter+1):
# cria os mini-lotes
x_batch, y_batch = data.train.next_batch(batch_size)
# cria um feed_dict
feed_dict = {x_input: x_batch, y_input: y_batch}
# executa uma iteração de treino e calcula o erro
l, summaries_str, _ = sess.run([error, summaries, optimizer], feed_dict=feed_dict)
# a cada 10 iterações, salva os registros dos summaries
if step % 10 == 0:
file_writer.add_summary(summaries_str, step)
file_writer.close() # fechamos o nó de escrever no disco.Agora, no local onde você rodou esse código, deve haver uma pasta com o nome logs. Na linha de comando digite
$ tensorboard --logdir logs/Isso inicializará o TensorBoard. Vá em um browser (Chrome ou Firefox) e navegue para http://localhost:6006 para proceder com a visualização. Em primeiro lugar, no TensorBoard, vá para a aba GRAPHS, para visualizarmos o grafo que construímos. Você deve ver algo como a imagem abaixo. Caso os nós de treino, de salvar e de erro estejam conectado ao grafo, você pode tirá-los para melhorar a visualização. Para isso, basta clicar com o segundo botão no nó e selecionar “Remove from main graph”.
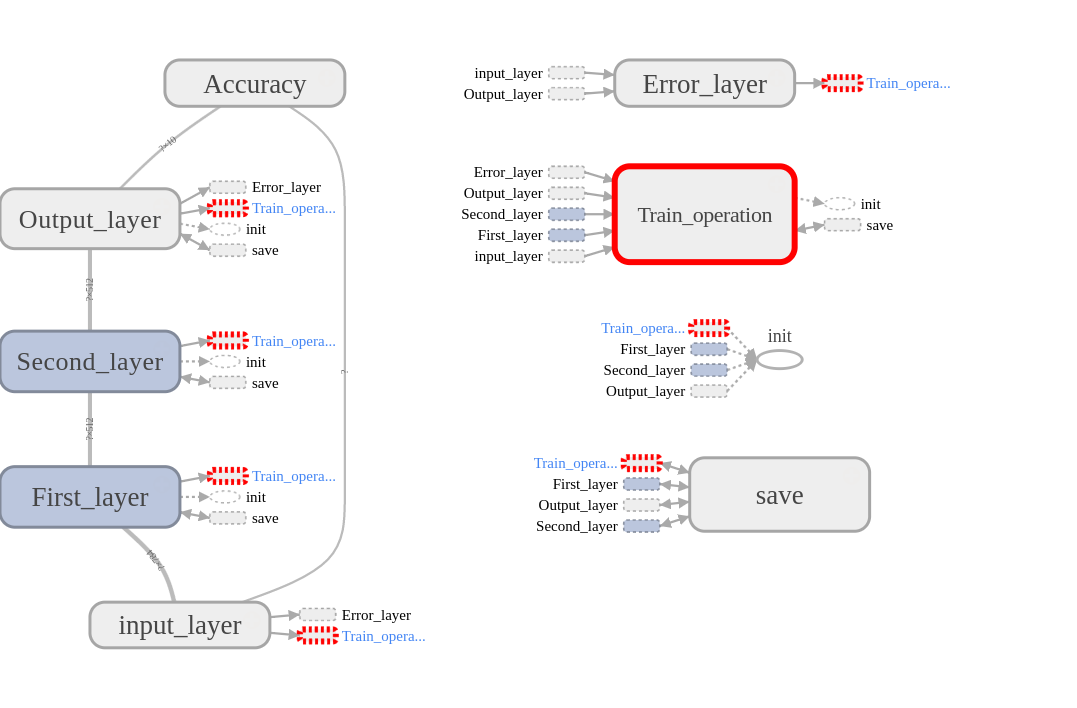
Na aba GRAPHS, podemos ver a estrutura do modelo e como os tensores fluem nesse grafo. Isso é útil caso você queira conferir se a rede neural que construiu é de fato a que tinha em mente. Note também como os nomes dos nós no grafo do TensorBoard são os mesmo que demos às nossas camadas. Se abrimos a camada, veremos como ela é construída. Quando fazemos isso, estamos olhando dentro do escopo de nome sob o qual agrupamos esta camada.
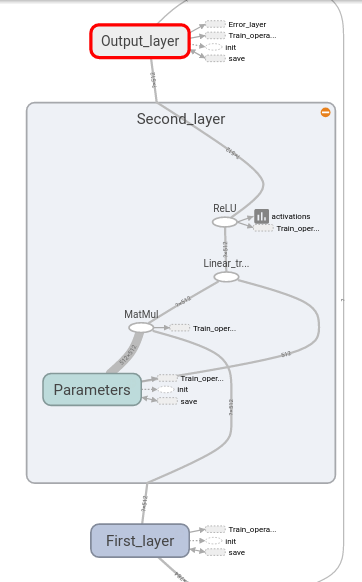
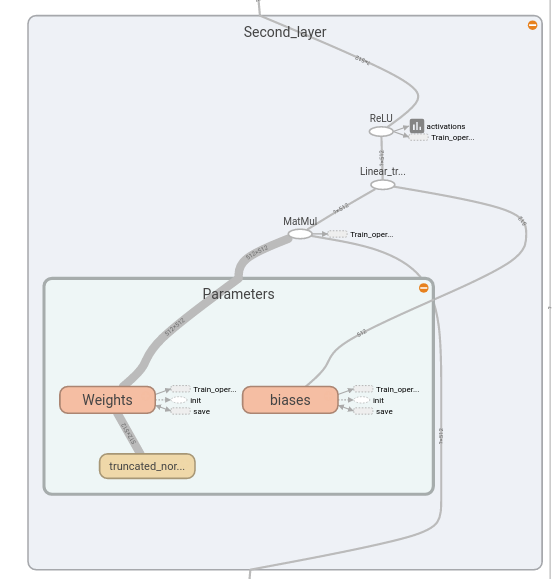
Abrindo a camada, podemos ver a função de ativação dela, podemos ver a operação linear de multiplicação de matriz \(\pmb{W}\) com adição dos viéses \(\pmb{b}\) e podemos ver como ela recebe como inputs os tensores da camada anterior e passa seus próprios outputs para a camada seguinte. Dentro da camada, lembre-se de que agrupamos a criação das variáveis dentro do seu próprio escopo de nomes, que chamamos “Parameters”. Podemos agora abrir o nó referente a esse escopo para ver como as variáveis da camada são definidas e inicializadas.
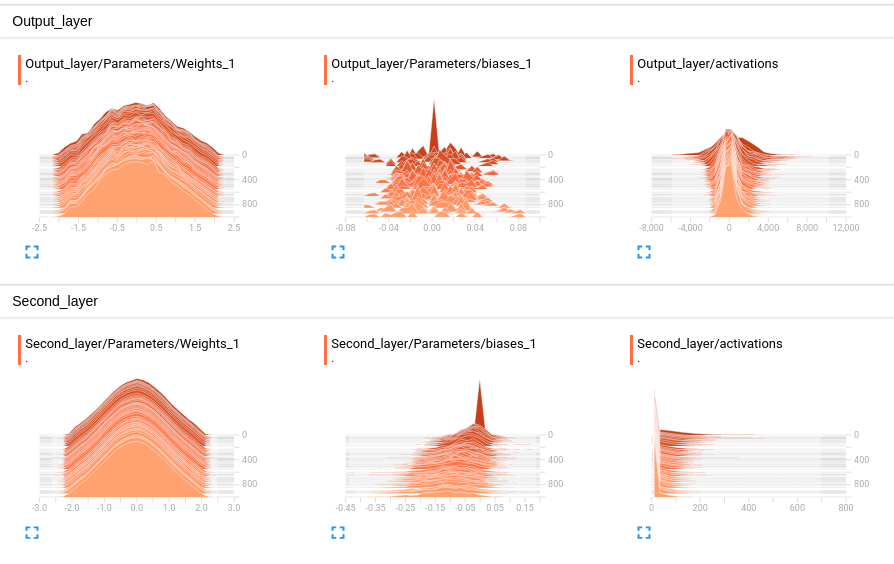
Vamos agora para a aba HISTOGRAMS. Nela, podemos ver a evolução das distribuições dos pesos, vieses e ativações de cada camada. Algo que chama atenção logo de cara é como a distribuição dos \(\pmb{W}\) mudou pouco com 1000 iterações de treino, o que indica que o treinamento só altera levemente os parâmetros. Por outro lado, a distribuição dos vieses muda mais, tornando-se achatada e quase uniforme. For fim, repare como a ativação da segunda camada tem um pico em 0, o que indica que muitos neurônios estão “mortos”, isto é, na região da ReLU em que o valor é zero e não há gradiente. Isso indica que talvez pudéssemos manter a nossa performance diminuindo o custo computacional em termos de neurônios, mas para isso precisaríamos de uma função de ativação que tivesse algum gradiente na parte negativa do seu domínio.
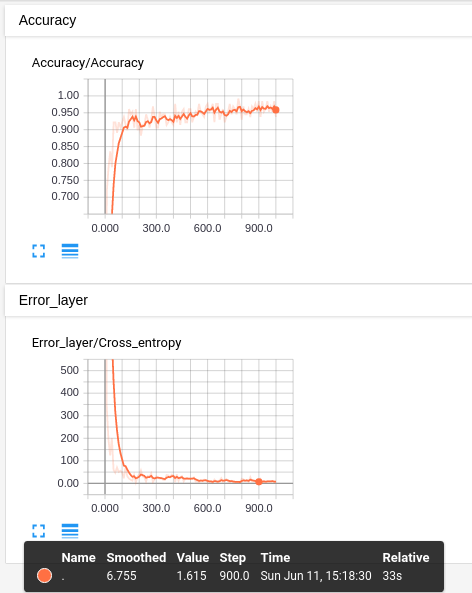
Por fim, vamos para a aba SCALARS. Nela, podemos ver como o custo e a acurácia (de treino) evoluem ao longo do treinamento. Vemos que, com bem poucas iterações de treino, menos de 200, já chegamos em uma região de custo bem baixo e com uma acurácia satisfatória. Parece que as poucas porcentagens a mais de acurácia, acima dos 90%, é o que nos da mais trabalho e toma a maior parte do treinamento.
Referências
Este tutorial foi inspirado no livro Hands-On Machine Learning with Scikit-Learn and TensorFlow, nesta séries de vídeos e nessa sessão ao vivo explicando como usar o TensorBoard. Além disso, fiz o upload do notebook usado nesse tutorial para o meu GitHub.











