Posted on 30/05/2017

Pré-requisitos

Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.

Conteúdo

1. Recapitulando
2. Dados
3. Fase de construção
4. Fase de execução
5. Simplificando o código TensorFlow
6. Referências

Recapitulando

Chamamos de neurônio um modelo matemático que calcula uma soma ponderada de sinais, aplica uma função nessa soma e passa esse sinal transformado adiante. Como exemplo de neurônios, temos o modelo de regressão linear e o modelo de regressão logística. No primeiro, a função que aplicamos na soma ponderada é a identidade, ou seja, não aplicamos função nenhuma; simplesmente passamos a soma ponderada adiante. No caso de regressão logística, aplicamos à soma ponderada uma função sigmoide (ou logística), que transforma o sinal de forma que possamos interpretá-lo como uma probabilidade. Esses dois exemplos de neurônios são modelos lineares e estão limitados a aprender relações igualmente lineares. Quando conectamos vários neurônios temos uma rede neural. Se utilizarmos uma função não linear nos neurônios da rede neural - como a ReLU, a função sigmoide ou a tangente hiperbólica -, ela terá o poder para aprender relações não lineares arbitrárias. Podemos visualizar uma rede neural como um grafo de neurônios conectados, como na imagem abaixo.

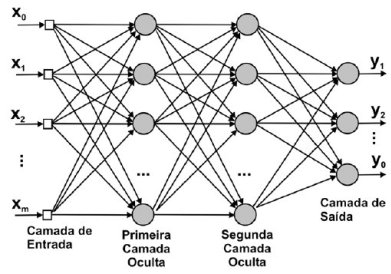
Nesse tutorial, vamos implementar uma rede neural como a da imagem. Esse tipo de rede neural é chamada de feedforward densa ou totalmente conectada, pois todos os neurônios de uma camada são conectados com todos os inputs da camada - por isso densa. Além disso, e os dados fluem em uma única direção, isto é, eles não voltam para camadas mais atrás nem dão voltas na mesma camada, - por isso  feedforward. Em termos de backpropagation, nosso forward pass será uma série de multiplicações de matrizes (transformações lineares) seguidas de alguma não linearidades. Como o TensorFlow implementa autodiferenciação, não precisaremos nos preocupar com o backward pass para computar os gradientes e realizar gradiente descendente; isso será feito automaticamente pela biblioteca de computação numérica.

Nós vimos no post introdutório de redes neurais que um modelo de rede neural artificial pode ser tão simples quanto

Aqui, vamos considerar uma pequena modificação na formulação:

Essa formulação é menos concisa mas representa o mesmo modelo. Na primeira formulação, precisamos colocar nos dados uma coluna de \(\pmb{1}\) para calcular os diversos \(\pmb{b}\)s (relembre isso no tutorial de regressão linear). Aqui, como cada camada tem seu próprio \(\pmb{b}\), é mais conveniente explicitá-los como na segunda formulação. Apenas para irmos nos acostumando com a nomenclatura técnica, lembre-se de que os \(\pmb{b}\)s são chamados de intercepto nos modelos lineares, mas nas redes neurais, nos referimos a eles como vieses (biases, do inglês).

No modelo acima, em primeiro lugar, multiplicamos os dados por uma grande matriz de parâmetros, aos que chamamos pesos (weight). Nós então adicionamos os vieses (bias) após essa multiplicação de matriz: \(\pmb{X} \pmb{W_1} + \pmb{b_1}\). Isso é uma típica transformação linear, na qual usamos operações de multiplicação e adição. Isso computa a soma ponderada de cada neurônio da camada. Após essa transformação linear, nós passamos seu resultado por alguma função não linear \(\phi\), como a ReLU. Isso resultará no output da primeira camada, \( \pmb{X}^* \), que será a atividade nos neurônios dessa camada. Nós tratamos esse output como o input da segunda camada. Então, aplicamos nele uma nova transformação linear, seguida de alguma não linearidade para obter o output da segunda camada, digamos, \( \bar{\pmb{X}} \) . Podemos repedir isso por quantas camadas quisermos, mas, nesse caso, paramos por aqui e passamos \( \bar{\pmb{X}} \) como sendo as variáveis de algum modelo linear, como uma regressão logística.

Para implementar esse modelo, vamos considerar o código desenvolvido no tutorial de TensorFlow e fazer algumas pequenas alterações. Como ponto de partida, sugiro que você simplesmente copie e cole o código de lá.

Dados

Nesse tutorial, vamos usar a base de dados MNIST. Nela, os dados são imagens em preto e branco de dígitos desenhados. A dimensão da imagem é 28 por 28 pixeis, o que nos dá 784 variáveis. O nosso alvo ou classe é o número desenhado na imagem. Em suma, trata-se de um problema de classificação multi-classes, em que o objetivo é descobrir qual digito está representado em cada imagem. Nós vamos representar o dígito alvo como vetores one-hot, com zeros em todas as casas menos na do dígito em questão. Por exemplo, o dígito 7 é representado por um vetor de zeros com 1 na oitava casa [0, 0, 0, 0, 0, 0, 0, 1, 0, 0].

Antes de iniciar esse tutorial, vamos criar uma pasta e baixar os dados necessários nela.

import numpy as np # para computação numérica menos intensiva
import os # para criar pastas

import tensorflow as tf # para redes neurais

# criamos uma pasta para colocar os dados
if not os.path.exists('tmp'):
    os.makedirs('tmp')

# baixa os dados na pasta criada 
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets("tmp/", one_hot=True) # carrega os dados já formatados

Com os dados em mãos, passamos a parte de construção de um grafo TensorFlow. Nesta fase, montaremos o nosso modelo de rede neural feedforward densa que explicamos acima. Tente ao máximo relacionar o código que escreveremos com a teória aprendida. Isso ajudará muito a entender como funciona uma rede neural e, por conseguinte, te deixará mais apto a treiná-las.

Fase de construção

Na construção do grafo, começamos definindo algumas constantes, dentre elas, os hiper-parâmetros do nosso modelo de rede neural, como taxa de aprendizado e neurônios por camadas. Depois, partimos para a construção de um grafo TensorFlow. No grafo, primeiro definimos as variáveis das matrizes de parâmetros \(\pmb{W}\). Em vez de concatenarmos uma coluna de \(\pmb{1}\) aos inputs de cada camada, vamos adicionar um vetor de vieses \(\pmb{b}\). Uma vez criadas as variáveis, vamos encadear transformações lineares com não linearidades por duas camadas. A não lineaidade será a função ReLU, que é definida em tf.nn.relu(). Por fim, passamos o output da segunda camada para um modelo de regressão logística, ao qual chamaremos de camada de output. Como esse é um problema de classificação, vamos utilizar a função custo de entropia cruzada, que será minimizada com gradiente descendente.

# definindo constantes
lr = 0.01 # taxa de aprendizado
n_iter = 4000 # número de iterações de treino
batch_size = 128 # qtd de imagens no mini-lote (para GDE)
n_inputs = 28 * 28 # número de variáveis (pixeis)
n_l1 = 512 # número de neurônios da primeira camada
n_l2 = 512 # número de neurônios da segunda camada
n_outputs = 10 # número classes (dígitos)

graph = tf.Graph() # cria um grafo
with graph.as_default(): # abre o grafo para colocar operações e variáveis

    # adiciona as variáveis da primeira camada ao grafo
    W1 = tf.Variable(tf.truncated_normal([n_inputs, n_l1]), name='Weight_1')
    b1 = tf.Variable(tf.zeros([n_l1]), name='bias_1')
    
    # adiciona as variáveis da segunda camada ao grafo
    W2 = tf.Variable(tf.truncated_normal([n_l1, n_l2]), name='Weight_2')
    b2 = tf.Variable(tf.zeros([n_l2]), name='bias_2')
    
    # adiciona as variáveis da camada de saída (ou modelo linear) grafo
    Wo = tf.Variable(tf.truncated_normal([n_l2, n_outputs]), name='Weight_o')
    bo = tf.Variable(tf.zeros([n_outputs]), name='bias_o')

    ############################################
    # Monta o modelo de rede neural artificial #
    ############################################

    # Camadas de Inputs
    x_input = tf.placeholder(tf.float32, [None, n_inputs], name='X_input')
    y_input = tf.placeholder(tf.float32, [None, n_outputs], name='y_input')

    # Camada 1
    l1 = tf.nn.relu(tf.matmul(x_input, W1) + b1, name='layer_1')
    
    # Camada 2
    l2 = tf.nn.relu(tf.matmul(l1, W2) + b2, name='layer_2')

    # Camada de *output* (regressão logística multi-classes)
    logits = tf.add(tf.matmul(l2, Wo), bo, name='output_layer')
    y_hat = tf.nn.softmax(logits) # converte scorer em probabilidades
    
    # função objetivo
    error = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_input, logits=logits, name='error'))
    
    # otimizador
    optimizer = tf.train.AdamOptimizer(lr).minimize(error)

    # inicializador
    init = tf.global_variables_initializer()

    # para salvar o modelo treinado
    saver = tf.train.Saver()

Vamos agora, parte por parte entender o que foi feito acima. Dentro do grafo, primeiro definimos as variáveis. W1 são os pesos da primeira camada. No nosso modelo, nós vamos multiplicar os dados com essa matriz, por isso ela tem o mesmo número de linhas que o número de variáveis nos dados. Além disso, o número de colunas dessa matriz definirá o número de neurônios da primeira camada da rede neural. Seja \(z_1\) os neurônios da primeira camada, temos:

Se você lembrar do algoritmo de regressão linear, poderá perceber que, antes da não linearidade, a multiplicação da matriz de dados por uma coluna da matriz de parâmetros é exatamente uma regressão linear. Assim, vemos que uma rede neural nada mais é do que várias regressões lineares seguidas de não linearidades. É simples assim, por isso estou enfatizando isso. A próxima camada é análoga a primeira: nós multiplicamos inputs por uma matriz de parâmetros W2, adicionamos b2 e aplicamos a não linearidade ReLU. As únicas diferenças entre a primeira e a segunda camada são que (1) agora os inputs não são mais os dados, mas os outputs da primeira camada, e que (2) a quantidade de neurônios (colunas de W2) é diferente. Como as atividades nos neurônios da primeira camada serão os inputs da segunda camada, a matriz de parâmetros dessa camada, W2, terá o mesmo número de linhas que os a quantidade de neurônios da primeira camada; o número de colunas de W2 definirá a quantidade de neurônios da segunda camada. Finalmente, nós passamos o output da segunda camada para um modelo linear, nesse caso, uma regressão logística. Para isso, primeiro usamos uma transformação linear: tf.add(tf.matmul(l2, Wo), bo, name='output_layer'). Essa operação gera uma pontuação para cada classe/dígito, que geralmente é chamada de logit. Note que não usamos a não linearidade aqui. Em vez disso, passamos os logits direto para uma função de achatamento softmax, que converte a pontuação em uma probabilidade válida (às vezes chamada probit), isto é, de forma que a soma da probabilidade de cada dígito resulte em 1. Isso conclui nosso modelo.

A seguir, nós definimos a função custo com tf.nn.softmax_cross_entropy_with_logits(). Essa função com um nome enorme faz duas coisas. Primeiro, converte os logits em probabilidades aplicando a função softmax e depois compara a previsão com o a classe real e retorna a função custo de entropia cruzada. Mas por que usar de novo a função softmax, se já havíamos feito isso antes? Fazemos isso por simples estabilidade computacional. Usar softmax seguida de entropia cruzada pode resultar em números com muitas casas decimais ou muito grandes, coisas que um computador não consegue representar bem. O TensorFlow tem então essa função tf.nn.softmax_cross_entropy_with_logits() para realizar de forma estável uma tranformação softmax seguida do cálculo da entropia cruzada. Tome muito cuidado para não passar o tensor y_hat de probabilidades para tf.nn.softmax_cross_entropy_with_logits(). y_hat já passou pela função softmax e passar esse tensor de novo por ela é problemático. A rede neural ainda irá treinar sem problemas, mas a performance será drasticamente reduzida e a convergência tomará muito mais tempo. Por isso, é difícil pegar esse bug e acabamos pensando que o modelo não é bom, quando na verdade erramos na especificação da função custo.

O resto do grafo não é novo. Novamente, nós criamos um otimizador para minimizar o erro, um nó para inicializar as variáveis e um saver para salvar o modelo treinado.

Fase de execução

A fase de execução pode ser reutilizada do tutorial de TensorFlow quase sem alteração. No entanto, como essa base de dados é muito grande, nós precisamos usar gradiente descendente estocástico (GDE) em vez de gradiente descendente normal. A diferença é explicada neste tutorial, mas, em poucas palavras, gradiente descendente realiza iterações mais precisas, mas o tempo de cada iteração aumenta com o tamanho da base de dados, tornando-se proibitivo para bases grades demais. Por outro lado, o tempo de uma iteração de treinamento de GDE não aumenta com o tamanho da base de dados, mas com o tamanho de um mini-lote de dados (que definimos acima). O preço que pagamos é um iteração menos precisa quanto menor for o mini-lote. Na pratica, a convergência é muito mais rápida com GDE.

Nós também vamos calcular a acurácia de validação de tempos em tempos (a cada 1000 iterações). Assim, é útil definir uma função que calcula a acurácia a partir do vetor de probabilidade de cada dígito. Para isso, vamos achar qual a posição de maior probabilidade no vetor, que nos dará o dígito previsto. Depois, vamos comparar os dígitos previstos com os verdadeiros. Nós tiramos a média dos acerto e multiplicamos por 100 para ter a percentagem de acertos. Também salvaremos os parâmetros do modelo cada 1000 iterações.

def accuracy(pred_y, true_y):
    '''Compara dois vetores one-hot para produzir a acurácia'''

    pred_labels = np.argmax(pred_y, 1) # acha o dígito de maior prob. prevista
    true_labels = np.argmax(true_y, 1) # acha o dígito verdadeiro
    
    return (pred_labels == true_labels).mean() * 100 # compara ambos


# abrimos a sessão tf
with tf.Session(graph=graph) as sess:
    init.run() # iniciamos as variáveis
    
    # loop de treinamento
    for step in range(n_iter+1):

        # cria os mini-lotes
        x_batch, y_batch = data.train.next_batch(batch_size)

        # cria um feed_dict
        feed_dict = {x_input: x_batch, y_input: y_batch}

        # executa uma iteração de treino e calcula o erro
        l, _ = sess.run([error, optimizer], feed_dict=feed_dict)
            
        # mostra o progresso a cada 1000 iterações
        if step % 1000 == 0:
            
            x_valid, y_valid = data.validation.next_batch(512) # pega alguns dados de validação
            val_dict = {x_input: x_valid, y_input: y_valid} # monta o feed_dict
            error_np, probs = sess.run([error, y_hat], feed_dict=val_dict) # calcula probabilidades e erro 
            
            print('Erro de treino na iteração %d: %.2f' % (step, l))
            print('Erro de validação na iteração %d: %.2f' % (step, error_np))
            print('Acurácia de validação na iteração %d: %.2f\n' % (step, accuracy(probs, y_valid)))

            # salva as variáveis do modelo
            saver.save(sess, "./tmp/deep_ann.ckpt")

Para calcular a acurácia, usamos np.argmax() para converter os vetores de probabilidades e o vetor one-hot nos dígitos que eles representam. Por exemplo, no caso do vetor que representa um 7 ([0, 0, 0, 0, 0, 0, 0, 1, 0, 0]), np.argmax() retorna 7, já que essa é a posição do maior número do vetor. Outro detalhe importante é passar como segundo argumento para np.argmax() o eixo para computar o máximo. No nosso caso, temos uma matriz de vetores de probabilidade empilhados. Essa matriz é do formato [n_observações, n_digitos] e nós queremos o máximo relativo ao segundo eixo. Assim, passamos 1 (o segundo eixo, lembre-se de que a contagem começa em 0) para np.argmax() e obtemos um vetor com os dígitos previstos, no formato [n_observações, 1].

Quanto a fase de execução em sí, a única novidade quanto ao tutorial passado é que não passamos todos os dados para uma iteração de otimização, mas apenas um mini-lote de dados. Por conveniência, o TensorFlow envolveu os dados em um objeto que tem um método .train.next_batch(), que nos dá o próximo mini-lote de dados. Em outros casos, nós precisamos montar os mini-lotes na mão, mas isso é bastante simples (você pode conferir como fazer isso no exercício que propus no tutorial de TensorFlow Essencial).

Com esse código e algumas poucas (4000) iterações de treino já conseguimos prever com mais de 96% de acurácia (de validação), qual dígito está representado em cada imagem (os resultados podem variar um pouco a cada execução do programa). Isso pode parecer bom, mas na verdade é uma performance bem irrisória para uma rede neural, nessa base de dados. Mais para frente, vamos ver como melhorar esses resultados.

Antes de prosseguir, vale a pena chamar a atenção para alguns erros e bugs comuns que podem aparecer. Em primeiro lugar, note como chamamos de error_np o erro de validação calculado a cada 1000 iterações. Fizemos isso pois a variável error já se referia ao nó de entropia cruzada no grafo TensorFlow. Sobreescrever um nó no grafo TensorFlow dessa forma resultará em erros nem sempre fáceis de entender, por isso tome cuidado com o nome das suas variáveis! Um outro erro comum é passar dados no formato diferente dos placeholders. Para resolver isso, eu recomendo sempre verificar o formato dos dados com algo como print(x_batch.shape).

Agora que temos nosso modelo treinado e salvo, podemos restaurá-lo para fazer previsões. A seguir, vamos avaliar a performance da nossa rede neural em 5000 exemplos do set de teste. Se seu computado tem RAM o suficiente, sinta-se a vontade para usar todo o set de teste para avaliação.

# novamente, abrimos a sessão tf
with tf.Session(graph=graph) as sess:
    
    # restauramos o valor das variáveis 
    saver.restore(sess, "./tmp/deep_ann.ckpt", )
    
    x_test, y_test = data.test.next_batch(5000)
    
    # rodamos o nó de previsão no grafo
    probs = y_hat.eval(feed_dict={x_input: x_test}) # calcula as probabilidades
    
    print('\nAcurácia de teste: %.2f' % accuracy(probs, y_test))

Eu consegui 97,12% de acurácia, mas os resultados podem variar. Lembre-se de que as variáveis são iniciadas de forma aleatória, o que gera essa instabilidade nos resultados. Para resolver isso, fixar a semente aleatória na etapa construção do grafo com tf.set_random_seed(42).

Tudo o que fizemos acima parece muito coisa, mas foram apenas poucas mudanças no código desenvolvido no tutorial de TensorFlow Essencial. Para entender melhor a implementação de uma rede neural, eu recomendo fortemente que você copie o código de lá e tente modificá-lo para rodar essa rede neural.

Simplificando o código TensorFlow

O programa desenvolvido usa as funcionalidades de mais baixo nível do TensorFlow e tem a vantagem de ser extremamente flexível. No entanto, quando só queremos montar uma simples rede neural profunda, a estrutura de código que vimos é desnecessariamente longa. Por exemplo, por que precisamos definir as variáveis de cada camada??? Não parece óbvio que, ao criar uma camada da rede neural, as variáveis já deveriam ser criadas junto??? Felizmente, o TensorFlow dispõe de um API de alto nível de abstração, chamado TF.Learn, que implementa de maneira elegante várias simplificações (não confundir com TFLearn, um API independente que também realiza simplificações). Nós vamos usar a função tf.contrib.layers.fully_connected() desse API para simplificar a construção do grafo TensorFlow. Para isso, basta passar para essa função os dados de entrada, a quantidade de neurônios e pronto, a mágica acontece.

from tensorflow.contrib.layers import fully_connected

new_graph = tf.Graph() # define um novo grafo
with new_graph.as_default(): # abre o grafo
    
    # Camadas de Inputs
    x_input = tf.placeholder(tf.float32, [None, n_inputs], name='X_input')
    y_input = tf.placeholder(tf.float32, [None, n_outputs], name='y_input')
    
    l1 = fully_connected(x_input, n_l1, scope="layer_1") # camada 1
    l2 = fully_connected(l1, n_l2, scope="layer_2") # camada 2
    
    # camada de saída
    logits = fully_connected(l2, n_outputs, activation_fn=None, scope="output_layer")
    y_hat = tf.nn.softmax(logits) # converte scorer em probabilidades
    
    # erro
    error = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_input, logits=logits, name='error'))
    
    # otimizador
    optimizer = tf.train.AdamOptimizer(lr).minimize(error)

    # inicializador
    init = tf.global_variables_initializer()

    # para salvar o modelo treinado
    saver = tf.train.Saver()

Esse grafo é exatamente igual ao que montamos antes, só que simplificado com a função fully_connected(). Como padrão, a função de ativação de fully_connected() é a ReLU, por isso, só alteramos esse argumento na camada de saída, onde não queremos nenhuma função de ativação. A função fully_connected() facilita muito na implementação de redes neurais. Com ela, não precisamos definir variáveis e o código fica bem mais limpo. Além disso, várias funcionalidades estão implementadas em fully_connected(), como formas melhores de inicializar os parâmetros, regularização, e normalização. Isso talvez não faça muito sentido ainda, mas mais para frente veremos como melhorar a convergência das redes neurais com essas ferramentas. Eu recomendo fortemente que você leia a documentação de fully_connected().

A fase de execução desse do grafo simplificado acima é exatamente a mesma que mostramos antes. Você pode simplesmente copiar e colar e tudo funcionará exatamente como antes. Só tome cuidado para mudar o nome do grafo passado à sessão com with tf.Session(graph=new_graph) as sess:.

Mas as simplificações não param por aí. A rede neural que implementamos nesse tutorial é uma das mais simples e comuns que existe. Por isso, o TensorFlow já implementou-a na forma de um classificador. Com ele, podemos dispensar completamente a estrutura de construção e execução do grafo.

from sklearn.metrics import accuracy_score # para calcular a acurácia

data = input_data.read_data_sets("tmp/", one_hot=False) # carrega os dados já formatados

x_input = tf.contrib.learn.infer_real_valued_columns_from_input(data.train.images)

deep_ann = tf.contrib.learn.DNNClassifier(hidden_units = [n_l1, n_l2], # qtd de neurônios por camada
                                         feature_columns = x_input, # var. independentes
                                         n_classes = n_outputs, # número de classes (10)
                                         activation_fn = tf.nn.relu, # função de ativação das camadas
                                         optimizer = tf.train.AdamOptimizer(learning_rate=lr)) # otimizador 

deep_ann.fit(x=data.train.images.astype(np.float32), # conversão de tipo
            y=data.train.labels.astype(np.int64), # conversão de tipo
            batch_size=128, # tamanho do mini-lote
            steps=4000) # iterações de treino

deep_ann.evaluate(data.test.images.astype(np.float32), # variáveis independentes
                  data.test.labels.astype(np.int64)) # variáveis dependentes

Ok… Esse código é extremamente abstrato. Nele, construímos uma rede neural em uma linha e a treinamos em outra. Vamos linha por linha detalhar o que está acontecendo. Nós primeiro definimos os inputs com tf.contrib.learn.infer_real_valued_columns_from_input(). O argumento dessa função são os dados de treino com as variáveis independentes. Nesse caso, data.train.images. Em seguida, criamos um classificador com tf.contrib.learn.DNNClassifier(), que é um envólucro de alto nível para abstrair todo o processo complicado de construção de uma rede neural. Os argumentos são autoexplicativos. Depois, usamos o método .fit() desse classificador. A única complicação aqui é reformatar os dados. .fit() aceita como variável independente apenas o tipo numérico float32. As variáveis dependentes \(y\) devem ser do tipo float64, por isso realizamos essas conversões. Além disso, a variável dependente \(y\) não pode ser um vetor one-hot, mas um vetor de índices representado classes. Por isso, recarregamos os dados usando agora one_hot=False. No treinamento, usamos mini-lotes de com 128 amostrar e treinamos o modelo por 4000 iterações. Note como esse classificador já toma conta de implementar a divisão dos dados em mini-lote no momento do treinamento. Finalmente, passamos ao método .evaluate() os dados e as classes de teste para avaliar o modelo.

Uma aviso final que precisa ser dado é que o módulo contrib e o API TF.Learn é um lugar de experimentação e pode mudar bastante de versão para versão do TensorFlow. Eu particularmente não gosto muito dele, pois abstrai demais e tira o controle que gosto de ter ao construir as redes neurais. Porém, para aplicações bem simples, acredito que ele possa ser útil.

Referências

Nesse tutorial, vimos diversas formas de montar uma rede neural profunda feedforward densa. Espero que com isso você se sinta confortável implementando-as com qualquer base de dados. As referências para esse tutorial são a própria documentação oficial do TensorFlow e o livro Hands-On Machine Learning with Scikit-Learn and TensorFlow.

Como recurso adicional, recomendo estar playlists de vídeos:

1) TensorFlow, por Hvass Laboratories
2) TensorFlow, por 周莫烦
3) Practical Machine Learning Tutorial with Python

Como sempre, eu coloquei o código desse tutorial no GitHub.