Funções de Ativação

Posted on 12/07/2017

Redes neurais artificiais tiveram seu advento na década de 40 mas, até pouco tempo atrás, elas eram extremamente difíceis de treinar. Esse fenômeno já era estudado desde os anos 90, mas só em 2010, com um paper de Xavier Glorot e Yoshua Bengio, é que começamos a entendemosder essa dificuldade a fundo. No tutorial passado, vimos de como surge essa dificuldade; neste tutorial vemos uma forma de mitigá-la, acelerando o treinamento de redes neurais artificiais com funções de ativação mais inteligentes.

Pré-requisitos

Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.

O Motivo da Não Linearidade

Antes de abordarmos as funções de ativação individualmente, é importante entender por que precisamos delas. Intuitivamente, as funções de ativação introduzem um componente não linear nas redes neurais, que faz com que elas possam aprender mais do que relações lineares entre as variáveis dependentes e independentes. Para ver isso, precisaremos recapitular um pouco da matemática apresentada em tutoriais passados. Considere o modelo matemático de uma rede neural clássica com duas camadas ocultas (sem perda de generalidade, vamos omitir os vieses \(\pmb{b_i}\) ):

\[y = \phi(\phi(\pmb{X}\pmb{W_1})\pmb{W_2})\pmb{w}\]

em que \(\pmb{X}\) é a matriz de dados, \(\pmb{W_i}\) são os pesos das camadas ocultas, \(\pmb{w}\) são os pesos da camada de saída e \(\phi\) é uma função não linear qualquer. Mais tarde, \(\phi\) será algumas das funções de ativação comumente usadas nas redes neurais. Por hora, vamos ver o que acontece se tirarmos \(\phi\) da equação acima.

\[\begin{aligned} y &= \pmb{X}\pmb{W_1}\pmb{W_2}\pmb{w} \\&= \pmb{X}\pmb{v} \end{aligned}\]

em que \(\pmb{v}\) será o resultado das multiplicações \(\pmb{W_1}\pmb{W_2}\pmb{w}\). Mais ainda, \(\pmb{v}\) será um vetor coluna, com o mesmo número de linhas que variáveis em \(\pmb{X}\). Agora, note como uma rede neural sem função ativação, \(y=\pmb{X}\pmb{v}\) é simplesmente um modelo de regressão linear! Assim, essa rede neural sem não linearidade está sujeita às mesmas restrições que os modelos lineares.

As funções de ativação são essenciais para dar capacidade representativa às redes neurais artificiais, introduzindo um componente de não linearidade. Por outro lado, com esse poder a mais surgem algumas dificuldades. Particularmente, ao introduzir uma ativação não linear, a superfície de custo da rede neural deixa de ser convexa, tronando a otimização mais complicada. Além disso, algumas não linearidade tornam o problema de gradientes explodindo ou desvanecendo mais evidente. A seguir, vamos focar mais como mitigar essa segunda dificuldade e deixaremos as complicações da superfície de custo para outro tutorial.

Funções de Ativação

Agora que entendemos por que precisamos das funções de ativação, vamos ver algumas das mais utilizadas em redes neurais, entender como elas se relacionam com o problema dos gradientes explodindo ou desvanecendo e discutir como podemos mudar as não linearidades para mitigá-lo. Particularmente, vamos comparar as funções Sigmoide, Tangente Hiperbólica (TanH), Unidade Linear Retificada (ReLU), Unidade Linear Exponencial (ELU) e Unidade Linear Retificada com Vazamento.

Ativação Sigmoide

A função sigmoide ou logística e sua derivada são dadas, respectivamente, por:

\[\sigma(x)=\frac{1}{1+e^x} \quad \quad \sigma'(x)=\sigma(x)(1-\sigma(x))\]

Até pouco tempo atrás, a função sigmoides era a mais utilizada em RNAs, por serem biologicamente mais plausível. Como neurônios biológicos funcionam de foma binária (ativando vs não ativando), a função sigmoide é uma boa forma de modelar esse comportamento, já que assume valores apenas entre 0 (não ativação) e 1 (ativação). No entanto, se olharmos sua derivada, podemos ver que ela satura para valores acima de 5 e abaixo de -5. Com essas derivadas tendendo a zero, a propagação do gradiente desvanece nessas regiões, causando dificuldades no treinamento.

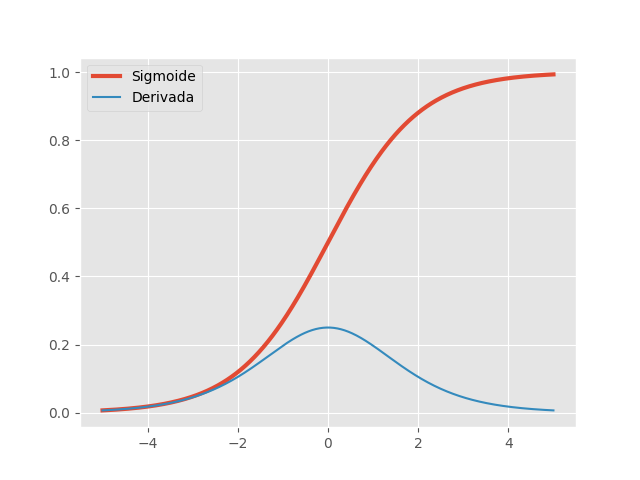
Mais ainda, repare que a derivada da função sigmoide é sempre \(<1\). Como vimos no tutorial passado, isso é problemático, fazendo com que desvaneça o produto dado pela regra da cadeia na propagação dos gradientes. Assim, não é mais recomendado utilizar a função logística como não linearidade de ativação nas redes neurais artificiais.

Ela ainda pode ser utilizada na saída da RNA, para modelar variáveis binárias. Além disso, alguns modelos probabilísticos, redes neurais recorrentes e alguns modelos não supervisionados tem restrições que tornam uma função sigmoidal necessária. No geral, a função logística praticamente desapareceu dos modelos modernos de redes neurais mais convencionais.

Ativação TanH

Similar a função sigmoide, a função Tangente Hiperbólica (TanH) também tem um formato de ‘S’, mas varia de -1 a 1, em vez de 0 a 1 como na sigmoide. A TanH se aproxima mais da identidade, sendo assim uma alternativa mais atraente do que a sigmoide para servir de ativação às camadas ocultas das RNAs. A TanH sua derivada são dadas, respectivamente, por:

\[tanh(x)=2\sigma(2x) - 1 \quad \quad tanh'(x)=1 - tanh^2(x)\]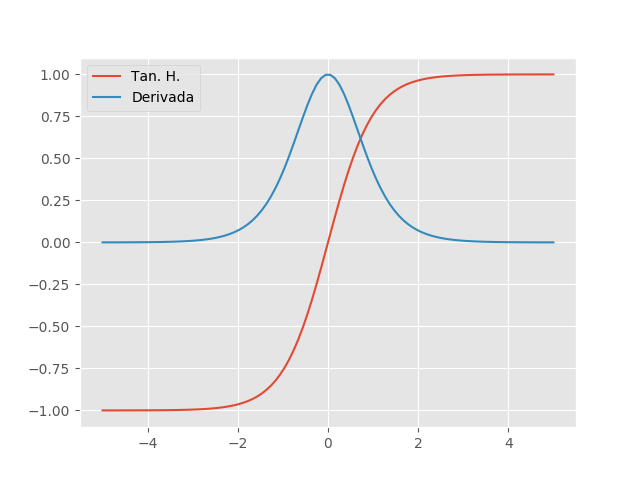

Podemos ver que as saturações ainda estão presentes, mas o valor da derivada é maior, chegando ao máximo de 1 quando \(x=0\). Por esse motivo, quando uma função sigmoidal precisa ser utilizada, recomenda-se a TanH no lugar da sigmoide.

Ativação ReLU

A ativação linear retificada (ReLU) e sua derivada são dadas, respectivamente, por:

\[ReLU(x)=max\{0, x\} \quad \quad ReLU'(x)= \begin{cases} 1, & \text{se } x\ge 0\\ 0, & \text{c.c.} \end{cases}\]

Redes com a função ReLU são fáceis de otimizar, já que a ReLU é extremamente parecida com a função identidade. A única diferença é que a ReLU produz zero em metade do seu domínio. Como consequência, as derivadas se mantêm grandes enquanto a unidade estiver ativa.

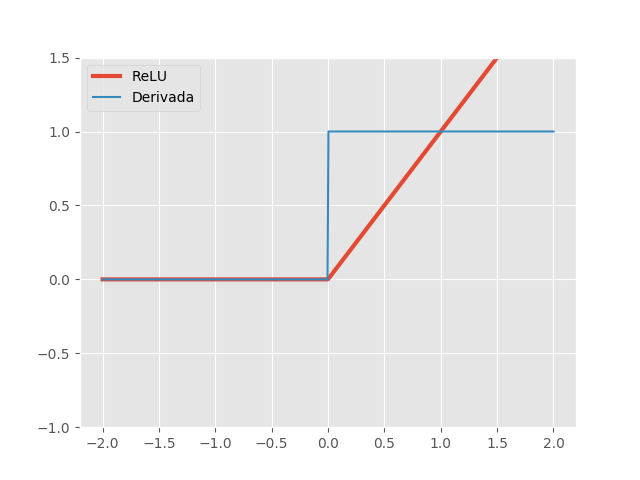
Teoricamente, a derivada não está definida em 0, mas podemos implementá-la como sendo 0 ou 1 sem maiores preocupações. Note que as derivadas não são apenas grandes, mas também estáveis, sendo 1, quando \(x>0\) e 0 quando \(x<0\). Note também que a segunda derivada é zero em todo o domínio. A ativação ReLU é muito mais eficiente do que as funções sigmoidais vistas acima e é uma das descobertas que contribuiu de forma significante para a recente popularidade de Deep Learning. Essa não linearidade é um ótimo exemplo de como a simplicidade pode ser extremamente poderosa.

Uma desvantagem da ativação ReLU é que unidades tendem a ‘morrer’ durante o treinamento, um fenômeno que faz com que o neurônio passe a produzir apenas zeros. Isso acontece quando a soma ponderada antes da aplicação da ReLU se torna negativa, fazendo com que a unidade produza zero. Nessa região, a derivada também é zero, fazendo com que os parâmetros \(\pmb{w}\) da unidade deixem de ser atualizados com gradiente descendente.

Ativação Leaky ReLU

Para solucionar o problema da ReLU, uma proposta (Maas et al, 2013) é dar uma pequena inclinação \(\alpha\) para a função na parte negativa do seu domínio. Assim, a função Leaky ReLU e sua derivada são dadas, respectivamente, por:

\[LeakyReLU(x, \alpha)=max\{\alpha x, x\} \quad \quad LeakyReLU'(x, \alpha)= \begin{cases} 1, & \text{se } x\ge 0\\ \alpha, & \text{c.c.} \end{cases}\]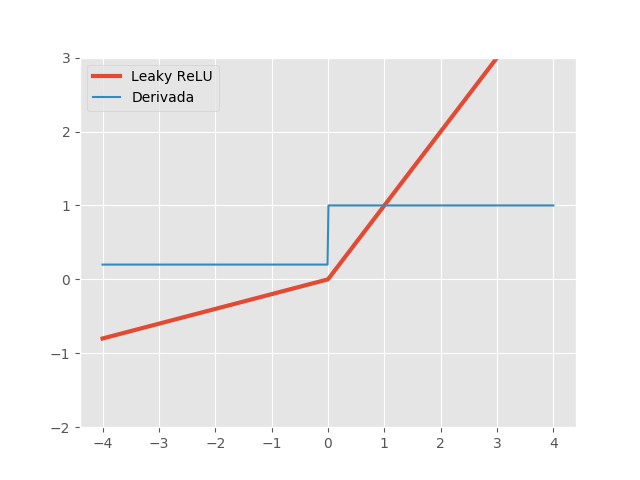

Novamente, Leaky ReLU é bastante parecida com a identidade e tem as derivadas estáveis. A novidade aqui é que a derivada na região negativa ainda é positiva, determinada por um hiper-parâmetro \(\alpha\), chamado de vazamento. Normalmente, \(\alpha\) é algum valor pequeno, como \(0,01\), mas Xu et al, 2015, mostraram que um vazamento grande, como \(0,2\), pode fornecer melhores resultados.

Ativação ELU

A última ativação que vamos ver é a unidade linear exponencial (ELU), proposta em 2015 por Djork-Arné Clevert et al. A função ELU e sua derivada são dadas, respectivamente, por:

\[ELU(x, \alpha)= \begin{cases} x, & \text{se } x\ge 0\\ \alpha(e^x - 1), & \text{c.c.} \end{cases} \quad \quad ELU'(x, \alpha)= \begin{cases} 1, & \text{se } x\ge 0\\ ELU(x, \alpha)+\alpha, & \text{c.c.} \end{cases}\]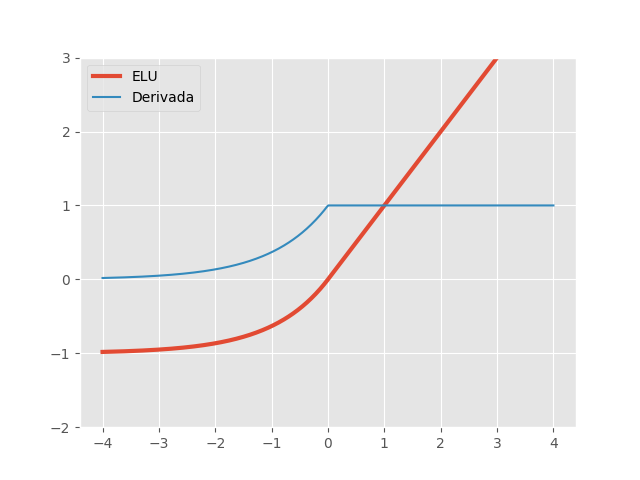

No gráfico acima, utilizamos \(\alpha=1\). Assim como a Leaky ReLU, a ativação ELU resolve o problema de unidades ‘mortas’ apresentado pelas ReLUs. Como podemos ver, a não linearidade ELU também satura na parte negativa do seu domínio. No entanto, na prática, isso não tem se mostrado um problema e ELUs são extremamente eficazes. Uma desvantagem técnica das ELUs é que computar a função exponencial é uma operação ineficiente, tornando redes neurais com ELUs um pouco mais lentas. Mesmo assim, nos estudos de Djork-Arné Clevert et al, redes com ativação ELU superaram a performance de redes com ReLUs e suas variações com vazamento.

Comparando

Vimos acima alguns fundamentos teóricos e evidências empíricas que justifiquem o uso de uma função de ativação em vez de outra. De uma forma geral devemos preferir ELU > leaky ReLU > ReLU >> tanh > sigmoide. Para tornar essa discussão mais concreta (e para não ficar apenas confiando nos estudos de outros), vamos comparar a performance de 5 redes neurais idênticas a não ser pela não linearidade nas camadas ocultas. A tarefa utilizada no experimento será reconhecimento de dígitos na base de dados MNIST.

Cada rede neural terá duas camadas ocultas com 512 neurônios cada e será treinada com gradiente descendente estocástico simples (SGD). Mais ainda, os parâmetros \(\pmb{W}\) das redes neurais serão iniciados de maneira aleatória, mas idêntica. No TensorFlow, as ativações Sigmoide, TanH, ReLU e ELU já estão implementadas e podem ser acessadas, respectivamente, por tf.nn.sigmoid, tf.nn.tanh, tf.nn.relu, tf.nn.elu. Ainda não há uma implementação da ativação Leaky ReLU, mas podemos construí-la facilmente:

def leaky_relu(z, leak=0.01):
	return tf.maximum(leak * z, z)

O resto do código é essencialmente o mesmo do tutorial de Redes Neurais Feedforward Densas, com algumas funções a mais para dar modularidade. Assim, para evitar repetições, vou omitir o código aqui. Caso queira vê-lo, está no meu GitHub.

Resultados

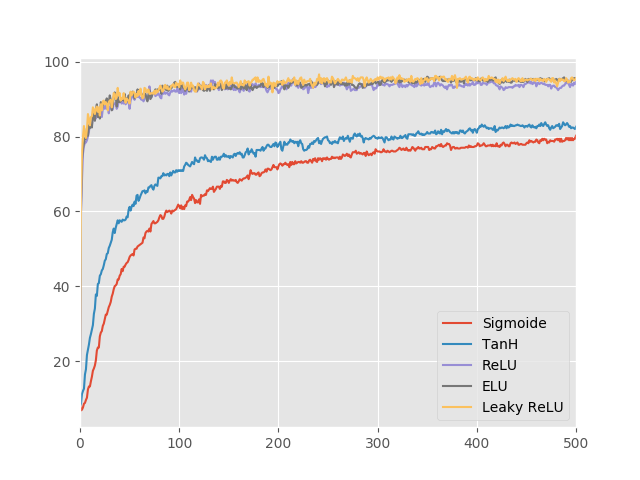
Como esperado, as funções ReLU, Leaky ReLU e ELU são muito melhores do que as funções sigmoidais. Quanto às ativações sigmoidais, a função TanH é significantemente melhor do que a Sigmoide. Isso confirma o que vimos sobre a otimização ser mais fácil com ativações que aproximam a identidade. Explorando as três melhores não linearidades, podemos ver que as performances delas são muito parecidas e precisamos ampliar o gráfico para ver qual delas é melhor.

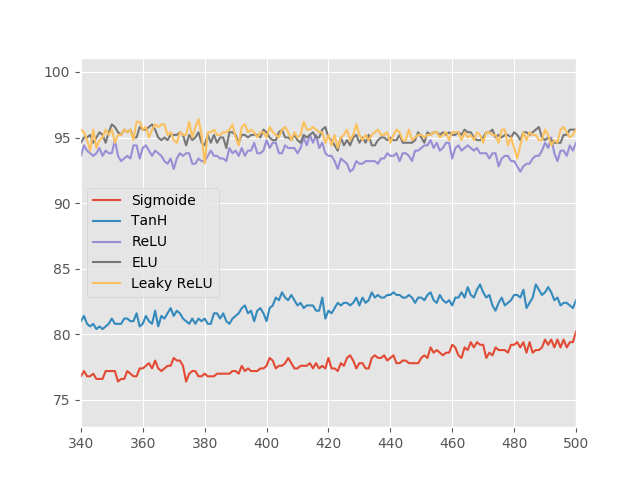
Acima, vemos que a função ReLU é apenas marginalmente pior do que a sua versão com vazamento e que a ativação ELU. Além disso, pela experiência aqui desenvolvida, não está claro se a ativação ELU é de fato melhor que a Leaky ReLU. Pode ser que nossa rede neural com apenas duas camadas não sofra tanto com os problemas de treinamento, tornando a comparação difícil. Vale também lembrar que nem todas as funções de ativação foram apresentadas aqui. Para uma lista mais completa, sugiro o artigo da Wikipédia sobre funções de ativação

Referências

Mais uma vez a referência principal do conteúdo aqui desenvolvido é o livro Deep Learning, por Goodfellow et al, 2016, especificamente, o capítulo 6 seção 6.3 sobre Unidades Ocultas. Também retirei bastante informação, principalmente considerações práticas, do livro Hands-On Machine Learning with Scikit-Learn and TensorFlow, de Aurélien Géron, 2017. Por fim, vale a pena destacar o artigo Understanding the difficulty of training deep feedforward neural networks, por Glorot e Bengio, 2010. Esse artigo representa um dos maiores avanços que tivemos nos últimos anos em entender e combater as dificuldades de treinar redes neurais artificiais. O código completo deste post pode ser encontrado no meu GitHub.