RNRs para Séries de Tempo

Posted on 27/09/2017

Pré-requisitos

Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.

Dados

Como já falamos bastante sobre Redes Neurais Recorrentes em um nível teórico, posso usar este tutorial para focar na parte de implementação desse modelo. Como exemplo, vamos usar dados de um programa de Bike Sharing (Fanaee-T, Hadi e Gama, Joao). Nosso objetivo será prever a demanda futura, isto é, a quantidade de bicicletas alugadas na hora seguinte, dado o que observamos nas últimas horas. Por favor, vá ao link acima e baixe os dados. Dentro da pasta baixada haverá um arquivo hour.csv contendo informações sobre a demanda de bicicleta a cada hora de 2011 e 2012. Os dados têm esta cara:

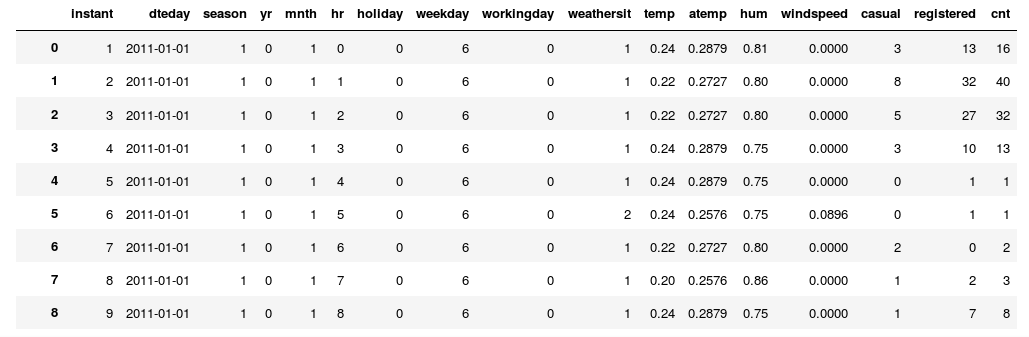
Note como os dados estão ordenados temporalmente, pelas colunas dteday e hr. Se os dados não estivessem assim, precisaríamos antes ordená-los com data.sort_values(["dteday", "hr"], inplace=True). Aqui, estamos interessados na coluna cnt, que contém o número de bicicletas alugadas naquela hora. Infelizmente, 80% do trabalho que temos com redes neurais recorrentes está no processamento dos dados para transformá-los em uma forma aceitável para o modelo. Por isso, vou gastar um tempinho a mais nessa etapa. Assim, entendendo bem esse processo, espero que você não sofra como eu sofri tentando implementar RNRs das primeiras vezes.

Formatação 3D

Redes Neurais Recorrentes recebem como entrada dados sequenciais. Isso significa que cada amostra precisa ser uma sequência, cujo formato é [períodos_de_tempo, variáveis]. Assim, quando empilharmos várias amostras para montar nossa base de dados, os mini-lotes terão um formato 3D: [n_amostras, períodos_de_tempo, variáveis]. Abaixo, começamos importando algumas dependências, lemos os dados para uma tabela e, apenas por garantia, ordenamos as linhas de maneira temporal. Em seguida armazenamos a demanda copiando a coluna cnt da tabela de dados. Então fixamos o número de períodos de tempo que terão nossas sequências de tempo. É sempre uma boa deixar essa variável no começo do código, em um local fácil de mudar, caso você queira mais tarde tentar usar uma RNR que considere mais ou menos períodos. Por fim, entramos num loop que cria uma coluna defasada para cada período de tempo. Para isso, usamos o método .shift(...) do pandas, passando como argumento o negativo da quantidade de períodos que desejamos defasar a coluna. Você pode pensar nessa operação como um deslocamento da coluna n linhas para cima.

import tensorflow as tf # para Deep Learning
import pandas as pd # para manipulação de dados
import numpy as np # para manipulação de matrizes
from matplotlib import pyplot as plt # para gráficos
from tensorflow.contrib.rnn import BasicRNNCell # para RNRs

bike_data = pd.read_csv('Bike-Sharing-Dataset/hour.csv') # lê os dados
bike_data.sort_values(["dteday", "hr"], inplace=True) # ordena temporalmente

demanda = bike_data[['cnt']] # pega a coluna de demanda
n_steps = 20 # define a quantidade de períodos de tempo

# cria n_steps colunas com a demanda defasada.
for time_step in range(1, n_steps+1):
    demanda['cnt'+str(time_step)] = demanda[['cnt']].shift(-time_step).values

demanda.dropna(inplace=True) # deleta linhas com valores nulos

Devemos lembrar que, devido ao deslocamento para cima das colunas, a operação acima faz com que surjam valores nulos nas últimas n_steps linhas da tabela. Precisamos então jogar essas linhas foras, pois não teremos as demandas y para elas. A tabela que resulta da operação acima é a seguinte.

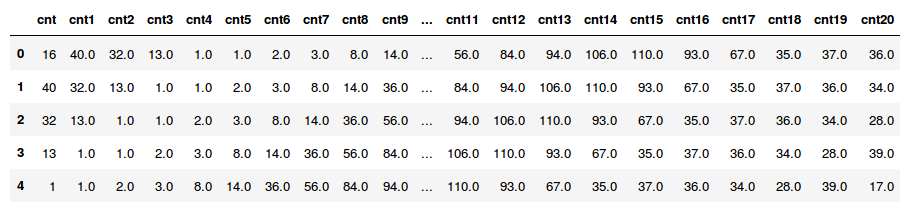
Agora podemos extrair X, as variáveis independentes, como as colunas de cnt até cnt19 e y, a variável dependente, como as colunas de cnt1 até cnt20. Assim, cada demanda x será associado com uma demanda y na hora seguinte. Também precisamos reformatar os dados para o formato [n_amostras, períodos, variáveis]. Nesse caso, como só estamos usando a demanda como variável e temos 20 períodos de tempo, o formato ficará [n_amostras, 20, 1].

X = demanda.iloc[:, :n_steps].values
X = np.reshape(X, (X.shape[0], n_steps, 1)) # adiciona dimensão

y = demanda.iloc[:, 1:].values
y = np.reshape(y, (y.shape[0], n_steps, 1))

print(X.shape, y.shape)

(17359, 20, 1) (17359, 20, 1)

Note que, como expliquei no post passado, esse é um caso de aplicação many to many, já que para cada período de tempo será feito uma previsão. Em outras palavras, tanto a entrada quanto a saída da RNR serão sequências. Podemos agora separar nossos dados 3D em treino e teste. Atenção! Como se trata de previsão, não podemos simplesmente separar aleatoriamente os dados nesses dois sets. Para que nossa análise seja uma boa aproximação do cenário real, precisamos separar os últimos dados da série de tempo para servirem de set de teste. Se isso não for feito, estaríamos usando o futuro para prever o passado, o que normalmente gera uma performance de teste superestimada e não realista.

n_test = 500

# obs: indexação negativa no Python é indexação de trás para frente
X_train, X_test = X[:-n_test, :, :], X[-n_test:, :, :]
y_train, y_test = y[:-n_test, :, :], y[-n_test:, :, :]

Agora, como vamos usar Gradiente Descendente Estocástico, precisamos embaralhar os dados de treino. Podemos fazer isso usando np.arange(0, X_train.shape[0]) para criar um array que vá de zero até a quantidade de amostras no set de treino. Esse array pode servir como uma “máscara embaralhadora”, com a qual indexamos X_train e y_train para embaralhá-los mantendo a correspondência entre eles. Isso finaliza a parte de preparação dos dados.

shuffle_mask = np.arange(0, X_train.shape[0]) # cria array de 0 a n_train
np.random.shuffle(shuffle_mask) # embaralha o array acima

# embaralha X e y consistentemente
X_train = X_train[shuffle_mask]
y_train = y_train[shuffle_mask]

Construindo a RNR

Como veremos a seguir, não serão necessárias muitas linhas de código para construir uma Rede Neural Recorrente em TensorFlow. Mesmo assim, não se engane, o código é complexo o suficiente para ter que gastar uns 3 ou quatro parágrafos explicando como ele funciona. Assim, antes de partir para o TensorFlow, vamos entender melhor a lógica recorrente que queremos implementar a partir do pseudocódigo abaixo.

X0 = X[:, 0, :] # pega os dados no primeiro período de tempo
Ht = tf.elu(tf.matmul(X0, Wx_h) + b) #  usa X0 para iniciar o estado oculto
y = [] # lista para ser preenchida com os outputs a cada período de tempo

# itera para cada período de tempo, tirando o primeiro
for t in range(1, n_steps):
  Xt = X[:, t, :] # pega os dados no próximo período
  Ht = tf.elu(tf.matmul(Xt, Wx_h) + tf.matmul(Ht, Wh_h) + b) # atualiza o estado oculto
  y.append(tf.matmul(Ht, Wh_y) + b_o)

Olhando a lógica acima, note como cada estado oculto é uma combinação do estado oculto da iteração anterior e dos dados da iteração atual. Note também como em todas as iterações usamos os mesmos parâmetros, Wx_h para conectar os dados com a camada oculta e Wh_h para conectar a camada oculta anterior com a presente. Por isso, dizemos que RNRs compartilham parâmetros através do tempo. É importante ressaltar que, na prática, não vamos utilizar loops para criar RNRs. Realizar backpropagation pelo loop acima pode gerar alguns problemas de memória, por isso vamos utilizar algumas ferramentas do TensorFlow em vez de um loop explícito. Vamos então ao código real.

Abaixo, após definir alguns hiper parâmetros do modelo e abrir o grafo TensorFlow, começamos com os tf.placeholder(...), que serão por onde alimentaremos o grafo com dados. Note como eles têm o formato de tensores 3D que expliquei acima. Em seguida, utilizamos BasicRNNCell(...) para definir o estado recorrente. Você pode pensar nesse objeto como uma “fábrica” que cria cópias de células recorrentes, isto é, desenroladas na dimensão de tempo. Passamos então essa “fábrica”, junto com o placeholder de entrada, para a função tf.nn.dynamic_rnn(...). Ela então cria os vários estados ocultos, um para cada período de tempo, e os contecta com multiplicações de matriz, da mesma forma que vimos no pseudocódigo acima. tf.nn.dynamic_rnn(...) retorna um output para cata período de tempo e o último estado oculto da rede. Neste caso, outputs[:, -1, :] = last_state, ou seja, o último estado é igual ao último output. Olhe o código abaixo com cuidado. Depois dele continuarei com a explicação da camada de saída.

n_inputs = 1 # variáveis de entrada
n_neurons = 64 # neurônios da camada recursiva
n_outputs = 1 # variáveis de entrada
learning_rate = 0.001 # taxa de aprendizado

graph = tf.Graph()
with graph.as_default():

    # placeholders
    tf_X = tf.placeholder(tf.float32, [None, n_steps, n_inputs], name='X')
    tf_y = tf.placeholder(tf.float32, [None, n_steps, n_outputs], name='y')
    
    with tf.name_scope('Recurent_Layer'):
        cell = BasicRNNCell(num_units=n_neurons, activation=tf.nn.elu)
        outputs, last_state = tf.nn.dynamic_rnn(cell, tf_X, dtype=tf.float32)
             
    with tf.name_scope('out_layer'):
        stacked_outputs = tf.reshape(outputs, [-1, n_neurons])
        stacked_outputs = tf.layers.dense(stacked_outputs, n_outputs, activation=None)
        net_outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])
    
    with tf.name_scope('train'):
        loss = tf.reduce_mean(tf.abs(net_outputs - tf_y)) # MAE
        optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(loss)

    init = tf.global_variables_initializer()

Para a camada de saída, vamos empilhar todos os estados ocultos em um tensor no formato [n_samples*n_steps, n_neurons]. Então podemos multiplicar isso por um vetor de pesos \(\pmb{w}_{n\_neurons,1}\) para produzir a camada de saída da rede. Para evitar ter que criar esse vetor de parâmetros e realizar a multiplicação, usamos tf.layers.dense(..., activation=None) para projetar o estado oculto empilhado num vetor de saída da rede neural. Por fim, desempilhamos a saída da rede novamente para o formato 3D [n_samples, n_steps, n_neurons]. Com isso, podemos comparar as previsões com os valores reais das variáveis dependente, passados por meio de um tensor também 3D, tf_y. Nesse caso, optei por usar como custo o Erro Absoluto Médio. Isso porque séries de tempo de demanda costumam ter picos e vales muito acentuados e que destoam da tendência geral. Como não quero que o modelo seja sensível a esses pontos extremos, optei por uma métrica robusta a outliers. Finalmente, definimos nosso otimizador para minimizar a função custo.

A execução do grafo acima é igual ao que já vimos em tutoriais anteriores. Primeiro, abrimos uma sessão TensorFlow e inicializamos as variáveis. Entrando no loop de treino, criamos os mini-lotes, rodamos a iteração de treino e, num certo intervalo, mostramos a performance de treino. Após todas as iterações de treino, mostramos a métrica de avaliação de teste e computamos as previsões para o set de teste.

n_iterations = 10000
batch_size = 64

with tf.Session(graph=graph) as sess:
    init.run()
    
    for step in range(n_iterations+1):
        # cria os mini-lotes
        offset = (step * batch_size) % (y_train.shape[0] - batch_size)
        X_batch = X_train[offset:(offset + batch_size), :]
        y_batch = y_train[offset:(offset + batch_size)]
        
        # roda uma iteração de treino
        sess.run(optimizer, feed_dict={tf_X: X_batch, tf_y: y_batch})
    
        # mostra o MAE de treito a cada 2000 iterações
        if step % 2000 == 0:
            train_mae = loss.eval(feed_dict={tf_X: X_train, tf_y: y_train})
            print(step, "\tTrain MAE:", train_mae)
    
    # mostra o MAE de teste no final do treinamento
    test_mae = loss.eval(feed_dict={tf_X: X_test, tf_y: y_test})
    print(step, "\tTest MAE:", test_mae)

    # realiza previsões
    y_pred = sess.run(net_outputs, feed_dict={tf_X: X_test})

 Train MAE: 196.109
  Train MAE: 34.261
  Train MAE: 31.7933
  Train MAE: 31.1256
  Train MAE: 30.2788
 Train MAE: 29.8697
 Test MAE: 26.1003

Nada mal! O erro absoluto médio no nosso set de teste é de apenas 26,1! Também podemos computar o \(R^2\) no set de teste. Apenas para que sirva para comparação, um modelo ingênuo que prevê a demanda seguinte como sendo a demanda da hora presente consegue um \(R^2\) de 0,687.

from sklearn.metrics import r2_score
r2_score(y_pred=y_pred.reshape(-1,1), y_true=y_test.reshape(-1,1))

0.911

Ótimo! Também na métrica de \(R^2\) a RNR tem uma performance excelente! mais de 20 pontos maior do que simplesmente prever a demanda futura como sendo a demanda passada. Abaixo, podemos ver as previsões no set de teste por 200 períodos de tempo.

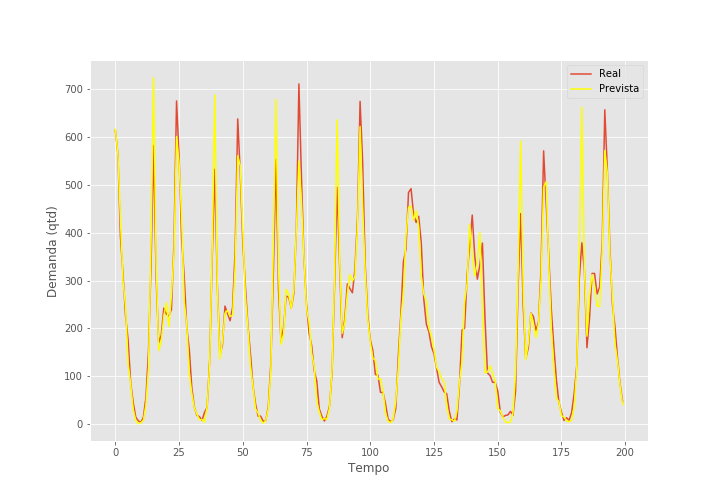
Séries de Tempo Multivariadas

Até agora, consideramos que \(\pmb{X}\) continha apenas uma variável, isto é, a demanda na hora atual. Vimos que só com isso já é possível conseguir previsões muito boas. Mas talvez poderemos usar outras variáveis e assim melhorar ainda mais nossa previsão. Além da demanda anterior, podemos também usar temperatura e umidade anteriores para tentar prever a demanda futura. Felizmente, é bastante simples alterar o código acima para incluir mais uma variável para a RNR. Começamos criando as colunas defasadas.

features = ['cnt','temp','hum'] # variáveis preditivas
demanda = bike_data[features]
n_steps = 20

for var_col in features: # para cada variável
    for time_step in range(1, n_steps+1): # para cada período
        # cria colunas da variável defasada
        demanda[var_col+str(time_step)] = demanda[[var_col]].shift(-time_step).values

demanda.dropna(inplace=True)

Em seguida, com algumas pequenas alterações é possível reformatar X novamente para um formato 3D. Note que y permanece igual, então não há necessidade de mexer nele aqui.

n_var = len(features)
columns = list(filter(lambda col: not(col.endswith("%d" % n_steps)), demanda.columns))

X = demanda[columns].iloc[:, :(n_steps*n_var)].values
X = np.reshape(X, (X.shape[0], n_steps, n_var))
print(X.shape, y.shape)

Todo o resto do código, tanto a parte de separação em dados de treino e teste, quanto a parte de construção do grafo e sua execução permanecem inalteradas. A úncia linha que precisamos mudar é, na construção do grafo, alterar a quantidade de variáveis para a RNR n_inputs = n_var. Se treinarmos a rede com mais variáveis, o seguinte relatório é mostrado.

 Train MAE: 194.996
  Train MAE: 20.707
  Train MAE: 16.1996
  Train MAE: 14.9824
  Train MAE: 14.4306
 Train MAE: 14.058
 Test MAE: 11.5745

Excelente! O resultado com as mais duas variáveis preditivas é muito melhor! Mais ainda, seu \(R^2\) é 0.972, o que é realmente excepcional! Para ser honesto, eu mesmo não acreditei quando vi esses resultados e achei que havia algum bug no código. Até agora, não achei nenhum erro, mas se você também está achando esses números bons demais para serem verdade, lhe convido a procurar uma falha e me aviar caso encontre. Finalizo com o gráfico de previsões para esse último experimento.

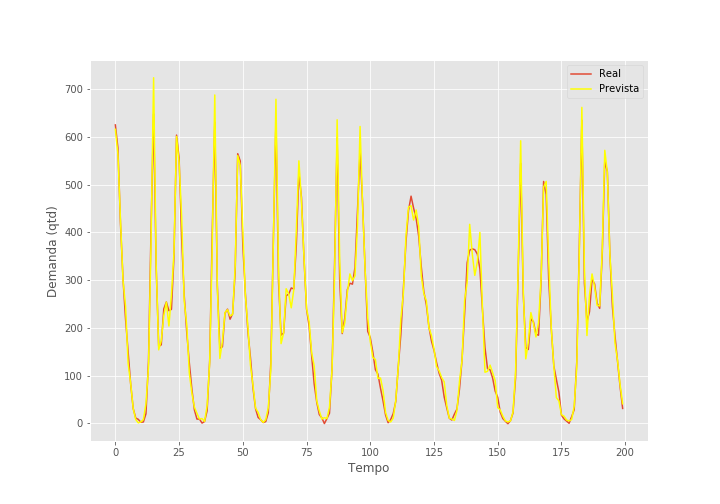
OBS: Não sei se você percebeu, mas há um pequeno vazamento no set de teste. As primeiras 19 amostras de y_test se sobrepõe as últimas 19 amostras de y_train. Num set de 500 amostras, esse vazamento sozinho não é motivo para grandes preocupações.

Referências

Usar RNRs para problemas de regressão é algo extremamente novo e tive (ainda tenho) grande dificuldade em achar fontes sólidas com esse tipo de aplicação. A maioria das referências que conheço para implementação de RNRs serão para problemas de classificação. Apenas para se ter uma ideia de como classificação domina completamente problemas de regressão quando se trata de RNRs, o livro mais conhecido sobre Redes Neurais Recorrentes, Supervised Sequence Labelling with Recurrent Neural Networks (Graves, 2012), fala exclusivamente de classificação. Por isso, caso você encontre uma referência sólida, de algum acadêmico importante na área, por favor me avise.

Por outro lado, sobram tutoriais na internet falando de implementação de RNRs para os mais diversos problemas. No canal do YouTube do Siraj exitem vários exemplos de aplicações de RNRs com tutorial em TensorFlow. Há também alguns vídeos dedicados a RNRs nesta série de tutoriais sobre Aprendizado de Máquina e Python. Este post do blog R2RT também me ajudou muito quando estava aprendendo RNRs. Além disso, como de costume, o código completo deste tutorial está no meu GitHub.

Fun fact: o exemplo usado neste tutorial serviu de base para o meu primeiro post neste blog. Eu quase sinto vergonha quando olho o código onde implementei a RNR, mas vou deixar ele lá para mostrar um pouco do avanço que tive com o tempo. Naquela época, consegui resultados muito piores do que os deste tutorial. O que me lembra de dar um aviso final muito importante: RNRs são incrivelmente difíceis de treinar. Quando você olha uma RNR implementada por outra pessoa, com tudo funcionando perfeitamente e com bons resultados, é difícil pensar que aquela pessoa gastou muito, mas muito tempo, otimizando a rede neural. Por isso, não desanime quando você tentar aplicar RNRs no seus problemas. Provavelmente levará um bom tempo de prática até que consiga um resultado minimamente apresentável.