Posted on 10/07/2017

Pré-requisitos

Vou pressupor que você tenha os conhecimentos especificados no tutorial sobre matemática e programação para aprendizado de máquina, isto é, que sabe cálculo (derivadas), o básico de álgebra linear, de estatística e de programação. Eu também vou pressupor que você viu os tutoriais anteriores a esse. Meus tutoriais são ordenados de maneira lógica e sugiro fortemente que você se atenha à ordem deles para maior compreensão.

Conteúdo

1. Gradientes Explodindo e Desvanecendo
2. As Primeiras Redes Neurais Artificiais
3. Resultados

Gradientes Explodindo e Desvanecendo

Como vimos no tutorial de backpropagation, para treinar redes neurais, computamos as derivadas de \(W_i\) com respeito ao custo e atualizamos \(W_i\) na direção oposta. Mais ainda, vimos que para conseguir as derivadas das camadas mais baixas da rede neural, utilizamos a regra da cadeia da diferenciação. Apenas para relembrar, dada uma rede neural com quatro camadas, \(\pmb{z}_1(W_1)\), \(\pmb{z}_2(W_2)\), \(\pmb{z}_3(W_3)\), \(\pmb{z}_4(W_4)\) e uma camada de saída \(\pmb{z}_o(W_o)\) e um custo \(\mathcal{L}\), para conseguir

usamos backpropagation para computar uma regra da cadeia que nos dê:

Intuitivamente, podemos ver que várias derivadas são multiplicadas acima. Como acontece com o processo de multiplicação, se essas derivadas forem maiores do que zero, o produto explode para um número muito grande; se a as derivas forem menores do que zero, o produto desvanece para um número muito próximo de zero. Isso leva ao que chamamos de Problema dos Gradientes Explodindo ou Desvanecendo de treinar redes neurais. Quando RNAs são muito profundas, a chance da regra da cadeia produzir uma multiplicação instável aumenta. Como consequência, a atualização dos parâmetros das camadas mais longe da saída tendem a sofrer atualizações instáveis, ou insignificantes (mais comum) ou muito grandes (mais raro). Logo, quanto mais profunda a rede neural, embora mais poderosa, também mais difícil será treiná-la.

As Primeiras Redes Neurais Artificiais

O modelo de RNA teve seu advento na década de 40, mas devido às dificuldades de treiná-las, só recentemente elas conseguiram fazer par e até superar sistematicamente outros modelos de aprendizado de máquina. Parte da recente popularização de Deep Learning se deu ao fato de que só agora conseguimos mitigar o problema do gradiente explodindo ou desvanecendo. Assim sendo, entender o que causa o produto instável que vimos acima assim como as técnicas para estabilizá-lo é fundamental para conseguir treinar redes neurais artificiais com sucesso.

Nos tutoriais passados, na redes neurais implementadas anteriormente, eu já usei algumas dessas técnicas sem mencioná-las diretamente. Por isso, neste tutorial vamos dar um passo atras e implementar uma rede neural profunda sem levar em conta as recentes descobertas e desenvolvimentos no campo de Deep Learning. O código será essencialmente o do tutorial de Redes Neurais Feedforward Densas, então não o colocarei todo aqui para evitar alongamentos e repetições. Caso queira olhá-lo inteiro, coloquei a versão completa no GitHub.

Essencialmente, vamos criar uma rede neural com 4 camadas ocultas e iniciar os pesos \(W_i\) segundo uma distribuição normal. Por exemplo, os parâmetros da primeira camada seriam criados com a seguinte linha:

W1 = tf.Variable(tf.random_normal([n_inputs, n_l1]))

OBS: anteriormente havíamos usado a função tf.truncated_normal() para iniciar os parâmetros. Essa função gera números aleatórios segundo uma normal, mas garantindo que eles nunca sejam muito distantes da média. A função tf.random_normal(...) não tem garantia.

Outra diferença é que as redes neurais antigas utilizavam a função sigmoide como não linearidade. Assim, as camadas da rede neural que criaremos aqui serão feitas como a seguir:

l1 = tf.nn.sigmoid(tf.matmul(x_input, W1) + b1)

OBS: anteriormente, havíamos usado a não linearidade ReLU, com tf.nn.relu(...).

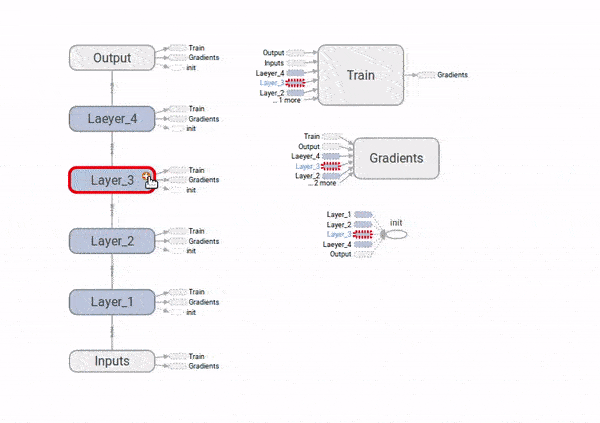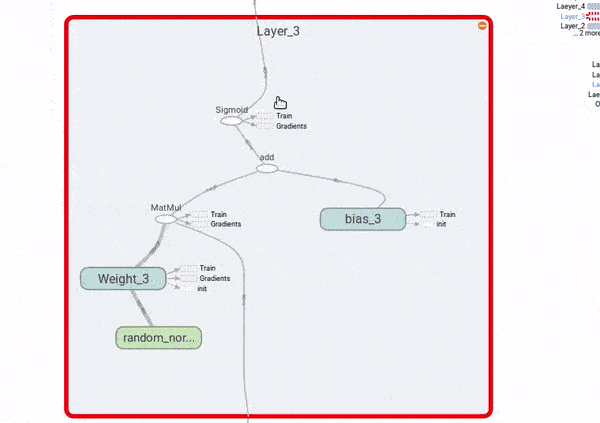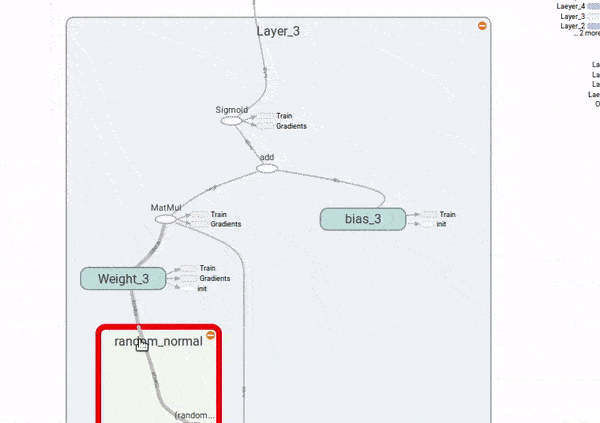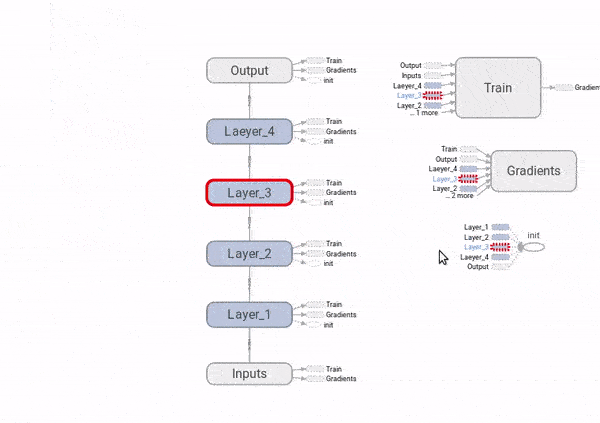
Finalmente, para ver como o problema dos gradientes explodindo ou desvanecendo, vamos adicionar ao gafo nós que computem as derivadas do custo com respeito aos \(W_i\). Também vamos colocar nós de resumo do TensorBoard, para visualizarmos as distribuições desses gradientes e poder compará-las ao longo das quatro camadas da rede neural.

# calcula as derivadas
de_dW1, de_dW2, de_dW3, de_dW4  = tf.gradients(error, [W1, W2, W3, W4])

# nós de resumo para o TensorBoard
tf.summary.histogram('Grads1', de_dW1)
tf.summary.histogram('Grads2', de_dW2)
tf.summary.histogram('Grads3', de_dW3)
tf.summary.histogram('Grads4', de_dW4)

Podemos usar a funcionalidade de autodiferenciação do TensorFlow para calcular as derivadas automaticamente. Isso é feito com a função tf.gradients(ys, [x1, ..., xn]), que calcula as derivadas do primeiro argumento com respeito ao segundo.

Resultados

Quando iniciamos o treinamento da rede neural descrita acima, na primeira iteração, os derivadas das quatro camadas apresentam as seguintes distribuições.

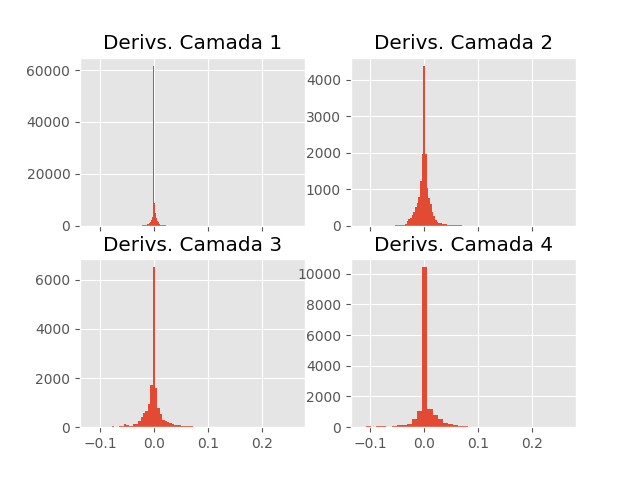
Como previsto, a distribuição dos derivadas da primeira camada é bastante centrado em zero, sendo que nem os extremos das caudas da distribuição chegam em \(\pm 0.025\). A medida que progredimos para camadas mais ao final da rede, a distribuição dos derivadas fica mais larga. Nesse caso, o problema da instabilidade dos derivadas faz com que os parâmetros da primeira sejam atualizados de maneira quase que insignificante, dificultando o seu treinamento.

Após algumas iterações de treino, a distribuição dos derivadas da primeira camada continuam próximos de zero. A distribuição das outras camadas também ficam mais centradas em zero, mas isso é esperado, conforme vimos no tutorial de gradiente descendente. Apenas relembrando, conforme o treinamento progride e vamos chegando em regiões de custo menor, onde a inclinação da superfície também é menor, diminuindo o gradiente. Assim, quanto mais avançado estiver o treinamento, menor tenderá a ser o gradiente. Isso só não será sempre verdade devido a não convexidade da superfície de custo das redes neurais.

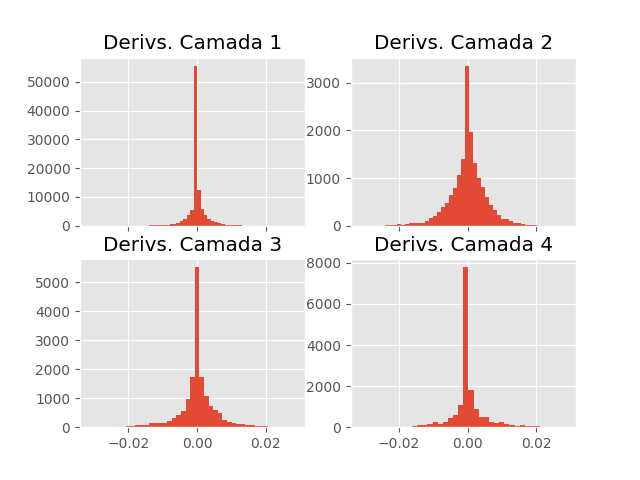
Nos próximos tutoriais, veremos algumas técnicas para mitigar o problema dos derivadas explodindo ou desvanecendo. Pelas mudanças que fizemos na rede neural aqui descrita relativamente as que havíamos implementado nos tutoriais passados, você já deve ter adivinhado sobre o que tratarão essas técnicas. Adiantando um pouco, dois métodos para lidar com a instabilidade dos derivadas envolvem mudanças na função de ativação (não linearidade) das camadas ocultas e mudanças na inicialização dos parâmetros.